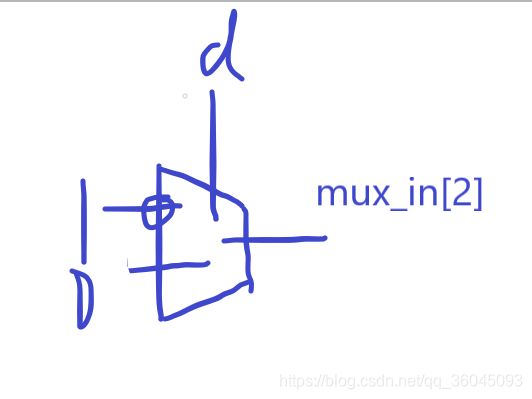Verilog HDL题库练习--题目来源HDLBits

写在开头：

HDLBits 上有很多Verilog HDL语言的题目，题目很有价值，有些题目也很有意思，让人脑洞打开。更重要的是，通过每道题目的铺垫以及层层递进的难度，让我对硬件电路有了更深刻的理解。因此我会在这篇文章里提取出一些有意思、有难度、也能引起思考的题目，分享给大家。btw，这是我第100篇博客，坚持到现在不容易，如果你能看到这里，请给我点个赞吧。个人能力有限，文章难免有多少错误，欢迎指正。

---

目录

一、Verilog HDL 语法

二、Combinational Logic Circuits组合逻辑电路

2.1 Basic Gates 基本门电路

2.2 Mutiplexers 多路选择器

1、2-to-1 multiplexer

2、2-to-1 bus multiplexer

3、9-to-1 multiplexer

4、256-to-1 multiplexer

5、256-to-1 4-bit multiplexer

2.3 Arithmetic Circuit 运算电路

2.3.1 Half adder

2.3.2 full adder 全加器 

2.3.3 3-bit binary adder 3位二进制加法器 

 2.3.4 Adder 加法器

 2.3.5 Signed addition overflow 有符号数的加法溢出检测

2.3.6 100-bit binary adder

2.3.7 4-digit BCD adder

2.4 Karnaugh Map to Circuit 电路的卡诺图描述

2.4.1 3-varible 3变量

2.4.2 4-variable 4变量

2.4.3 4-variable

2.4.4 4-variable

2.4.5 Minimum SOP and POS

2.4.6 Karnaugh Map

2.4.7  Karnaugh Map

2.4.8 K-map implemented with a multiplexer

三、Sequential Logic 时序逻辑电路

3.1 Latches and Flip-Flops 寄存器和触发器

3.1.1 D flip-flop D触发器

3.1.2 D flip-flops D触发器组合

3.1.3 DFF with reset 带复位的D触发器

3.1.4 DFF with reset value 带复位的D触发器

3.1.5 DFF with asynchromous reset 异步复位的DFF

3.1.6 DFF with byte enable 带使能位的DFF

3.1.7 D Latch D锁存器

3.1.8 DFF

3.1.9 DFF

3.1.10 DFF + gate

3.1.11 Mux and DFF

3.1.12 Mux and DFF

3.1.13 DFFs and gates

3.1.14 Create circuit from truth table

3.1.15 Detect an edge

3.1.16 Detect both edges

3.1.17 Edge capture register

3.1.18 Dual-edge triggered flip-flop

3.2 Counters 计数器

3.3 Shift Registers 移位寄存器

3.4 More Circuits

3.5 Finite State Machines 有限状态机

---

---

一、Verilog HDL 语法

二、Combinational Logic Circuits组合逻辑电路

2.1 Basic Gates 基本门电路

2.2 Mutiplexers 多路选择器

1、2-to-1 multiplexer

Create a one-bit wide, 2-to-1 multiplexer. When sel=0, choose a. When sel=1, choose b.

Expected solution length: Around 1 line.

 题目分析：用一行代码实现二选一选择器，那么就不能用if语句，这里选择条件运算符，也是唯一的三目运算符：<条件1>？<条件2>：<条件3>

它执行如下运算：在运算中，首先对第一个表达式进行检验，如果为真，则返回表达式2的值；如果为假，则返回表达式3的值。

再利用连续幅值语句assign，故所缺程序为：assign out = (sel) ? b : a;

module top_module( 
    input a, b, sel,
    output out ); 

    assign out = (sel) ? b : a;
endmodule

 当然，也可以对向量进行选择，这里不再赘述，直接提供程序：

2、2-to-1 bus multiplexer

module top_module( 
    input [99:0] a, b,
    input sel,
    output [99:0] out );

    assign out = (sel) ? b : a;
endmodule

3、9-to-1 multiplexer

Create a 16-bit wide, 9-to-1 multiplexer. sel=0 chooses a, sel=1 chooses b, etc. For the unused cases (sel=9 to 15), set all output bits to '1'.

Expected solution length: Around 15 lines.

题目分析：要求我们根据sel的值来对某一个输入直接输出。sel的情况较多，但是可以一一列举，因此选择case语句列举出所有情况，且新增程序没有超过15行。

直接给出完整程序：

module top_module( 
    input [15:0] a, b, c, d, e, f, g, h, i,
    input [3:0] sel,
    output [15:0] out );
    
    always@(*)
        begin
            case(sel)
                4'b0000: out = a;
                4'b0001: out = b;
                4'b0010: out = c;
                4'b0011: out = d;
                4'b0100: out = e;
                4'b0101: out = f;
                4'b0110: out = g;
                4'b0111: out = h;
                4'b1000: out = i;
                default:out = 16'hffff;
            endcase
        end
                  

endmodule

这里我们注意一下，Verilog数据常量的写法：

数字表达式：<位宽><进制><数字>
’b:二进制 //eg.4'b1110 表示4位二进制数1110
‘h:十六进制 //eg 8'hef、4’ha等
'd:十进制 //eg 2'd3、4‘d15(不能写16，4位宽最大15)等

计算位宽时，都要转成二进制来计算，因为时序元件只能存储二值电平。

4、256-to-1 multiplexer

前面几题都比较简单，一些小知识点写出来全当做复习了，后面两题会有点难度。

Create a 1-bit wide, 256-to-1 multiplexer. The 256 inputs are all packed into a single 256-bit input vector. sel=0 should select in[0], sel=1 selects bits in[1], sel=2 selects bits in[2], etc.

Expected solution length: Around 1 line.

Module Declaration

module top_module( 
    input [255:0] in,
    input [7:0] sel,
    output out );

题目分析：要求我们根据sel的值选择in的某一位输出，因为sel有8bit，因此有2^8=256种可能，正好填满了in中的所有位。

没有思路前可以先试着写前几个：

sel=0，out=in[0]；

sel = 1，out = in[1];

所以很明显，sel值就是要输出的in的下标，因此我们确实可以用1行代码来搞定它，直接给出完整程序：

module top_module( 
    input [255:0] in,
    input [7:0] sel,
    output out );

    assign out = in[sel];
endmodule

5、256-to-1 4-bit multiplexer

Create a 4-bit wide, 256-to-1 multiplexer. The 256 4-bit inputs are all packed into a single 1024-bit input vector. sel=0 should select bits in[3:0], sel=1 selects bits in[7:4], sel=2 selects bits in[11:8], etc.

Expected solution length: Around 1–5 lines.

Module Declaration

module top_module( 
    input [1023:0] in,
    input [7:0] sel,
    output [3:0] out );

 题目：上一题只能算小试身手，这题才是开胃大菜。要求我们根据sel的值，选择in的某连续4位进行输出，这里题目给了提示，我们也来康康：

• With this many options, a case statement isn't so useful.
• Vector indices can be variable, as long as the synthesizer can figure out that the width of the bits being selected is constant. It's not always good at this. An error saying "... is not a constant" means it couldn't prove that the select width is constant. In particular, in[ sel*4+3 : sel*4 ] does not work.
• Bit slicing ("Indexed vector part select", since Verilog-2001) has an even more compact syntax.

 提示分析：1、由于情况太多，case语句写起来太冗长了；

2、“向量索引是可以变化的”（意思是可以用变量来表示索引），但是后面又说“只要合成器能算出被选择位的宽度是恒定的”，否则编译器会报错。这句话翻译成人话就是：可以用变量来表示向量索引，但是编译器会因为无法识别出被选择位的宽度而报错，比如说in[ sel*4+3 : sel*4 ] 这个语句就不能用，因为其宽度没有直接指定。

3、可以使用“位切片”的方法来实现，只不过这是更高级的语法。

说了这么多，其实我们还不知道正确答案是什么，我们直接看网上的程序：

example1：

assign out = {in[sel * 4 + 3], in[sel * 4 + 2], in[sel * 4 + 1], in[sel * 4]};

这种写法很好地避免了被选择位宽度无法识别的问题，又使用了变量来表示索引，是比较容易理解的一种答案。作为学习，我们当然也得看看提示中说的更高级的解法啊。

example2:

assign out = in[sel*4 +: 4];

这句话的意思是：从sel*4开始，选择比特序号大于sel*4的4位bit，相当于[sel*4+3:sel*4]。这种写法应该是这题出题人的意图了，这种语法只在Verilog 2001适用：

在verilog-1995中，可以选择向量的任一位输出，也可以选择向量的连续几位输出，不过此时连续几位的始末数值的index需要是常量。而在Verilog-2001中，可以用变量作为index，进行part select。

[base_expr +: width_expr] //positive offset

[base_expr -: width_expr] //negative offset

其中base_expr可以是变量，而width_expr必须是常量。+：表示由base_expr向上增长width_expr位，-：表示由base_expr向上递减width_expr位。例如：

reg [63:0] word;

reg [3:0] byte_num; //a value from 0 to 7

wire [7:0] byteN = word[byte_num*8 +: 8];

如果byte_num的值为4，则word[39:32]赋值给byteN。

 example3:

有了上面的解释，第三种答案也就出来了：

assign out = in[sel*4+3-:4];

从sel*4+3开始，选择比特序号小于sel*4+3的4位bit，相当于[sel*4+3:sel*4]

总结一下答案如下：

module top_module( 
    input [1023:0] in,
    input [7:0] sel,
    output [3:0] out );
    
    assign out = {in[sel*4+3],in[sel*4+2],in[sel*4+1],in[sel*4]};//这种方式最直接、容易理解
    //assign out = = in[sel*4 +: 4];
    //assign out = in[sel*4+3-:4];

endmodule

2.3 Arithmetic Circuit 运算电路

2.3.1 Half adder

Create a half adder. A half adder adds two bits (with no carry-in) and produces a sum and carry-out.

Expected solution length: Around 2 lines.

题目分析：创建一个半加器（无低位进位） ，2行代码。

比较简单，直接po出程序

module top_module( 
    input a, b,
    output cout, sum );
    
    assign {cout,sum} = a + b; 

endmodule

2.3.2 full adder 全加器 

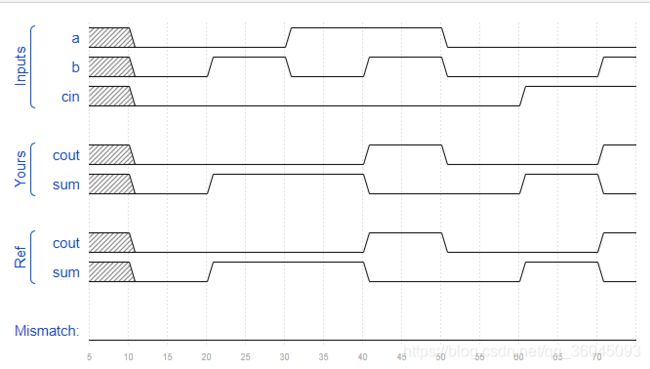
Create a full adder. A full adder adds three bits (including carry-in) and produces a sum and carry-out.

Expected solution length: Around 2 lines.

 题目分析：创建一个全加器（含低位进位）

与上题一样，直接给出程序：

module top_module( 
    input a, b, cin,
    output cout, sum );
    
    assign {cout,sum} = a + b +cin;

endmodule

2.3.3 3-bit binary adder 3位二进制加法器 

Now that you know how to build a full adder, make 3 instances of it to create a 3-bit binary ripple-carry adder. The adder adds two 3-bit numbers and a carry-in to produce a 3-bit sum and carry out. To encourage you to actually instantiate full adders, also output the carry-out from each full adder in the ripple-carry adder. cout[2] is the final carry-out from the last full adder, and is the carry-out you usually see.

Module Declaration

module top_module( 
    input [2:0] a, b,
    input cin,
    output [2:0] cout,
    output [2:0] sum );

 题目分析：利用3个一位全加器实现三位并行加法器

分析如下：

程序如下：

module top_module( 
    input [2:0] a, b,
    input cin,
    output [2:0] cout,
    output [2:0] sum );
    
    fadder U1(a[0],b[0],cin,cout[0],sum[0]);
    fadder U2(a[1],b[1],cout[0],cout[1],sum[1]);
    fadder U3(a[2],b[2],cout[1],cout[2],sum[2]);

endmodule

module fadder(
     input a, b, cin,
    output cout, sum );
    
    assign {cout,sum} = a + b +cin;

endmodule

 2.3.4 Adder 加法器

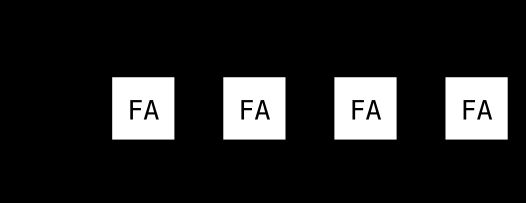
Implement the following circuit:

("FA" is a full adder)

题目分析：跟上一题有所不同，进位位由最高的cout的输出，其余低位的cout作为高位的cin，最低的全加器的cin为0

module top_module (
    input [3:0] x,
    input [3:0] y, 
    output [4:0] sum);

    wire w1,w2,w3;
	fadder U1(x[0],y[0],1'b0,w1,sum[0]);
	fadder U2(x[1],y[1],w1,w2,sum[1]);
    fadder U3(x[2],y[2],w2,w3,sum[2]);
    fadder U4(x[3],y[3],w3,sum[4],sum[3]);
    
endmodule
	


module fadder(
	input a, b, cin,
    output cout, sum);
    
    assign {cout,sum} = a + b +cin;
endmodule

 2.3.5 Signed addition overflow 有符号数的加法溢出检测

Assume that you have two 8-bit 2's complement numbers, a[7:0] and b[7:0]. These numbers are added to produce s[7:0]. Also compute whether a (signed) overflow has occurred.

Module Declaration

module top_module (
    input [7:0] a,
    input [7:0] b,
    output [7:0] s,
    output overflow
); 

题目分析：判断两个数相加的结果有无溢出

Hint...

A signed overflow occurs when adding two positive numbers produces a negative result, or adding two negative numbers produces a positive result. There are several methods to detect overflow: It could be computed by comparing the signs of the input and output numbers, or derived from the carry-out of bit n and n-1.

提示翻译：当两个正数相加产生一个负数，或两个负数相加产生一个正数时，就会发生有符号数的溢出。

可以通过比较输入和输出数的符号来计算溢出。从位n和n-1的进位推导出来。

提示分析：我们知道计算机是用二进制补码进行加法运算的，包括正数与负数，为了更好地理解溢出的情况，我们举两个例子：

十进制：-7-5=-12

二进制（4位二进制，最高位为符号位）: -7 =1111（原码），-7 = 1000（反码：-7的绝对值0111按位取反），-7=1001（补码：反码+1）

-5 = 1101（原码），-5 = 1010（反码：原码除符号位按位取反），-5 = 1011（补码）

    1001

+  1011

=10100（补码）

发现结果是0100，即+4，这是因为4位二进制的最高位本来是用来表示符号的（也即有符号数），现在被低位进位填充了，丢失了符号位，导致计算结果由负变正。

我们再举一个例子，4位二进制有符号数的范围为-7到+7，如果和的结果大于这个数，也会导致溢出，比如（+4）+（+5）=+9。注意：正数的原码、反码、补码是一样的

+4=0100；+5=0101；

     0100

+   0101

= 01001

我们看到结果变成了负数，原因也是和的结果把符号位占据了，丢失了符号数据。

通过上面两个例子，再结合提示所说的两种方法，我们有了如下思路：

法①：比较和s的最高位与两个加数a、b的最高位，是否相同，若相同则无溢出，若不同则溢出；注意：如果两个加数的符号不同（正数+负数），和的结果肯定不会溢出。

a[7]	b[7]	s[7]	overflow
0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	0
1	0	0	0
1	0	1	0
1	1	0	1
1	1	1	0

 

那么：overflow = ~a[7]&~b[7]&s[7] + a[7]&b[7]&~s[7]

module top_module (
    input [7:0] a,
    input [7:0] b,
    output [7:0] s,
    output overflow
); //
    
    // assign s = ...
    // assign overflow = ...
    assign s = a + b;
    assign overflow = ~a[7]&~b[7]&s[7] | a[7]&b[7]&~s[7];

endmodule

2.3.6 100-bit binary adder

Create a 100-bit binary adder. The adder adds two 100-bit numbers and a carry-in to produce a 100-bit sum and carry out.

Expected solution length: Around 1 line.

Module Declaration

module top_module( 
    input [99:0] a, b,
    input cin,
    output cout,
    output [99:0] sum );

使用一行代码实现：

module top_module( 
    input [99:0] a, b,
    input cin,
    output cout,
    output [99:0] sum );
    
    assign {cout,sum} = a + b + cin;

endmodule

2.3.7 4-digit BCD adder

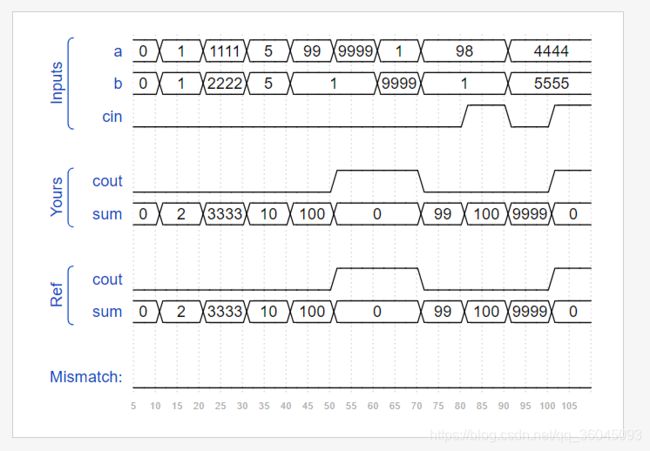
You are provided with a BCD (binary-coded decimal) one-digit adder named bcd_fadd that adds two BCD digits and carry-in, and produces a sum and carry-out.

module bcd_fadd {
    input [3:0] a,
    input [3:0] b,
    input     cin,
    output   cout,
    output [3:0] sum );

Instantiate 4 copies of bcd_fadd to create a 4-digit BCD ripple-carry adder. Your adder should add two 4-digit BCD numbers (packed into 16-bit vectors) and a carry-in to produce a 4-digit sum and carry out.

Module Declaration

module top_module( 
    input [15:0] a, b,
    input cin,
    output cout,
    output [15:0] sum );

题目分析： 利用4位BCD加法器构建16位BCD加法器，BCD：二-十进制

• The BCD representation for the 5-digit decimal number 12345 is 20'h12345. This is not the same as 14'd12345 (which is 14'h3039).
• The circuit is structured just like a binary ripple-carry adder, except the adders are base-10 rather than base-2.

提示分析：

5位十进制数12345的BCD码的表示是20'h12345。这和14'd12345 (14'h3039)不一样。

该电路的结构就像二进制并行进位加法器，除了加法器是基10而不是基2。

 模块连接方法跟之前一样，低位的cout给到高位的cin

module top_module( 
    input [15:0] a, b,
    input cin,
    output cout,
    output [15:0] sum );
    
    wire w1,w2,w3;
    bcd_fadd U1(a[3:0],b[3:0],cin,w1,sum[3:0]);
    bcd_fadd U2(a[7:3],b[7:3],w1,w2,sum[7:3]);
    bcd_fadd U3(a[11:8],b[11:8],w2,w3,sum[11:8]);
    bcd_fadd U4(a[15:12],b[15:12],w3,cout,sum[15:12]);

endmodule

区别：之前是二进制加法（满2进1），现在是十进制加法器

2.4 Karnaugh Map to Circuit 电路的卡诺图描述

2.4.1 3-varible 3变量

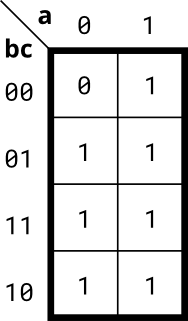
Implement the circuit described by the Karnaugh map below.

Try to simplify the k-map before coding it. Try both product-of-sums and sum-of-products forms. We can't check whether you have the optimal simplification of the k-map. But we can check if your reduction is equivalent, and we can check whether you can translate a k-map into a circuit.

题目分析：用电路图来描述该卡诺图

描述输出：可以直接用与门+或门实现，如out = b + c + a*(~b)*(~c);

也可以先表示出~out = ~a*~b&*~c，那么out = ~(~out) = ~(~a*~b&*~c);

module top_module(//方法一：直接表示
    input a,
    input b,
    input c,
    output out  ); 
    
    assign out = b | c | a&(~b)&(~c);

endmodule

 

module top_module(//方法二：表示其反变量
    input a,
    input b,
    input c,
    output out  ); 
    
    assign out = ~(~a&~b&~c);

endmodule

2.4.2 4-variable 4变量

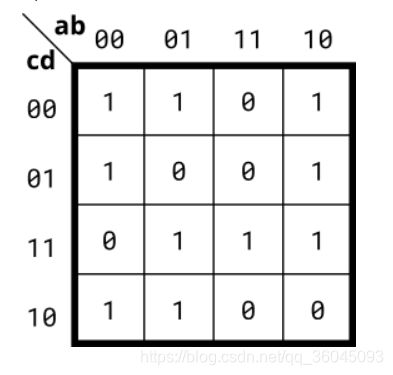
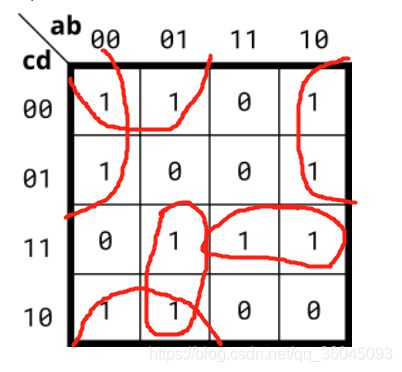
Implement the circuit described by the Karnaugh map below.

 

Try to simplify the k-map before coding it. Try both product-of-sums and sum-of-products forms. We can't check whether you have the optimal simplification of the k-map. But we can check if your reduction is equivalent, and we can check whether you can translate a k-map into a circuit.

题目分析：化简卡诺图，并用电路描述输出与输入的关系

 

out = ~a & ~d | ~b & ~c | a & c & d | ~a & b & c; 

module top_module(
    input a,
    input b,
    input c,
    input d,
    output out  ); 
    //直接描述输出：通过找几何相邻（逻辑相邻），再画圆来合并最小项
    assign out = ~a & ~d | ~b & ~c | a & c & d | ~a& b & c;

endmodule

2.4.3 4-variable

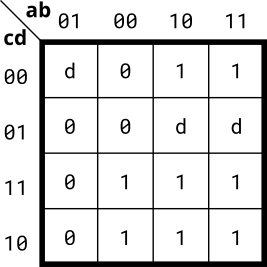
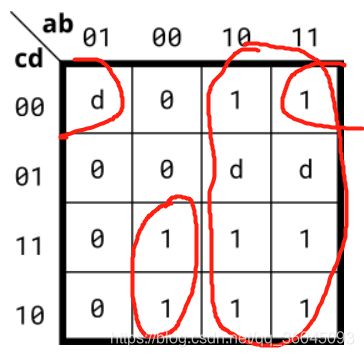
Implement the circuit described by the Karnaugh map below.

Try to simplify the k-map before coding it. Try both product-of-sums and sum-of-products forms. We can't check whether you have the optimal simplification of the k-map. But we can check if your reduction is equivalent, and we can check whether you can translate a k-map into a circuit.

题目分析：卡诺图中出现了d，d的意思就是不关系，也即do not care的意思。 相当于无关项，可为1也可以为0，通常用x表示。把有利于化简的d看做1，否则为0比较能够化简出最简的表达式：

把d看成1：

out  = a  | b & ~c & ~d | ~a & ~b & c;

把d看成0： 

out = a |  ~b & c;

module top_module(
    input a,
    input b,
    input c,
    input d,
    output out  ); 
    //把d看成0
    assign out = a | ~b & c;

endmodule

2.4.4 4-variable

Implement the circuit described by the Karnaugh map below.

Try to simplify the k-map before coding it. Try both product-of-sums and sum-of-products forms. We can't check whether you have the optimal simplification of the k-map. But we can check if your reduction is equivalent, and we can check whether you can translate a k-map into a circuit. 

 题目分析：卡诺图变成了0、1相邻排列，几何相邻不成立了，无法用与或表达式方便地表示了。

Hint...

For this function, changing the value of any one input always inverts the output. It is a simple logic function, but one that can't be easily expressed as SOP nor POS forms.

提示分析：对于这个函数，改变任何一个输入的值总是与输出相反。它是一个简单的逻辑函数，但不能简单地表示为SOP（乘积的和）或POS（和的乘积）形式。 

异或：如果两数相异结果为1，多个数中：如果出现奇数个1结果为1、偶数个1为0。

module top_module(
    input a,
    input b,
    input c,
    input d,
    output out  ); 
    
    assign out = a ^ b ^ c ^d;

endmodule

2.4.5 Minimum SOP and POS

A single-output digital system with four inputs (a,b,c,d) generates a logic-1 when 2, 7, or 15 appears on the inputs, and a logic-0 when 0, 1, 4, 5, 6, 9, 10, 13, or 14 appears. The input conditions for the numbers 3, 8, 11, and 12 never occur in this system. For example, 7 corresponds to a,b,c,d being set to 0,1,1,1, respectively.

Determine the output out_sop in minimum SOP form, and the output out_pos in minimum POS form.

Module Declaration

module top_module (
    input a,
    input b,
    input c,
    input d,
    output out_sop,
    output out_pos
); 

SOP（乘积的和），即化成最小项的形式，也就是圈1和doncare项；

POS（和的乘积），即化成最大项的形式，也就是圈0和doncare项之后，整体取反，再根据德摩根律化简即可。

先求SOP：

out_sop = c & d | ~a & ~b & c;

再求POS：

 out_pos = ~(~c | ~a & b & ~d | a & ~d);

module top_module (
    input a,
    input b,
    input c,
    input d,
    output out_sop,
    output out_pos
); 
    assign out_sop = c & d | ~a & ~b & c;
    assign out_pos = ~(~c | ~a & b & ~d | a & ~d);

endmodule

2.4.6 Karnaugh Map

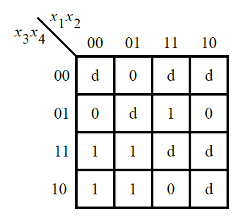
Consider the function f shown in the Karnaugh map below.

Implement this function. d is don't-care, which means you may choose to output whatever value is convenient.

题目分析：函数功能实现

f = x3 & x4 | ~x1 & x3 | x1 & x2 & x4; 

module top_module (
    input [4:1] x, 
    output f );
    
    assign f = x[3] & x[4] | ~x[1] & x[3] | x[1] & x[2] & x[4];

endmodule

2.4.7  Karnaugh Map

Consider the function f shown in the Karnaugh map below. Implement this function.

(The original exam question asked for simplified SOP and POS forms of the function.)

 

 f = ~x1 & x3 | x2 & x3 & x4 | x1 & ~x2 & ~x4 | ~x1 & ~x2 & ~x4;

module top_module (
    input [4:1] x,
    output f
); 
    
    assign f = ~x[1] & x[3] | x[2] & x[3] & x[4] | x[1] & ~x[2] & ~x[4] | ~x[1] & ~x[2] & ~x[4];

endmodule

2.4.8 K-map implemented with a multiplexer

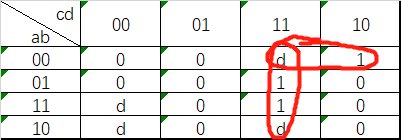
For the following Karnaugh map, give the circuit implementation using one 4-to-1 multiplexer and as many 2-to-1 multiplexers as required, but using as few as possible. You are not allowed to use any other logic gate and you must use a and b as the multiplexer selector inputs, as shown on the 4-to-1 multiplexer below.

You are implementing just the portion labelled top_module, such that the entire circuit (including the 4-to-1 mux) implements the K-map.

(The requirement to use only 2-to-1 multiplexers exists because the original exam question also wanted to test logic function simplification using K-maps and how to synthesize logic functions using only multiplexers with constant inputs. If you wish to treat this as purely a Verilog exercise, you may ignore this constraint and write the module any way you wish.)

Module Declaration

module top_module (
    input c,
    input d,
    output [3:0] mux_in
); 

题目翻译：

对于下面的卡诺图，给出使用一个4对1多路复用器和一些2对1多路复用器的电路实现，但使用尽可能少。

你不允许使用任何其他逻辑门，你必须使用a和b作为多路转换器选择输入，如下面的4对1多路转换器所示。

您只实现了标记为top_module的部分，这样整个电路(包括4对1 mux)就实现了K-map。

(只使用2对1多路复用器的要求是存在的，因为最初的考试题目还想测试使用k -map的逻辑函数简化，以及如何仅使用常量输入的多路复用器来合成逻辑函数。如果您希望将此视为纯粹的Verilog练习，您可以忽略此约束，并以您希望的任何方式编写模块。)

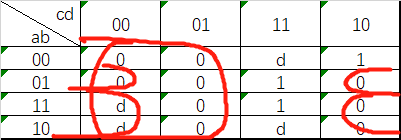
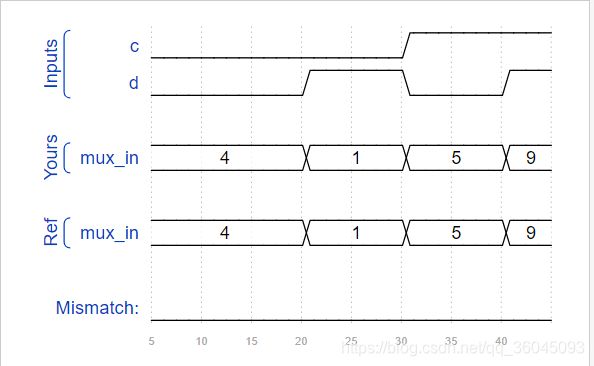
 题目分析：输入c，d，输出4位mux_in信号，在多路选择器的控制下，实现卡诺图的逻辑功能。

f = a & ~b & ~d | ~a & ~b & d | ~a & ~b & c | a & b & c & d;

a,b = 0,0   →   f = c | d  →  mux_in[0] = c | d;

a,b = 0,1   →   f = 0 →  mux_in[1] = 0;

a,b = 1,0   →   f = ~ d  →  mux_in[2] = ~d;

a,b = 1,1   →   f = c & d  →  mux_in[3] = c & d;

使用逻辑门的方法：

module top_module (
    input c,
    input d,
    output [3:0] mux_in
); 
    
    assign mux_in[0] = c | d;
    assign mux_in[1] = 1'b0;
    assign mux_in[2] = ~d;
    assign mux_in[3] = c & d;

endmodule

但上述方法，很明显不符合题目要求，如何仅使用二选一数据选择权来实现呢？

首先肯定上述赋值逻辑是正确的，只不过结果是通过逻辑门实现的，而不是二选一选择器，只需要换种逻辑描述方式就行了：

mux_in[0] = c | d; 换成 mux_in[0] = (c ? 1 : (d ? 1 : 0));如果c为1，结果为1，否则，当d为1，结果为1；
mux_in[1] = 1'b0; 没有使用逻辑门，不用变 
mux_in[2] = ~d; 换成 mux_in[2] = d ? 0 : 1; d为1时取0，否则取1；
mux_in[3] = c & d; 换成 mux_in[3] =  c ? (d ? 1 : 0) : 0; c为1时取d值，且d为1，结果才为1；

module top_module (
    input c,
    input d,
    output [3:0] mux_in
); 
    
    assign mux_in[0] = (c ? 1 : (d ? 1 : 0));
    assign mux_in[1] = 1'b0;
    assign mux_in[2] = d ? 0 : 1;
    assign mux_in[3] = c ? (d ? 1 : 0) : 0;

endmodule

 

三、Sequential Logic 时序逻辑电路

3.1 Latches and Flip-Flops 寄存器和触发器

3.1.1 D flip-flop D触发器

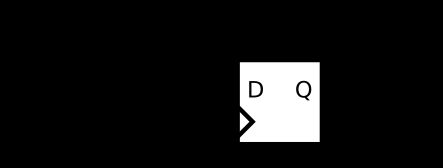
module top_module (
    input clk,    // Clocks are used in sequential circuits
    input d,
    output reg q );//
    always@(posedge clk)
	q <= d;
    // Use a clocked always block
    //   copy d to q at every positive edge of clk
    //   Clocked always blocks should use non-blocking assignments

endmodule

3.1.2 D flip-flops D触发器

module top_module (
    input clk,
    input [7:0] d,
    output [7:0] q
);

    always @(posedge clk)
        q <= d;
endmodule

3.1.3 DFF with reset 带同步复位的D触发器

module top_module (
    input clk,
    input reset,            // Synchronous reset
    input [7:0] d,
    output [7:0] q
);
    always@(posedge clk)
        begin
            if(reset ==1)
                q <=0;
            else
                q <=d;
        end

endmodule

3.1.4 DFF with reset value 带复位的D触发器

module top_module (
    input clk,
    input reset,
    input [7:0] d,
    output [7:0] q
);
    always @(negedge clk)
        begin
            if(reset == 1)
                q <= 'h34;
            else
                q <=d;
        end

endmodule

3.1.5 DFF with asynchromous reset 异步复位的DFF

module top_module (
    input clk,
    input areset,   // active high asynchronous reset
    input [7:0] d,
    output [7:0] q
);
    always @(posedge clk,posedge areset)
        begin
            if(areset)
                q <= 0;
            else
                q <=d;
        end
    

endmodule

3.1.6 DFF with byte enable 带使能位的DFF

module top_module (
    input clk,
    input resetn,
    input [1:0] byteena,
    input [15:0] d,
    output [15:0] q
);
    always@(posedge clk)
        begin
            if(!resetn)
                q<=0;
            else
                case(byteena)
                    2'b11:q<=d;
                   	2'b10:q[15:8]<=d[15:8];
                    2'b01:q[7:0]<=d[7:0];
                    default:q<=q;
                endcase
      
        end
endmodule

3.1.7 D Latch D锁存器

module top_module (
    input d, 
    input ena,
    output q);
    
    always@(*)
        begin
            if(ena)
                q <= d;
            else
                q <=q;
        end

endmodule

3.1.8 DFF

module top_module (
    input clk,
    input d, 
    input ar,   // asynchronous reset
    output q);
	
    always @(posedge clk or posedge ar)
        begin
            if(ar)
                q<=0;
            else
                q<=d;
        end
endmodule

3.1.9 DFF

module top_module (
    input clk,
    input d, 
    input r,   // synchronous reset
    output q);

    always@(posedge clk)
        begin
			if(r)
            	q<=0;
   	 		else
        		q<=d;
    	end
            
endmodule

3.1.10 DFF + gate

module top_module (
    input clk,
    input in, 
    output out);

    always@(posedge clk)
        out <= in ^ out;
endmodule

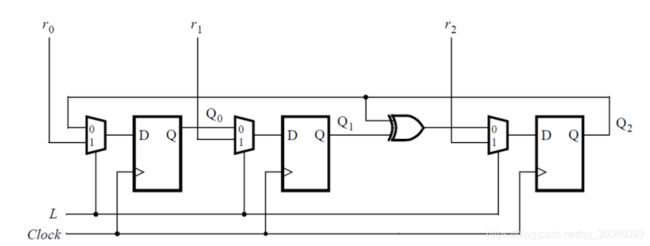
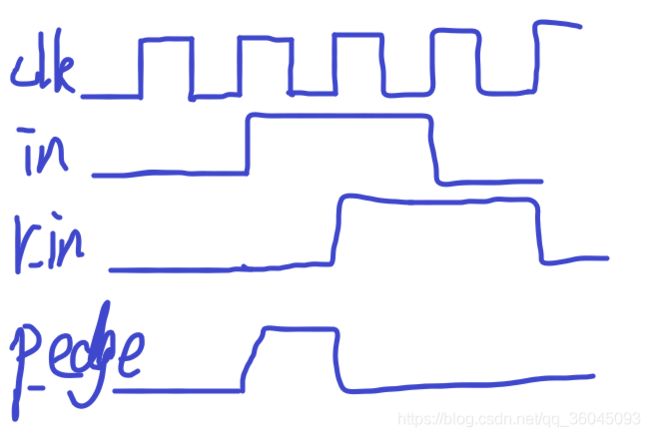
3.1.11 Mux and DFF

module top_module (
	input clk,
	input L,
	input r_in,
	input q_in,
	output reg Q);

    always@(posedge clk)
        begin 
            if(L==0)
                Q<=q_in;
        	else
                Q<=r_in;
        end
endmodule

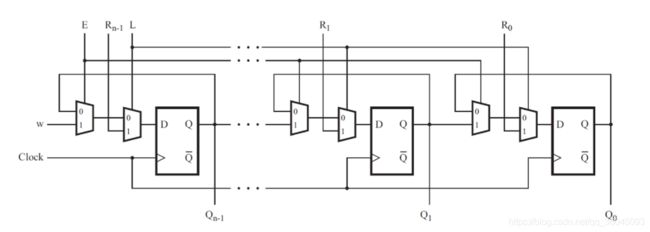
3.1.12 Mux and DFF

module top_module (
    input clk,
    input w, R, E, L,
    output Q
);

    always@(posedge clk)
        begin
            if(L)
                Q<=R;
            else if(E==0)
                Q<=Q;
            else 
                Q<=w;
                
        end
    
endmodule

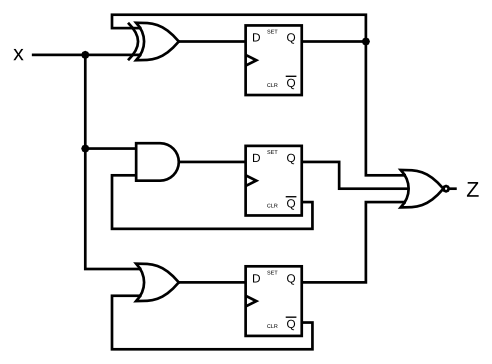
3.1.13 DFFs and gates

module top_module (
    input clk,
    input x,
    output z
); 
    reg q1,q2,q3;
    always@(posedge clk)
        begin
            q1<=x^q1;
            q2<=x&(!q2);
            q3<=x|(!q3);
        end
     assign z = !(q1|q2|q3);

endmodule

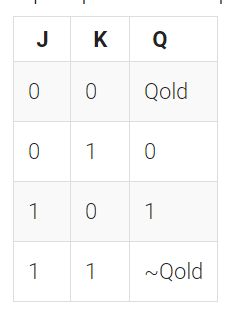
3.1.14 Create circuit from truth table JK触发器

module top_module (
    input clk,
    input j,
    input k,
    output Q); 

    always @(posedge clk)
        begin
            case({j,k})
                2'b00:Q<=Q;
                2'b01:Q<=0;
                2'b10:Q<=1;
                default:Q<=~Q;
            endcase
        end
endmodule

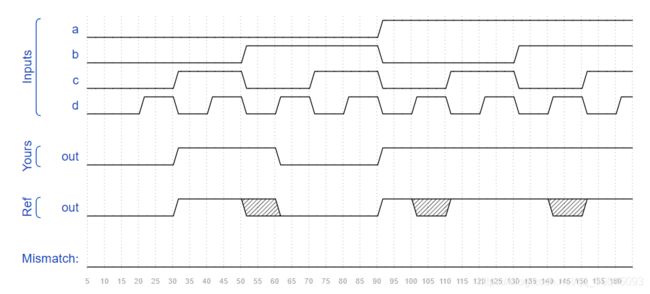
3.1.15 Detect an edge

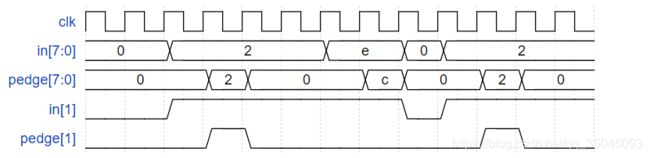
For each bit in an 8-bit vector, detect when the input signal changes from 0 in one clock cycle to 1 the next (similar to positive edge detection). The output bit should be set the cycle after a 0 to 1 transition occurs.

Here are some examples. For clarity, in[1] and pedge[1] are shown separately.

Module Declaration

module top_module (
    input clk,
    input [7:0] in,
    output [7:0] pedge
);

题目分析： 8位输入信号某位由0上升为1时，输出的对应位为1，仅持续一个周期

module top_module (
    input clk,
    input [7:0] in,
    output [7:0] pedge
);

    reg [7:0] reg_in;
    always@(posedge clk)
        reg_in <= in;
    
    always@(posedge clk)
        pedge <= ~reg_in & in;
    
endmodule

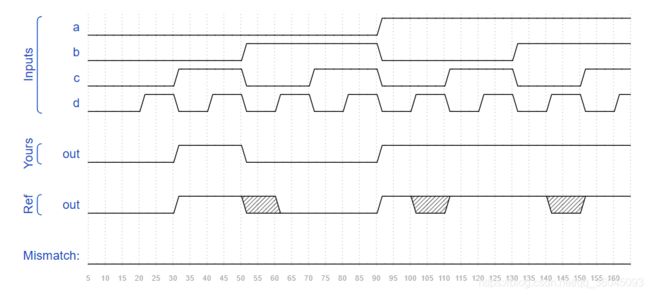
3.1.16 Detect both edges

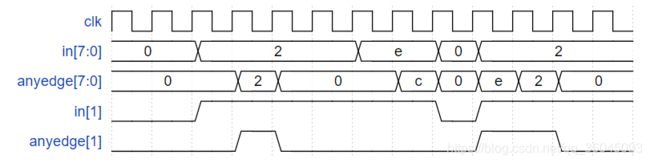
For each bit in an 8-bit vector, detect when the input signal changes from one clock cycle to the next (detect any edge). The output bit should be set the cycle after a 0 to 1 transition occurs.

Here are some examples. For clarity, in[1] and anyedge[1] are shown separately

 题目分析：上题是上升沿检测，本题是双边沿检测。

 

3.1.17 Edge capture register

3.1.18 Dual-edge triggered flip-flop

3.2 Counters 计数器

3.3 Shift Registers 移位寄存器

3.4 More Circuits

3.5 Finite State Machines 有限状态机