自学SLAM（5）《第三讲：李群和李代数》作业

前言

小编研究生的研究方向是视觉SLAM，目前在自学，本篇文章为初学高翔老师课的第三次作业。

---

1.群的性质

课上我们讲解了什么是群。请根据群定义，求解以下问题：

1. {Z, +} 是否为群？若是，验证其满⾜群定义；若不是，说明理由。
2. {N, +} 是否为群？若是，验证其满⾜群定义；若不是，说明理由。
   其中 Z 为整数集， N 为⾃然数集。

在这里我再写一下群的定义，满足“凤姐咬你”的就是群，也就是四个性质，如图：
注意：
Ⅰ 图中吧集合记作A，运算记作·（·不代表乘法），群可以记作G=(A,·)
Ⅱ 对于整数的逆，进行的是乘法，它的逆就是它的倒数 进行的是加法，它的逆就是它的相反数

对于 {Z, +} ，设a₁∈Z，a₂∈Z，a₃∈Z
①封闭性：对于任意的a₁∈Z，a₂∈Z都有a₁+a₂∈Z，满足封闭性。
②结合性：对于任意的a₁∈Z，a₂∈Z，a₃∈Z，都有（a₁+a₂）+a₃=a₁+（a₂+a₃），满足结合性。
③幺元：Z中存在0∈Z，对于任意的a∈Z，有a+0=a+0=a，因此满足幺元。
④逆：对于任意的a∈Z，有-a∈Z,a+(-a)=0，任何整数加上它的相反数等于幺元0，所以逆元素是其相反数，因此满足逆。

对于 {N, +}
①封闭性：两个自然数相加依然是自然数，封闭性成立。
②结合性：两个自然数相加可以互换位置，结合性成立。
③幺元：任何自然数与0相加仍然是自然数本身，幺元成立。
④逆: 自然数都是非负数（加法中，自然数的逆已经不属于自然数了），所以两个大于等于0的数相加不可能为0，逆不成立。

2.验证向量叉乘的李代数性质

我们说向量和叉乘运算构成了李代数，现在请你验证它。书中对李代数的定义为：李代数由⼀个集合V，⼀个数域 F 和⼀个⼆元运算 [，]组成。如果它们满⾜以下⼏条性质，称 (V， F， [， ]) 为⼀个李代数，记作g。
注意：自反性是指自己与自己的运算为零。

解题过程如下：

3.推导 SE(3) 的指数映射

课上给出了 SO(3) 的指数映射推导，但对于 SE(3)，仅介绍了结论，没有给出详细推导。请你完成 SE(3)指数映射部分，有关左雅可⽐的详细推导。

解题过程如下：

4.伴随

在 SO(3) 和 SE(3) 上，有⼀个东西称为伴随（Adjoint）。下⾯请你证明 SO(3)伴随的性质。

解题过程如下：

完整的 SO(3) 和 SE(3) 性质见下图

5.轨迹的描绘

我们通常会记录机器⼈的运动轨迹，来观察它的运动是否符合预期。⼤部分数据集都会提供标准轨迹以供参考，如 kitti、 TUM-RGBD 等。这些⽂件会有各⾃的格式，但⾸先你要理解它的内容。记世界坐标系为 W，机器⼈坐标系为 C，那么机器⼈的运动可以⽤ T_WC 或T_CW来描述。现在，我们希望画出机器⼈在世界当中的运动轨迹，请回答以下问题：

解题过程如下：
世界坐标系W(world)，机器人坐标系也就是相机坐标系C(camera)

①T_wc指的是从世界坐标系原点到相机中心的平移向量，(机器人(相机)坐标系的原点在世界坐标系中的坐标)
世界坐标系是不随相机运动变化的，因此可以认为T_wc是机器人相对于原点坐标在移动, 移动可视化在观察者眼中就是机器人的运动轨迹。

如果我们假设机器人坐标系的原点为O_c,此时的O_w就是这个原点在世界坐标系下的坐标：
O_w=T_wcO_c=t_wc
这正是T_wc的平移部分。因此，可以从T_wc中直接看到相机在何处，这也就是我们所说的T_wc更为直观。因此在可视化程序里，轨迹文件储存的是T_wc而不是T_cw。

我想这也是第一问问我们T_wc而不是问·T_cw的原因。

②
首先我们需要安装Sophus

    git clone https://github.com/strasdat/Sophus.git
    cd Sophus
    git checkout a621ff
    mkdir build
    cd build
    cmake ..
    make
    sudo make install

但是我们会编译失败，按照如下操作修改后，重新编译即可。
解决方法：打开 Sophus/sophus/so2.cpp文件修改报错内容

//将
SO2::SO2() 
{ 
 unit_complex_.real() = 1.; 
 unit_complex_.imag() = 0.; 
 }
//改为
SO2::SO2() 
{ 
   unit_complex_.real(1.); 
   unit_complex_.imag(0.); 
 }

这时候我们就可以安装成功Sophus了

draw_trajectory.cpp对应代码如下：

#include "sophus/so3.h"
#include "sophus/se3.h"
#include 
#include 
#include 
#include 
#include 
// need pangolin for plotting trajectory
#include 
using namespace std;
// path to trajectory file
string trajectory_file = "/home/zhe/1/lianxi/3/plotTrajectory/trajectory.txt";
class SE3d;
void DrawTrajectory(vector<Sophus::SE3, Eigen::aligned_allocator<Sophus::SE3>>);
int main(int argc, char **argv) {
    vector<Sophus::SE3, Eigen::aligned_allocator<Sophus::SE3>> poses;
    //文件读取器
    ifstream fin(trajectory_file);
    if (!fin) {
        cerr << "trajectory " << trajectory_file << " not found." << endl;
    }
    //如果eof()返回0，就没读完
    while (!fin.eof()) {
        //按照时间  平移 四元素的顺序定义并读取
        double time, tx, ty, tz, qx, qy, qz, qw;
        fin >> time >> tx >> ty >> tz >> qx >> qy >> qz >> qw;
        Sophus::SE3 p1(Eigen::Quaterniond(qw, qx, qy, qz), Eigen::Vector3d(tx, ty, tz));
        poses.push_back(p1);
    }
    fin.close();
    // end your code here
    // draw trajectory in pangolin
    DrawTrajectory(poses);
    return 0;
}
/************************************************************************/
void DrawTrajectory(vector<Sophus::SE3, Eigen::aligned_allocator<Sophus::SE3>> poses) {
    if (poses.empty()) {
        cerr << "Trajectory is empty!" << endl;
        return;
    }
    // create pangolin window and plot the trajectory
    pangolin::CreateWindowAndBind("Trajectory Viewer", 1024, 768);
    glEnable(GL_DEPTH_TEST);
    glEnable(GL_BLEND);
    glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);
    pangolin::OpenGlRenderState s_cam(
            pangolin::ProjectionMatrix(1024, 768, 500, 500, 512, 389, 0.1, 1000),
            pangolin::ModelViewLookAt(0, -0.1, -1.8, 0, 0, 0, 0.0, -1.0, 0.0)
    );
    pangolin::View &d_cam = pangolin::CreateDisplay()
            .SetBounds(0.0, 1.0, pangolin::Attach::Pix(175), 1.0, -1024.0f / 768.0f)
            .SetHandler(new pangolin::Handler3D(s_cam));
    while (pangolin::ShouldQuit() == false) {
        glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
        d_cam.Activate(s_cam);
        glClearColor(1.0f, 1.0f, 1.0f, 1.0f);
        glLineWidth(2);
        for (size_t i = 0; i < poses.size() - 1; i++) {
            glColor3f(1 - (float) i / poses.size(), 0.0f, (float) i / poses.size());
            glBegin(GL_LINES);
            auto p1 = poses[i], p2 = poses[i + 1];
            glVertex3d(p1.translation()[0], p1.translation()[1], p1.translation()[2]);
            glVertex3d(p2.translation()[0], p2.translation()[1], p2.translation()[2]);
            glEnd();
        }
        pangolin::FinishFrame();
        usleep(5000);   // sleep 5 ms
    }
}

CmakeLists.txt对应代码如下：

cmake_minimum_required(VERSION 2.8)
project(draw_trajectory)
set( CMAKE_BUILD_TYPE "Release" )
set( CMAKE_CXX_FLAGS "-std=c++11 -O3" )
set( CMAKE_BUILD_TYPE "Debug" )

find_package(Pangolin REQUIRED)
find_package(Sophus REQUIRED)
include_directories("/usr/include/eigen3")
include_directories(
        ${Pangolin_INCLUDE_DIRS}
        ${Sophus_INCLUDE_DIR}
)
add_executable(trajectory draw_trajectory.cpp)
target_link_libraries(trajectory
        ${Pangolin_LIBRARIES}
        ${Sophus_LIBRARIES}
        )

然后

cd  SLAM4track//自己建的文件夹
cat CMakeLists.txt
cd build
cmake ..
make
./trajectory

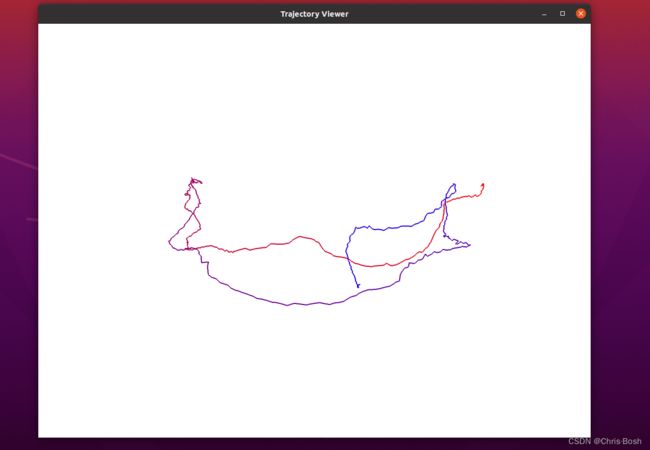
该图中:轨迹首尾颜色不一样,通过观察,发现是着色函数设置的颜色随位置变化.

6.* 轨迹的误差(附加题)

本题为附加题。 除了画出真实轨迹以外，我们经常需要把 SLAM 估计的轨迹与真实轨迹相⽐较。下⾯说明⽐较的原理，请你完成⽐较部分的代码实现。

CMakeLists.txt对应代码

cmake_minimum_required(VERSION 2.8)
project(wucha)

set(CMAKE_CXX_FLAGS "${CMAKE_CXX_FLAGS} -std=c++11")

#set(CMAKE_CXX_STANDARD 11)
#set(CMAKE_BUILD_TYPE "Release")
#set(CMAKE_RUNTIME_OUTPUT_DIRECTORY ${PROJECT_SOURCE_DIR}/bin)
#set(CMAKE_LIBRARY_OUTPUT_DIRECTORY ${PROJECT_SOURCE_DIR}/lib)
#添加库
#sophus
#  为使用 sophus，需要使用find_package命令找到它并赋给Sophus_INCLUDE_DIRS
find_package(Sophus REQUIRED)
include_directories(${Sophus_INCLUDE_DIRS})
#Pangolin生成一个libPangolin动态链接库
find_package(Pangolin REQUIRED)
include_directories(${Pangolin_INCLUDE_DIRS})

include_directories("/usr/include/eigen3")
#编译
add_executable(plotError compare_tra.cpp)
#链接
#target_link_libraries(plotError Sophus::Sophus)
target_link_libraries(plotError ${Sophus_LIBRARIES} )

target_link_libraries(plotError ${Pangolin_LIBRARIES})

compare_tra.cpp对应代码：

#include "sophus/so3.h"
#include "sophus/se3.h"
#include 
#include 
#include 
#include 
#include 
#include 
// need pangolin for plotting trajectory
#include 
using namespace std;
// path to trajectory file
string gt_file = "../groundtruth.txt";
string est_file = "../estimated.txt";
vector<Sophus::SE3, Eigen::aligned_allocator<Sophus::SE3>> gt_poses,est_poses;
// function for plotting trajectory, don't edit this code
// start point is red and end point is blue
void DrawTrajectory(vector<Sophus::SE3, Eigen::aligned_allocator<Sophus::SE3>> gt_poses,
                    vector<Sophus::SE3, Eigen::aligned_allocator<Sophus::SE3>> est_poses);
void readData(string filepath);
void ErrorTrajectory();
int main(int argc, char **argv) {
    readData(gt_file);
    readData(est_file);
    ErrorTrajectory();
    // draw trajectory in pangolin
    DrawTrajectory(gt_poses,est_poses);//打印两条轨迹
    return 0;
    /// implement pose reading code
    // start your code here (5~10 lines)
}
/*******************************************************************************************/
void readData(string filepath){
    vector<Sophus::SE3, Eigen::aligned_allocator<Sophus::SE3>> poses;
    ifstream infile(filepath);
    double t1,tx,ty,tz,qx,qy,qz,qw;
    string line;
    if(infile)
    {
        while(getline(infile,line))
        {
            stringstream record(line);    //从string读取数据
            record>>t1>>tx>>ty>>tz>>qx>>qy>>qz>>qw;
            Eigen::Vector3d t(tx,ty,tz);
            Eigen::Quaterniond q = Eigen::Quaterniond(qw,qx,qy,qz).normalized();  //四元数的顺序要注意
            Sophus::SE3 SE3_qt(q,t);
            poses.push_back(SE3_qt);
        }
    }
    else
    {
        cout<<"没找到这个文件"<<endl;
    }
    if(filepath==gt_file){
        gt_poses = poses;
    }else if( filepath==est_file ){
        est_poses = poses;
    }else{ cout<<"读文件出错"<<endl;}
    infile.close();
}
/*******************************************************************************************/
void ErrorTrajectory()
{
    double RMSE = 0;
    Eigen::Matrix<double ,6,1> se3;
    vector<double> error;
    for(int i=0;i<gt_poses.size();i++){
        se3=(gt_poses[i].inverse()*est_poses[i]).log();  //这里的se3为向量形式，求log之后是向量形式
        //cout<
        error.push_back( se3.squaredNorm() );  //二范数
        // cout<
    }
    for(int i=0; i<gt_poses.size();i++){
        RMSE += error[i];
    }
    RMSE /= double(error.size());
    RMSE = sqrt(RMSE);
    cout<<RMSE<<endl;
}
/*******************************************************************************************/
void DrawTrajectory(vector<Sophus::SE3, Eigen::aligned_allocator<Sophus::SE3>> gt_poses,
                    vector<Sophus::SE3, Eigen::aligned_allocator<Sophus::SE3>> est_poses) {
    if (gt_poses.empty()) {
        cerr << "groundtruth is empty!" << endl;
        return;
    }
    if (est_poses.empty()) {
        cerr << "estimated is empty!" << endl;
        return;
    }
    // create pangolin window and plot the trajectory
    pangolin::CreateWindowAndBind("Trajectory Viewer", 1024, 768);
    glEnable(GL_DEPTH_TEST);
    glEnable(GL_BLEND);
    glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);
    pangolin::OpenGlRenderState s_cam(
            pangolin::ProjectionMatrix(1024, 768, 500, 500, 512, 389, 0.1, 1000),
            pangolin::ModelViewLookAt(0, -0.1, -1.8, 0, 0, 0, 0.0, -1.0, 0.0)
    );
    pangolin::View &d_cam = pangolin::CreateDisplay()
            .SetBounds(0.0, 1.0, pangolin::Attach::Pix(175), 1.0, -1024.0f / 768.0f)
            .SetHandler(new pangolin::Handler3D(s_cam));
    while (pangolin::ShouldQuit() == false) {
        glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
        d_cam.Activate(s_cam);
        glClearColor(1.0f, 1.0f, 1.0f, 1.0f);//窗口,rgba
        glLineWidth(2);
        for (size_t i = 0; i < est_poses.size() - 1; i++) {
            glColor3f(1 - (float) i / est_poses.size(), 0.0f, (float) i / est_poses.size());
            glBegin(GL_LINES);
            auto p1 = est_poses[i], p2 = est_poses[i + 1];
            glVertex3d(p1.translation()[0], p1.translation()[1], p1.translation()[2]);
            glVertex3d(p2.translation()[0], p2.translation()[1], p2.translation()[2]);
            glEnd();
        }
        for (size_t i = 0; i < gt_poses.size() - 2; i++) {
            glColor3f(0.f, 0.8f, 0.f);//绿色
            glBegin(GL_LINES);
            auto p3 = gt_poses[i], p4 = gt_poses[i + 1];//只显示tx,ty,tz
            glVertex3d(p3.translation()[0], p3.translation()[1], p3.translation()[2]);
            glVertex3d(p4.translation()[0], p4.translation()[1], p4.translation()[2]);
            glEnd();
        }
        pangolin::FinishFrame();
        usleep(5000);   // sleep 5 ms
    }
}

然后运行，运行命令如下：

cd track_compare
cd build
cmake ..
make
./plotError

本人自学SLAM，如果错误，还请见谅留言提醒
希望的我的博客对你有帮助！