数据结构：树的基础知识

        本系列博客整理自网络，其中加入部分个人见解，如果你在看到这个系列的博客的时候有似曾相识的感觉，非常正常，主要是用于本人以后学习与复习，参考的原博客的地址我也会在博客前面或后面给出。

      数据结构中有很多树的结构，其中包括二叉树、二叉搜索树、2-3树、红黑树、B树、B+树、B*树等等下面从最基础的概念开始，介绍结构与实现。

1、什么是树？

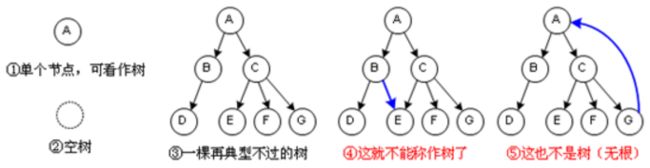
树是一种数据结构，可以用来表示层次关系，因表示的样子很像一颗倒立的树而得名。
在数据结构中的特点是一对多（链表是一对一，图是多对多）。

 

我们将最上面的结点叫做树根，也叫根节点；最下面的叫做树叶，也叫做叶子结点。

节点的度：一个结点拥有的子结点的个数即为该结点的度，如图3中C结点，有E、F、G三个子结点，那么C结点的度就是3。

叶子结点（终端结点）：没有子结点的结点，比如图3中的D、E、F、G。

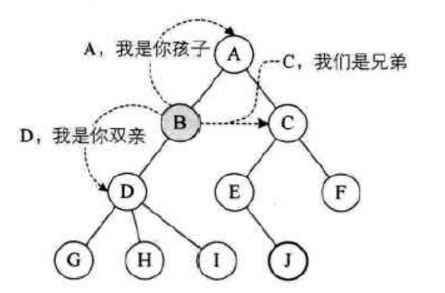
孩子结点：某一个结点的子结点成为孩子结点。比如图3中B、C就是A的孩子结点。

双亲结点：与孩子结点相反。比如图3中，A就是B、C的双亲结点。

兄弟结点：同一个双亲结点的孩子结点，相互之间成为兄弟结点。比如图3中的B、C。

树的高度：其实就是该树的层数，这棵树有几层，就有多高；对于某个结点，那么就是该结点所在的层数了。所以高度是从下往上数。如图3，A的高度就是3，B、C为2。

树的深度：从根结点开始往下数，根结点为1。所以对于某个结点，它的深度和高度可能不是一样的。如图3，树的深度就是3，B、C的深度为2。

树的宽度：具有最多结点数的层中包含的结点数。一般都是用于二叉树。

2、树的存储结构

     下面所有的分析都是基于上面这张图

双亲表示法

       双亲的含义我们上面讲述过了。我们假设以一组连续空间存储树的结点，同时在每个结点中，附设一个指示器指向其双亲结点到链表中的位置。也就是说每个结点除了知道自己之外还需要知道它的双亲在哪里。下图中data代表各个节点，parent代表该节点对应双亲的下表地址。

这种结构对于查找双亲很方便，但是对于查找孩子节点就比较麻烦，需要遍历全树。

以下是我们的双亲表示法的结构定义代码：

/*树的双亲表示法结点结构定义  */  
#define MAXSIZE 100  
typedef int ElemType;        //树结点的数据类型，暂定为整形   
typedef struct PTNode        //结点结构  
{  
    ElemType data;          //结点数据  
    int parent;              //双亲位置  
}PTNode;  
  
typedef struct 
{  
    PTNode nodes[MAXSIZE];  //结点数组  
    int r,n;                 //根的位置和结点数  
}PTree;

孩子表示法

把每个结点的孩子排列起来，以单链表做存储结构，则n个结点有n个孩子链表，如果是叶子结点则此单链表为空。然后n个头指针有组成一个线性表，采用顺序存储结构，存放进入一个一维数组中。孩子表示法，与双亲表示法恰恰相反，双亲节点记录自己的孩子节点，获取最大的数的度，本图中数的最大度为3，所以如图所示：

以下是孩子表示法的结构定义代码：

/*树的孩子表示法结点结构定义  */  
#define MAXSIZE 100  
typedef int ElemType;         //树结点的数据类型，暂定为整形   
typedef struct CTNode        //孩子结点  
{  
    int child;  
    struct CTNode *next;  
}*ChildPtr;  
  
typedef struct               //表头结构  
{  
    ElemType data;  
    ChildPtr firstchild;  
}CTBox;  
typedef struct               //树结构  
{  
    CTBox nodes[MAXSIZE];   //结点数组  
    int r,n;                 //根结点的位置和结点数  
}CTree;  

孩子兄弟表示法

如图所示，双亲节点记录了，第一个孩子几点，第一个孩子节点记录他的孩子几点及兄弟节点。

3、二叉树

什么是二叉树？

二叉树的每个结点至多只有二棵子树(不存在度大于2的结点)，二叉树的子树有左右之分，次序不能颠倒。

#代表为空

二叉树的性质:

1、二叉树不存在度大于2的结点。
2、左右子树是有顺序的，即使某结点只有一棵子树，也要区分它是左子树还是右子树。
3、根据(2)所说，二叉树具有五种基本形态：空二叉树、只有一个根节点、只有左子树、只有右子树、左右子树都有。
4、二叉树第i层上至多有2^(i-1)个结点(i≥1)。
5、深度为k的二叉树至多有2^k - 1个结点(k≥1)，此时为满二叉树。
6、对任何一棵二叉树T，如果其叶子结点数为n0，度为2的结点数为n2，则n0 = n2 + 1。这个的推导：设结点数为n，可以知道结点间连接线数为n-1。于是有两个式子：n-1 = n1 + 2*n2 和 n = n0 + n1 +n2，联合解出n0 = n2 + 1

7、具有n个结点的完全二叉树的深度为log2 n向下取整然后加1 => 通过满二叉树2^n - 1可以推出。

8、对于完全二叉树，在有左右子结点的情况下，设根结点的编号是n(这个编号从1开始)，则左孩子的编号是2n，右孩子的编号是2n+1。

满二叉树和完全二叉树：

满二叉树：除最后一层无任何子节点外，每一层上的所有结点都有两个子结点。也可以这样理解，除叶子结点外的所有结点均有两个子结点。节点数达到最大值，所有叶子结点必须在同一层上。

完全二叉树：若设二叉树的深度为h，除第 h 层外，其它各层 (1～(h-1)层) 的结点数都达到最大个数，第h层所有的结点都连续集中在最左边，这就是完全二叉树。

注：完全二叉树是效率很高的数据结构，堆是一种完全二叉树或者近似完全二叉树，所以效率极高，像十分常用的排序算法、Dijkstra算法、Prim算法等都要用堆才能优化，二叉排序树的效率也要借助平衡性来提高，而平衡性基于完全二叉树。

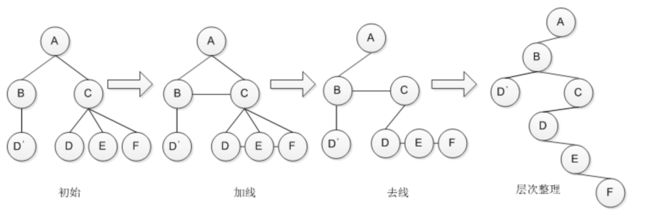
如何将非二叉树转化为二叉树？

（1）将该树的所有兄弟连在一起。

（2）除了保留每个结点它的左孩子结点，将于其连接的其他孩子全部断开。

（3）最后展开，就得到了二叉树。

具体图示见下图。

二叉树的遍历

二叉树的遍历分为先序（前序）、中序、后序和层次遍历，下面分别介绍这个遍历的方法。

 

/* 先序遍历(非递归) 
   思路：访问T->data后，将T入栈，遍历左子树；遍历完左子树返回时，栈顶元素应为T，出栈，再先序遍历T的右子树。 
*/  
void PreOrder2(BiTree T){  
    stack stack;  
    //p是遍历指针  
    BiTree p = T;  
    //栈不空或者p不空时循环  
    while(p || !stack.empty()){  
        if(p != NULL){  
            //存入栈中  
            stack.push(p);  
            //访问根节点  
            printf("%c ",p->data);  
            //遍历左子树  
            p = p->lchild;  
        }  
        else{  
            //退栈  
            p = stack.top();  
            stack.pop();  
            //访问右子树  
            p = p->rchild;  
        }  
    }//while  
}  

【思路】：T是要遍历树的根指针，中序遍历要求在遍历完左子树后，访问根，再遍历右子树。

 先将T入栈，遍历左子树；遍历完左子树返回时，栈顶元素应为T，出栈，访问T->data，再中序遍历T的右子树。

void InOrder2(BiTree T){  
    stack stack;  
    //p是遍历指针  
    BiTree p = T;  
    //栈不空或者p不空时循环  
    while(p || !stack.empty()){  
        if(p != NULL){  
            //存入栈中  
            stack.push(p);  
            //遍历左子树  
            p = p->lchild;  
        }  
        else{  
            //退栈，访问根节点  
            p = stack.top();  
            printf("%c ",p->data);  
            stack.pop();  
            //访问右子树  
            p = p->rchild;  
        }  
    }//while  
}  

【思路】：T是要遍历树的根指针，后序遍历要求在遍历完左右子树后，再访问根。需要判断根结点的左右子树是否均遍历过。

//后序遍历(非递归)  
typedef struct BiTNodePost{  
    BiTree biTree;  
    char tag;  
}BiTNodePost,*BiTreePost;  
  
void PostOrder2(BiTree T){  
    stack stack;  
    //p是遍历指针  
    BiTree p = T;  
    BiTreePost BT;  
    //栈不空或者p不空时循环  
    while(p != NULL || !stack.empty()){  
        //遍历左子树  
        while(p != NULL){  
            BT = (BiTreePost)malloc(sizeof(BiTNodePost));  
            BT->biTree = p;  
            //访问过左子树  
            BT->tag = 'L';  
            stack.push(BT);  
            p = p->lchild;  
        }  
        //左右子树访问完毕访问根节点  
        while(!stack.empty() && (stack.top())->tag == 'R'){  
            BT = stack.top();  
            //退栈  
            stack.pop();  
            BT->biTree;  
            printf("%c ",BT->biTree->data);  
        }  
        //遍历右子树  
        if(!stack.empty()){  
            BT = stack.top();  
            //访问过右子树  
            BT->tag = 'R';  
            p = BT->biTree;  
            p = p->rchild;  
        }  
    }//while  
}  

<4>层次遍历

【思路】：按从顶向下，从左至右的顺序来逐层访问每个节点，层次遍历的过程中需要用队列。

//层次遍历  
void LevelOrder(BiTree T){  
    BiTree p = T;  
    //队列  
    queue queue;  
    //根节点入队  
    queue.push(p);  
    //队列不空循环  
    while(!queue.empty()){  
        //对头元素出队  
        p = queue.front();  
        //访问p指向的结点  
        printf("%c ",p->data);  
        //退出队列  
        queue.pop();  
        //左子树不空，将左子树入队  
        if(p->lchild != NULL){  
            queue.push(p->lchild);  
        }  
        //右子树不空，将右子树入队  
        if(p->rchild != NULL){  
            queue.push(p->rchild);  
        }  
    }  
}  

参考博客：

http://blog.csdn.net/gaopeng0071/article/details/24913951

http://blog.jobbole.com/111680/

http://blog.csdn.net/htyurencaotang/article/details/12406223

http://blog.csdn.net/x1247600186/article/details/24670775

http://www.cnblogs.com/tyrus/archive/2016/09/08/ds_tree.html

http://blog.chinaunix.net/xmlrpc.php?r=blog/article&uid=27570663&id=4432842

http://www.cnblogs.com/skywang12345/p/3576328.html