数据结构与算法之堆排序

1、先修知识点

        看懂本篇文章的前提是要对树这种数据结构有所了解，堆排序其实是树结构的一个应用，和冒泡排序、选择排序、插入排序、希尔排序、归并排序、快速排序类似，它也是一种排序方法。

        要想继续往下学习，先去学习树和完全二叉树的基本概念、判断方法和存储方式。或者你私信我，我发简单知识点的视频给你，不然就去网上找一找。

2、大顶堆和小顶堆的理论介绍

• 堆排序是利用堆这种数据结构（其实就是树结构）而设计的一种排序算法，堆排序是一种树形选择排序，不使用遍历的方式查找待排序区间最大数,而是通过堆来选择待排序区间最大数，它也是不稳定排序。（PS：或许这样说有些抽象，等我后面讲解完，你再来看这些理论的东西！）
• 堆是具有以下性质的完全二叉树：每个结点的值都大于或者等于其左右孩子结点的值，称为大顶堆，注意：没有要求结点的左孩子的值和右孩子的值的大小关系。
• 每个结点的值都小于或者等于其左右孩子结点的值，称为小顶堆。

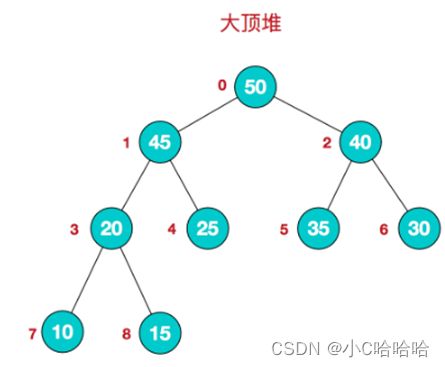
举一个大顶堆的例子，如下图： 首先是一棵完全二叉树，且每个结点的值都大于等于左右孩子结点的值。

对于以上的大顶堆而言，如果使用顺序存储，那我们可以这样存：对堆中的结点进行编号，映射到数组中，观察数组有如下特点：arr[i] >= arr[2*i+1] 且 arr[i] >= arr[2*i+2]，其中i代表结点的编号，编号从0开始。

 

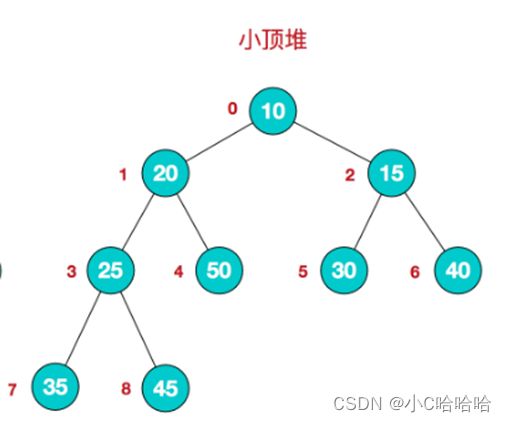
 再举一个小顶堆的例子，如下图： 首先是一棵完全二叉树，且每个结点的值都小于等于左右孩子结点的值。和大顶堆类似，小顶堆需要满足条件：arr[i]<=arr[2*i+1] 且 arr[i] <= arr[2*i+2]，其中i代表结点的编号，编号从0开始。

 说明：如果使用堆排序，一般是通过构建大顶堆来完成升序排列，构建小顶堆来完成降序排列。

3、堆排序的基本思想

1、将待排序序列构造成一个大顶堆（大顶堆用数组来存储）

2、此时，整个序列的最大值就是堆顶的根节点。

3、将其与末尾元素进行交换，此时末尾就为最大值。

4、然后将剩余的n-1个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列了。

4、堆排序的案例演示

看完以上的4个步骤，或者你还是一脸茫然，别说你了，我也是，我们来举一个具体的案例来看一下。

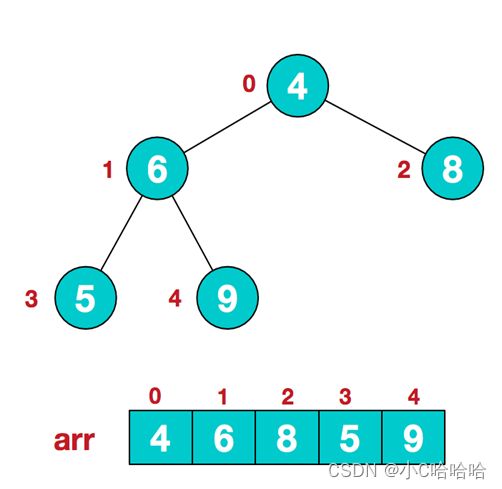
要求：给你一个数组{4,6,8,5,9}，要求使用堆排序，将数组升序排列。

 第一大步：构造初始堆。将给定的无序序列{4,6,8,5,9}构造成一个大顶堆（因为是升序排列，所以这里可以构造大顶堆）

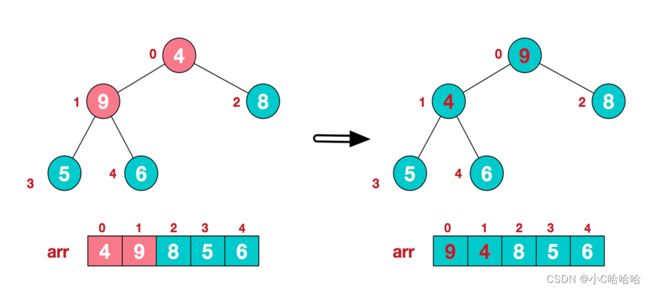
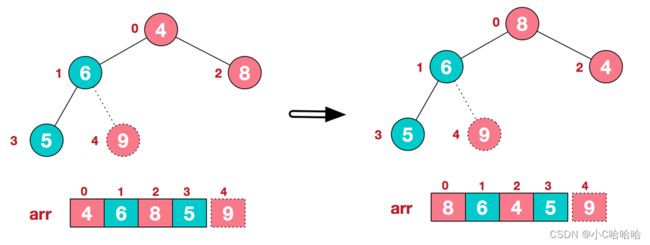
 1、此时我们从最后一个非叶子结点开始（叶结点不用调整，第一个非叶子结点：长度/2-1，以此图为例，就是5/2-1=1号节点，此结点为第一个非叶子结点），通过观察，发现第一个非叶子结点的值，比右子结点的值还小，于是将6和9进行交换，得到如右所示的图。

经过第一次调整，局部大顶堆就构建完成了，紧接着继续构建。

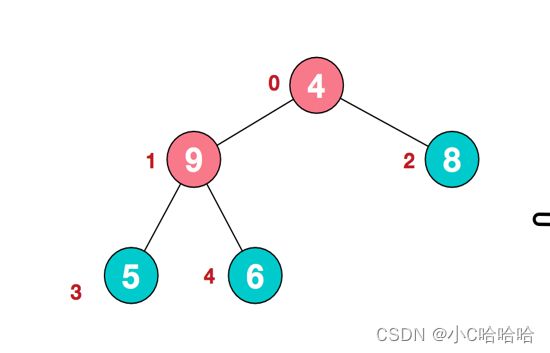
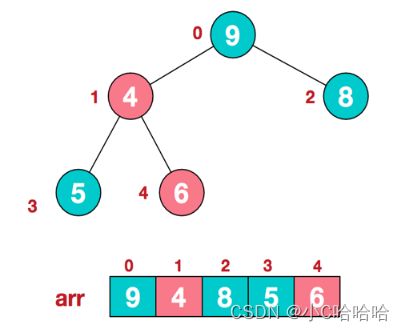
2、找到第二个非叶子结点4，由于[4,9,8]中9元素最大，4和9交换，如下图所示：

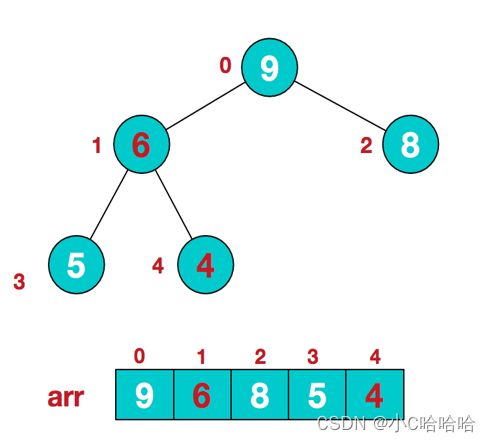
注意，这时观察，整个二叉树，此时它还不是一个大顶堆，因为本次交换导致了[4,5,6]结构混乱，因此继续调整。[4,5,6]中6最大，交换4和6，如下图所示：

此时，我们就将一个无序序列构造成了一个大顶堆。

第二大步：将堆顶元素与末尾元素进行交换，使末尾元素最大。然后继续调整堆，再将堆顶元素与末尾元素交换，得到第二大元素。如此反复进行交换，重建，交换。

1、将堆顶元素9和末尾元素4进行交换

 

 2、重新调整树结构，使其继续满足大顶堆的定义

 3、再将堆顶元素8与末尾元素5进行交换，得到第二大元素8

 

4、后续过程，继续进行调整、交换，如此反复进行，最终使得整个序列有序

 以上就完成了序列的升序排列，先从宏观上理解一下堆排序大概的一个过程是怎样的，当然，其中还有很多细节，在代码中才能体现得更加清楚。

 4、堆排序的代码实现

堆排序的代码确实比较难理解，我们需要把每一句代码的含义都搞清楚，我不妨以上面这个序列{4,6,8,5,9} 为例来编写代码。

其实堆排序最关键的核心步骤就是：如何进行大根堆调整？先看代码吧！然后按照我的分析一步一步理解

// 将一个数组（二叉树）调整成一个大顶堆 
// 举例：int arr[] = {4,6,8,5,9}; => i=1 => adjustHeap => 得到{4,9,8,5,6}
// 如果我们再次调用adjustHeap 传入的是i=0 => 得到 {9,6,8,5,4} 
// arr表示待调整的数组， 
// i表示非叶子结点的在数组中的索引 
// length表示对多少个元素进行调整，length 表示在逐渐减少 
// 完成将以i对应的叶子结点的树调整大顶堆 
void adjustHeap(int arr[],int i,int length) {
	int temp = arr[i];  //先取出当前元素的值保存在一个临时变量temp中
	//开始调整
	for(int k=2*i+1;ktemp) {
			arr[i] = arr[k];  //把较大的值赋给当前i结点
			i = k; //让i指向k，继续循环比较  
		}
		else {
			break; 
		} 
	} 
	//当for循环结束后，已经将以i为父结点的树的最大值放在了最顶上 
	arr[i] = temp;  //将temp赋值放到调整后的位置 
}

思路：首先告诉要调整的数据—数组arr，以上述序列为例，然后找到要调整的结点i，i代表结点的编号，最后要知道对多少个元素length进行调整，在初始化情况下，数组的长度length为5，首先根据i=(len/2-1)公式得到i=1，于是对1号结点进行调整。怎么调整呢？

① 取出当前i=1号元素6保存到临时变量temp中，然后找到i=1号结点的左孩子结点编号3将其赋值给k变量，即k=3，然后与编号为k+1=4的右孩子结点进行比较，如果发现左孩子结点的值大于右孩子结点的值，就先将k的值自增1，在这里我们发现arr[3]=5 > arr[4]=9，于是将k的值自增1，k变为4，即k=4。

② 如果发现arr[k]的值大于temp，说明需要进行调整，执行arr[i]=arr[k]语句，并且执行i=k语句，否则的话，直接退出for循环；以本例子为例，发现arr[4]等于9大于temp6，于是执行arr[1]=arr[4]的操作，此时将9赋值给arr[1]，还需要将k=4这个值赋值给i，此时i=4，代表即将以4为根结点，准备继续大顶堆的调整，但是，在for循环的时候发现k=2*4+1=9，不满足小于length的条件，退出for循环

③ 当for循环结束后，将temp赋值给arr[i]，此时所有的arr[i]都会大于等于左右孩子的值。

经过以上三步，以[9,5,6]为元素的大顶堆就调整好了，接下来我们继续举例子来理解。

以上的代码需要多琢磨，多研究，不然一时半会真的很难读懂。

接下来继续进行调整，找到第2个非叶子结点4，如下图所示：

 

 按照刚刚的步骤继续进行调整（你可以对照着代码理解）

① 取出当前i=0号元素4保存到临时变量temp中，然后找到i=0号结点的左孩子结点编号1将其赋值给k变量，即k=1，然后与编号为k+1=2的右孩子结点进行比较，如果发现左孩子结点的值大于右孩子结点的值，就先将k的值自增1，在这里我们发现arr[1]并没有大于arr[2]，所以k的值还是保持原来的1不变。注意，元素4已经保存在temp变量中了。

 

② 如果发现arr[k]的值大于temp，即大于arr[i]，那就需要进行调整，执行arr[i]=arr[k]语句，即arr[0]=arr[1]语句，即arr[0]=9，此时继续让k赋值给i，即i=k，那么此时i=1，注意，temp中依然存储的是4这个数。

 

③ 因为i=0的结点调整后有可能会影响之前已经调整好的大顶堆，因此继续执行for循环，重新将k赋值为k=2*k+1，继续调整以k为根结点的树，即k=3，，然后比较arr[3]和arr[4]的值，发现arr[3]>arr[4]，于是让k自增1，k变为4。发现arr[4]==6 >temp==4，于是将6赋值给arr[1]，此时将k=4赋值给i，i此时为4。继续执行for循环，发现条件不满足，退出for循环，此时需要将原来temp的值赋值给arr[i]，即arr[4]=4。

 以上是整个堆排序当中的核心代码 — 调整堆。

我们再来回顾一下堆排序的整体步骤：

1).将无序序列构建成一个堆，根据升序降序需求选择大顶堆或小顶堆;

2).将堆顶元素与末尾元素交换，将最大元素"沉"到数组末端;

3).重新调整结构，使其满足堆定义，然后继续交换堆顶元素与当前末尾元素，反复执行调整+交换步骤，直到整个序列有序。

从主函数出发，我们可以这样来编写代码：

int main() {
	//要求将数组进行升序排列 
	int arr[] = {4,6,8,5,9}; 
	heapSort(arr,5);
	return 0;
}

 其中，heapSort代表要用堆排序的方法堆arr数组进行升序排列，5代表数组元素的长度。

然后，再来看一下heapSort的具体代码细节

//编写一个堆排序的方法，
void heapSort(int arr[],int len) {
    //1.初始堆，先把无序序列调成一个大顶堆
	for(int i=len/2-1;i>=0;i--) {
		adjustHeap(arr,i,5);
	} 
	
	//2.将堆顶元素与末尾元素交换，将最大元素"沉"到数组末端
	for(int j=5-1;j>0;j--) {
		//交换
		int temp = arr[j];
		arr[j] = arr[0];
		arr[0] = temp; 
		adjustHeap(arr,0,j);    
	} 
	
	for(int i=0;i<5;i++) cout << arr[i] << "  ";
	cout << endl;	
} 

首先，先把无序序列进行初始化，调整成一个大顶堆，然后进行堆顶元素和末尾元素的交换，每次交换完毕之后需要对堆重新进行调整，这里，我只有5个元素，因此，需要交换4次。

 5、堆排序的完整代码实现

#include 
using namespace std;

// 将一个数组（二叉树）调整成一个大顶堆 
// 举例：int arr[] = {4,6,8,5,9}; => i=1 => adjustHeap => 得到{4,9,8,5,6}
// 如果我们再次调用adjustHeap 传入的是i=0 => 得到 {9,6,8,5,4} 
// arr表示待调整的数组， 
// i表示非叶子结点的在数组中的索引 
// length表示对多少个元素进行调整，length 表示在逐渐减少 
// 完成将以i对应的叶子结点的树调整大顶堆 
void adjustHeap(int arr[],int i,int length) {
	int temp = arr[i];  //先取出当前元素的值保存在一个临时变量temp中
	//开始调整
	for(int k=2*i+1;ktemp) {
			arr[i] = arr[k];  //把较大的值赋给当前i结点
			i = k; //让i指向k，继续循环比较  
		}
		else {
			break; 
		} 
	} 
	//当for循环结束后，已经将以i为父结点的树的最大值放在了最顶上 
	arr[i] = temp;  //将temp赋值放到调整后的位置 
}
//编写一个堆排序的方法，
void heapSort(int arr[],int len) {
	cout << "堆排序" << endl;
	//分步完成
	/*
	adjustHeap(arr,1,len);
	for(int i=0;i<5;i++) cout << arr[i] << "  ";
	cout << endl;
	
	adjustHeap(arr,0,len);
	for(int i=0;i<5;i++) cout << arr[i] << "  ";
	cout << endl;
	*/
	//将无序序列构建一个堆，根据升序降序需求选择大顶堆或者小顶堆
	for(int i=len/2-1;i>=0;i--) {
		adjustHeap(arr,i,5);
	} 
	
	//2.将堆顶元素与末尾元素交换，将最大元素"沉"到数组末端
	for(int j=5-1;j>0;j--) {
		//交换
		int temp = arr[j];
		arr[j] = arr[0];
		arr[0] = temp; 
		adjustHeap(arr,0,j);    //adjustHeap(arr,0,3) 
	} 
	
	
	for(int i=0;i<5;i++) cout << arr[i] << "  ";
	cout << endl;	
} 
int main() {
	//要求将数组进行升序排列 
	int arr[] = {4,6,8,5,9}; 
	heapSort(arr,5);
	return 0;
}