csapp:cachelab实验-PartB-2
热乎的缓存实验,昨天刚结束的计算机系统实验,最后前几天不是在玩手机丧志,就是赶bomb实验,做两门课的讨论课ppt。最后星期六晚终于把bomb实验的前五关给过了,最后一关还没通过,然后星期天还有算法设计的雨课堂作业和cachelab实验的最后一部分PartB,优化64x64和67x61矩阵转置。当天晚上先给过了四个雨课堂的题目,最后还剩6道,还是决定做cache实验。----2020.5-11HNU某菜学子
实验目标:使用C语言来模拟CPU对cache的访问,然后统计hits、misses和evictions。更好的理解高速缓存对于C语言程序性能的影响。
资源:linux-64位ubuntu18.04环境下,virtual box虚拟机软件,valgrind-3.12.跟踪trace文本,Linux下检测内存泄漏工具,python用于测试最终结果,cachelab-handout文件
实验步骤:首先在linux环境终端用命令“linux> tar xvf cachelab-handout.tar”将文件降压,否则有可能会被影响;阅读cachelan.pdf了解相关知识,任务,要求。安装valgrind软件,就可以开始PartA的设计了。根据cache跟踪模拟器,来模拟一个cache,写出代码csim.c。开始编译调试,命令“make”来生成各类文件,”make clean”清除“make”命令生成的文件。用命令“./csim-ref [-hv] -s-E -b -t ”查看跟踪情况,学习cache的miss,hit知识。
命令“./csim -s 4 -E 2 -b 4 -t traces/yi.trace”检查第一个跟踪结果,命令“./driver.py”查看PartA是否完全正确。正确之后开始做PartB,实现矩阵的转置。编写补充trans.c,设置转置函数。命令make,“./test-trans -M 64 -N 64”生成对应矩阵的.traces跟踪文件,“./csim -v -s 5 -E 1 -b 5 -t trace.f1”来查看跟踪结果,详细miss情况。最后设计trans成功后,用./driver.py查看最终得分。
**啰啰嗦嗦得到组索引和标志位的部分**
本来以为这部分很简单的,但是经过我一系列的磨蹭,还是ddl了,在找出64x64的组索引和标志位分部上,搞了好长时间,对于我这颗不太灵光的脑袋来说,果然还是太难了,把tag和set打印出来一个个数吧,数着数着就忘了数到哪了,怎么说也有个64x64行呢,或者就是数着数着就不想数了,如此往复,耽误了太多时间。还想着./csim -v -s 5 -E 1 -b 5 -t ,traces文件是traces.f0呢还是traces.f1呢,又去观察了一下L指令的地址变化,确定了.f0是自己写的transpose函数生成的trace文本,.f1是不分块访问的trace脚本。然后就跟踪traces.f1看set和tag的分块了,得到了以下结果

接下来就根据set和tag分块来优化了
分块编写N64和N67转置
- M64N64优化
评分标准:miss>2000 0分 miss<1300 满分8分
![]()
1)进行8分块,并且继续进行4分块的代码如像下图。和命中情况

![]()
miss=1891 结果只能勉强不打个0分,得继续优化
2)在1)基础上优化对角线后(也就是L,S指令分别进行,这样能减少访问A,B数组带来的冲突),效果不大
int x1,x2,x3,x4,x5,x6,x7,x8;//在我经历ddl几分钟,因为网上代码都是图片并且格式不对没成功写完后,我就决定我要做个好人,直接把代码部分贴出来
int block=8,i,j,ii,jj;
for(i=0;i<M;i+=block)
for(j=0;j<N;j+=block)
for(ii=i;ii<i+block;ii++)
{
if(i==j){
x1=A[ii][j];x2=A[ii][j+1];x3=A[ii][j+2];x4=A[ii][j+3];
x5=A[ii][j+4];x6=A[ii][j+5];x7=A[ii][j+6];x8=A[ii][j+7];
B[j][ii]=x1;B[j+1][ii]=x2;B[j+2][ii]=x3;B[j+3][ii]=x4;
B[j+4][ii]=x5;B[j+5][ii]=x6;B[j+6][ii]=x7;B[j+7][ii]=x8;
continue;
}
for(jj=j;jj<j+block;jj++)
{
B[jj][ii]=A[ii][jj];
}
}
![]()
向满分又近了一步,但还不够
3)在进行分块基本上循环展开的效果,同样也不大(下图),未达到满分要求
其实所谓的循环展开和前面的第2)不一样就是直接展开,不加个if(j==i)而已
![]()
又前进了一小步
4) 在分块2)的基础上,交换一下4x4小块的写入顺序,即数组B的访问。代码部分在1)的基础上把最后两行删掉,加上一下代码段
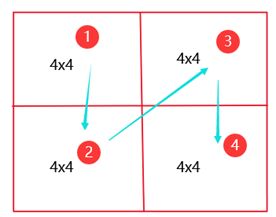
优化过程:根据2)先8分块,在4小分块,对于A数组来说,先是访问左上的4x4矩阵(1号),接着是右上角4x4矩阵(2号),左下角(3号)、右下角4x4矩阵(4号)。而数组B的访问理应是1,3,2,4的顺序,
但是考虑到标志位和组索引产生的miss,可以在访问1,2时正常的访问进行转置,而访问3的时候,A数组访问完,B数组先不急着访问,先把这16个元素存到临时变量,在访问4号4x4矩阵的时候再,将16个临时变量存到B数组中,4号小矩阵也正常访问,转置到B数组。miss=1203,比2)miss数减少了将近600,效果不错。
int i,j,ii,jj,block;
if(N==64&&M==64)
{
int i3;
int p=-1;
int x1,x2,x3,x4,y1,y2,y3,y4,y5,y6,y7,y8,y9,y10,y11,y12,y13,y14,y15,y16;
block=8;
for(i=0;i<M;i+=block)
for(j=0;j<N;j+=block)//8分块
for(ii=i;ii<8+i;ii+=4)
for(jj=j;jj<8+j;jj+=4)//4小分块
for(i3=ii;i3<ii+4;i3++)
{
if(jj!=j&&p==-1)//2号4x4小矩阵,先存起来
{
y1=A[ii][jj];y2=A[ii][jj+1];y3=A[ii][jj+2];y4=A[ii][jj+3];
y5=A[ii+1][jj];y6=A[ii+1][jj+1];y7=A[ii+1][jj+2];y8=A[ii+1][jj+3];
y9=A[ii+2][jj];y10=A[ii+2][jj+1];y11=A[ii+2][jj+2];y12=A[ii+2][jj+3];
y13=A[ii+3][jj];y14=A[ii+3][jj+1];y15=A[ii+3][jj+2];y16=A[ii+3][jj+3];
p=1;//表示有一个4x4的矩阵记录在临时变量
break;
}
else if(jj!=j&&p==1)//4号4x4小矩阵
{
B[jj][ii-4]=y1;B[jj][ii-3]=y5;B[jj][ii-2]=y9;B[jj][ii-1]=y13;//2号矩阵写入
B[jj+1][ii-4]=y2;B[jj+1][ii-3]=y6;B[jj+1][ii-2]=y10;B[jj+1][ii-1]=y14;
B[jj+2][ii-4]=y3;B[jj+2][ii-3]=y7;B[jj+2][ii-2]=y11;B[jj+2][ii-1]=y15;
B[jj+3][ii-4]=y4;B[jj+3][ii-3]=y8;B[jj+3][ii-2]=y12;B[jj+3][ii-1]=y16;
p=-1;//没有矩阵被记录
for(;i3<ii+4;i3++)//4号小矩阵可以直接转置
{
x1=A[i3][jj];x2=A[i3][jj+1];x3=A[i3][jj+2];x4=A[i3][jj+3];
//x5=A[ii][j+4];x6=A[ii][j+5];x7=A[ii][j+6];x8=A[ii][j+7];
B[jj][i3]=x1;B[jj+1][i3]=x2;B[jj+2][i3]=x3;B[jj+3][i3]=x4;
}
break;
}
//1、如果是1,3号4x4小矩阵,就直接转置
x1=A[i3][jj];x2=A[i3][jj+1];x3=A[i3][jj+2];x4=A[i3][jj+3];
//x5=A[ii][j+4];x6=A[ii][j+5];x7=A[ii][j+6];x8=A[ii][j+7];
B[jj][i3]=x1;B[jj+1][i3]=x2;B[jj+2][i3]=x3;B[jj+3][i3]=x4;
}
![]()
成功迈向满分miss=1203
- 追踪分析M64N64的组索引,分析8分块优化处理过程:
对于常规的8分块加四小分块优化:得到的结果miss数为1891,还不算很好的结果。对于B数组来说:它的访问顺序是可以用下图1表示,每个是个8x8矩阵,而在8小矩阵的访问顺序又如下图2表示。从④号的4x4小矩阵转到②号的小矩阵时,元素组索引不变,但是每一行的标志位都改变了,所以就会出现4个miss,同理②转③,③转④都会出现miss。再加上从当前8x8小矩阵向下转到另一个8x8的矩阵时,同样,组数分布未变,但是标志位已变,miss。所以相当于,每一个8x8矩阵访问时会有44=16次miss,而这样的转换每8列会出现7次,总共就有(3+46)48=864个miss左右


对于A数组,它的访问8x8内的访问顺序如上图(最右)所示。在②转③的时候也有B数组访问出现miss的情况那就大约有488=256,但是A数组的访问和B数组的访问经常是交叉出现的。也就是L,S,L,S…,就会出现一些前后L,S指令访问的cache块是同一块,但是两者的标志位是肯定不相同的,就会出现miss。
8分块有个致命的缺陷就是在上面描述B数组miss的原因,由于一行64个元素,导致标志位可以说是每四行换一个,同时组索引也是每四行一个,就导致一旦从上一个4x4小矩阵跳到下面的4x4小矩阵,就会出现miss,而且这里的访问B数组还是跳来跳去的。所以该方案不是最优的方案。所以就考虑将①②③④的B数组访问顺序交换,变成第1点所说的①③②④,这样一来,B数组分别访问①③和②④的时候,两个块的组索引相同,标志位也相同,就减少了miss数,只有从③跳到②才会有miss,每个8x8块都减少了这样的miss,整体也就减少了很多miss,效果不错。 - M61N67优化
没想到什么好方法,就只能分块了1、block=8
![]()
2、block=16,miss=1992,满分![]()
3、block=17,miss=1950,满分
![]()
else if(M==61&&N==67)
{
block=17;
for(i=0;i<N;i+=block)
for(j=0;j<M;j+=block)
for(ii=i;ii<N&&ii<i+block;ii++)
for(jj=j;jj<M&&jj<j+block;jj++)
B[jj][ii]=A[ii][jj];
还有其他.blck=18,miss=2021,block=4,时,miss=2425,block=12,时miss=2057…能找到的最优的就是分块17了,这个时候miss<2000,也算是满足要求了。根据这几个我们也可以看出block和miss并不会有什么规律的变化,而由于cache有空间局部性时间局部性,所以,miss数受多重因素影响。

在网上看到有人能找些一些其他方法,1、16分块基础上,进行循环展开,

