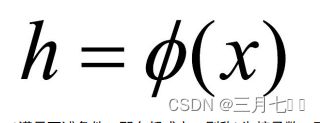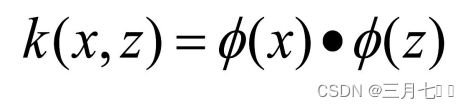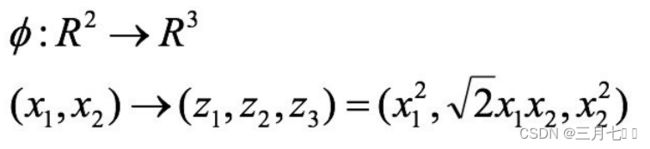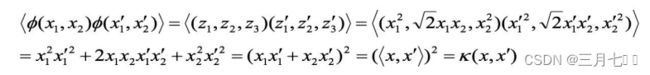机器学习---支持向量机的初步理解
1. SVM的经典解释
改编自支持向量机解释得很好 |字节大小生物学 (bytesizebio.net)
话说,在遥远的从前,有一只贪玩爱搞破坏的妖怪阿布劫持了善良美丽的女主小美,智勇双全
的男主大壮挺身而出,大壮跟随阿布来到了妖怪的住处,于是,妖怪将两种能量球吐到了桌子上,
并要求大壮用他手里的棍子将两种能量球分开,如果大壮能赢得游戏,就成全他和小美。
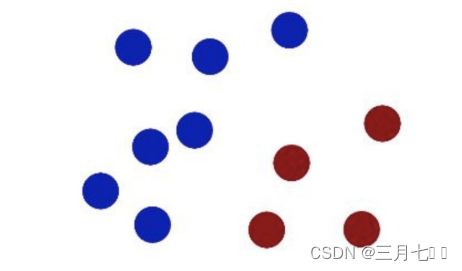
大壮思索了片刻,就将他手里的棍子放了上去,正好将两种能量球分到不同阵营。
然后阿布胸有成竹的又吐出了新的球,恰巧有一个球在不属于他的阵营。
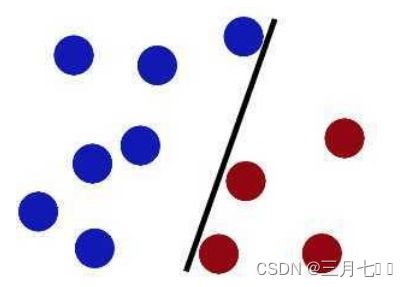
大壮将手里的棍子变粗,并试图通过在棍子两侧留出尽可能大的间隙来将棍子放在最佳位置。
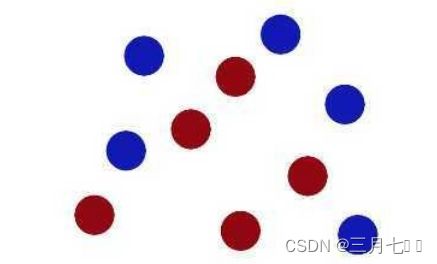
阿布气急败坏,将桌子上的能量球全部打乱顺序。
大壮一时间想不出办法,阿布转身就要和小美去玩游戏,大壮很生气的拍了一下桌子,恍然
大悟,并将手里的棍子扔了出去。
在阿布的眼中,棍子正好穿过了所有的能量球,并将其划分在不同的领域。
棍子也恰好打在了阿布的头上,大壮和小美幸福的生活在了一起。
经过后人的杜篡,将球写成了数据(data),将棍子写为了分类(classifier ),将最大间隙
写成了最优化(optimization)、将拍桌子描绘成核方法(kernelling),将桌子写为超平面
(hyperplane)。
2. SVM的算法定义
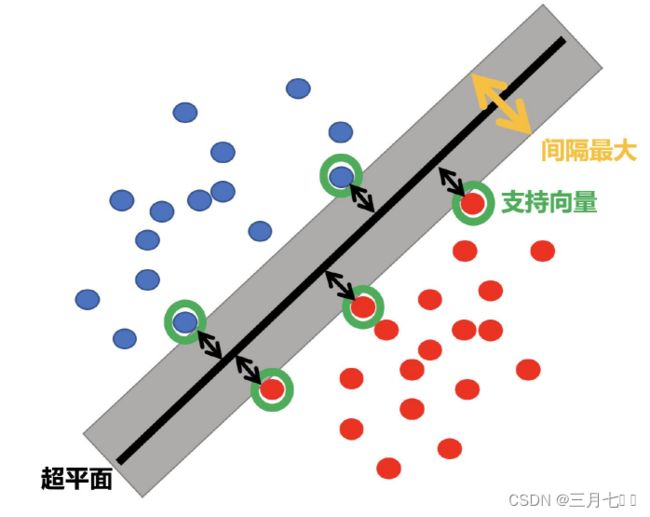
SVM全称是supported vector machine(⽀持向量机),即寻找到⼀个超平⾯使样本分成两
类,并且间隔最大。 SVM能够执⾏线性或非线性分类、回归,甚⾄是异常值检测任务。它是机器
学习领域最受欢迎的模型之⼀。SVM特别适用于中小型复杂数据集的分类。
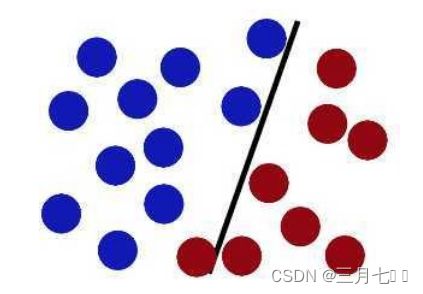
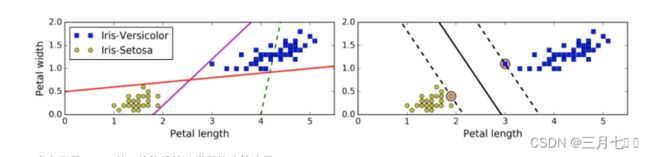
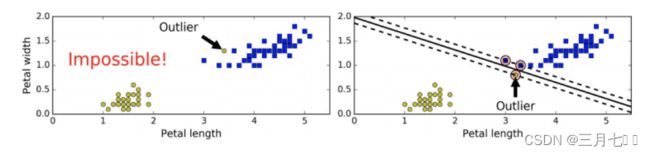
上左图显示了三种可能的线性分类器的决策边界:虚线所代表的模型表现非常糟糕,甚至都
⽆法正确实现分类。其余两个模型在这个训练集上表现堪称完美,但是它们的决策边界与实例过于
接近,导致在面对新实例时,表现可能不会太好。 右图中的实线代表SVM分类器的决策边界,不
仅分离了两个类别,且尽可能远离最近的训练实例。
2.1 硬间隔
在上面我们使用超平⾯进行分割数据的过程中,如果我们严格地让所有实例都不在最⼤间隔之
间,并且位于正确的⼀边,这就是硬间隔分类。 硬间隔分类有两个问题,⾸先,它只在数据是线
性可分离的时候才有效;其次,它对异常值非常敏感。
当有⼀个额外异常值的鸢尾花数据:左图的数据根本找不出硬间隔,⽽右图最终显示的决策
边界与我们之前所看到的⽆异常值时的决策边界也⼤不相同,可能⽆法很好地泛化。
2.2 软间隔
要避免这些问题,最好使⽤更灵活的模型。⽬标是尽可能在保持最⼤间隔宽阔和限制间隔违
例(即位于最⼤间隔之上, 甚⾄在错误的⼀边的实例)之间找到良好的平衡,这就是软间隔分
类。 要避免这些问题,最好使⽤更灵活的模型。⽬标是尽可能在保持间隔宽阔和限制间隔违例之
间找到良好的平衡,这就是软间隔分类。
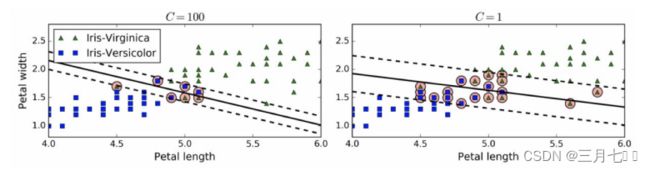
在Scikit-Learn的SVM类中,可以通过超参数C来控制这个平衡:C值越小,则间隔越宽,但是
间隔违例也会越多。上图显示了在⼀个非线性可分离数据集上,两个软间隔SVM分类器各自的决
策边界和间隔。 左边使用了高C值,分类器的错误样本(间隔违例)较少,但是间隔也较小。 右
边使用了低C值,间隔大了很多,但是位于间隔上的实例也更多。看起来第⼆个分类器的泛化效果
更好,因为⼤多数间隔违例实际上都位于决策边界正确的⼀边,所以即便是在该训练集上,它做出
的错误预测也会更少。
3. SVM的损失函数
在SVM中,我们主要讨论三种损失函数:
绿色:0/1损失
当正例的点落在y=0这个超平⾯的下边,说明是分类正确,⽆论距离超平⾯所远多近,误差都是0。
当这个正例的样本点落在y=0的上方,说明分类错误,⽆论距离多远多近,误差都为1。
图像就是上图绿色线。
蓝色:SVM Hinge损失函数
当⼀个正例点落在y=1的直线上,距离超平面长度1,那么1-ξ=1,ξ=0,也就是说误差为0。
当它落在距离超平面0.5的地方,1-ξ=0.5,ξ=0.5,也就是说误差为0.5。
当它落在y=0上的时候,距离为0,1-ξ=0,ξ=1,误差为1。
当这个点落在了y=0的上方,被误分到了负例中,距离算出来应该是负的,比如-0.5,那么1-
ξ=-0.5,ξ=1.5。误差为1.5。
以此类推,画在⼆维坐标上就是上图中蓝色那根线了。
红色:Logistic损失函数
当y = 0时,损失等于ln2,这样线很难画,所以给这个损失函数除以ln2,这样到y = 0时,损
失为1,即损失函数过(0,1)点,即上图中的红色线。
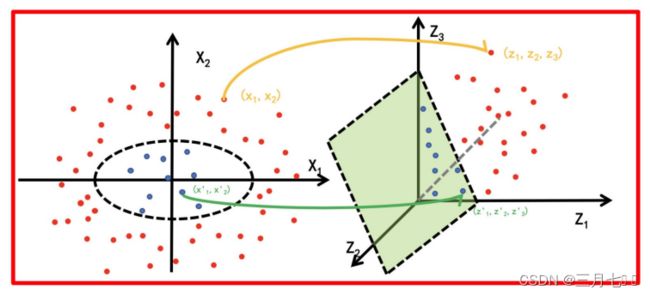
4. SVM的核方法
核函数并不是SVM特有的,核函数可以和其他算法也进⾏结合,只是核函数与SVM结合的优
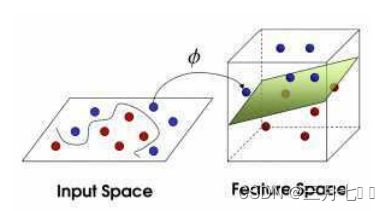
势非常⼤。核函数,是将原始输⼊空间映射到新的特征空间,从而,使得原本线性不可分的样本可
能在核空间可分。
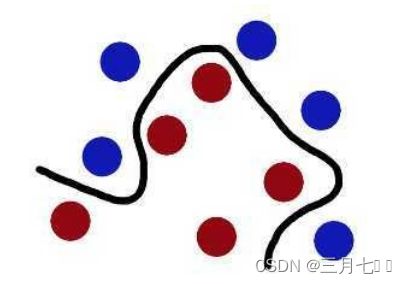
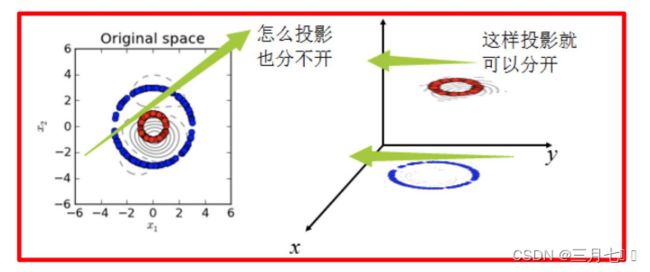
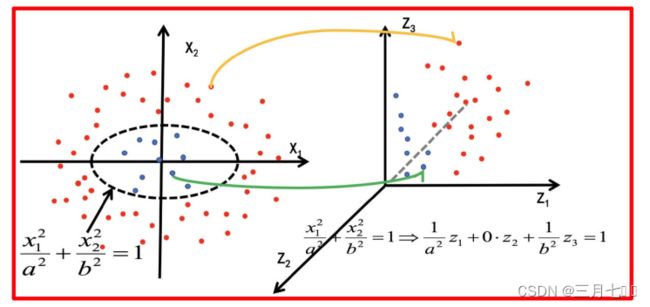
下图所示的两类数据,分别分布为两个圆圈的形状,这样的数据本身就是线性不可分的,此时
该如何把这两类数据分开呢?
假设X是输⼊空间, H是特征空间, 存在⼀个映射ϕ使得X中的点x能够计算得到H空间中的点
h, 对于所有的X中的点都成立:
若x,z是X空间中的点,函数k(x,z)满足下述条件,则称k为核函数,⽽ϕ为映射函数:
核方法案例1:
核方法案例2:
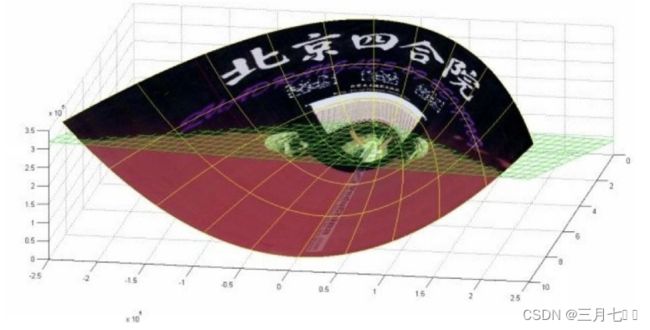
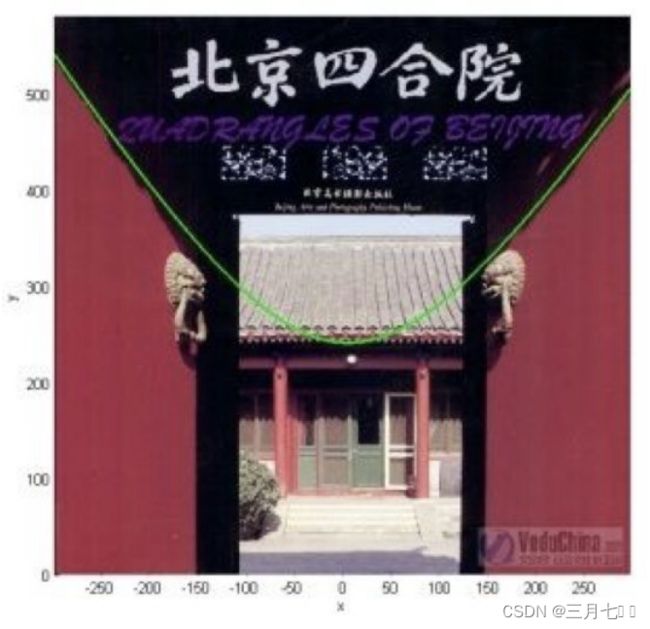
下⾯这张图位于第⼀、⼆象限内。我们关注红色的门,以及“北京四合院”这⼏个字和下面的紫
色的字母。 下⾯这张图位于第⼀、⼆象限内。我们关注红色的门,以及“北京四合院”这几个字和下
⾯的紫色的字母。
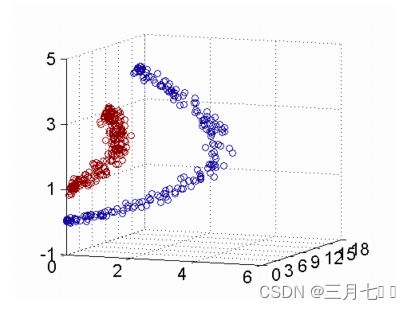
绿色的平面可以完美地分割红色和紫色,两类数据在三维空间中变成线性可分的了。 三维中
的这个判决边界,再映射回⼆维空间中:是⼀条双曲线,它不是线性的。 核函数的作用就是⼀个
从低维空间到高维空间的映射,⽽这个映射可以把低维空间中线性不可分的两类点变成线性可分
的。
常见的核函数:
2.高斯核亦称为RBF核。
线性核和多项式核:
这两种核的作用也是⾸先在属性空间中找到⼀些点,把这些点当做base,核函数的作用就是
找与该点距离和角度满足某种关系的样本点。
当样本点与该点的夹角近乎垂直时,两个样本的欧式长度必须非常长才能保证满足线性核函
数大于0;而当样本点与base点的方向相同时,长度就不必很长;而当方向相反时,核函数值就是
负的,被判为反类。即它在空间上划分出⼀个梭形,按照梭形来进⾏正反类划分。
RBF核:
高斯核函数就是在属性空间中找到⼀些点,这些点可以是也可以不是样本点,把这些点当做
base,以这些 base 为圆心向外扩展,扩展半径即为带宽,即可划分数据。 换句话说,在属性空
间中找到⼀些超圆,⽤这些超圆来判定正反类。
Sigmoid核:
同样地是定义⼀些base, 核函数就是将线性核函数经过⼀个tanh函数进⾏处理,把值域限制
在了-1到1上。 总之,都是在定义距离,⼤于该距离,判为正,小于该距离,判为负。至于选择哪
⼀种核函数,要根据具体的样本分布情况来确定。
⼀般有如下指导规则:
1) 如果Feature的数量很大,甚至和样本数量差不多时,往往线性可分,这时选用LR或者线
性核Linear;
2) 如果Feature的数量很小,样本数量正常,不算多也不算少,这时选用RBF核;
3) 如果Feature的数量很小,而样本的数量很大,这时⼿动添加⼀些Feature,使得线性可
分,然后选用LR或者线性核Linear;
4) 多项式核⼀般很少使用,效率不高,结果也不优于RBF;
5) Linear核参数少,速度快;RBF核参数多,分类结果⾮常依赖于参数,需要交叉验证或网
格搜索最佳参数,⽐较耗时;
6)应用最⼴的应该就是RBF核,⽆论是小样本还是⼤样本,高维还是低维等情况,RBF核函
数均适用。