编译原理（第二章2--正则表达式到NFA&DFA的转化）
目录
1.状态机引入
1.1 NFA定义
1.2 DFA定义
1.3 NFA & DFA 的差异
1.4 小结
2.正则表达式转NFA
2.1 转化规则
2.2 练习
3.NFA转DFA---子集法
3.1 -闭包
3.2 子集法定义
3.3子集法举例
3.3.1 练习一
3.3.2 练习二
3.3.1 练习三
4. 小结
1.状态机引入
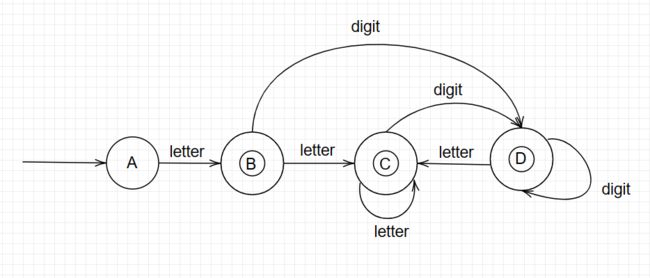
通过前面正则表达式的介绍，我们已经实现了把满足特定要求词法Token利用正则表达式表示出来，比如说我们可以很轻松地表示c语言的标识符如下：
letter -> a|b|...z|A|B|...|Z|_
digit -> 0|1|...|9
identifier -> letter(letter|digit)*那么现在的问题是咱们学会了这个有啥用？因为咱们构建词法扫描最终的目的是实现第一章提到的要求，那就是识别出源代码文本的的Token并将其输出，这需要用程序来实现。因此，我们发现正则表达式是无法满足我们的要求，所以我们需要进一步地引入状态机来编写程序，实现识别Token。
而状态机分为两种，一种是非确定有限自动机（NFA），一种是确定有限自动机（DFA）。
1.1 NFA定义
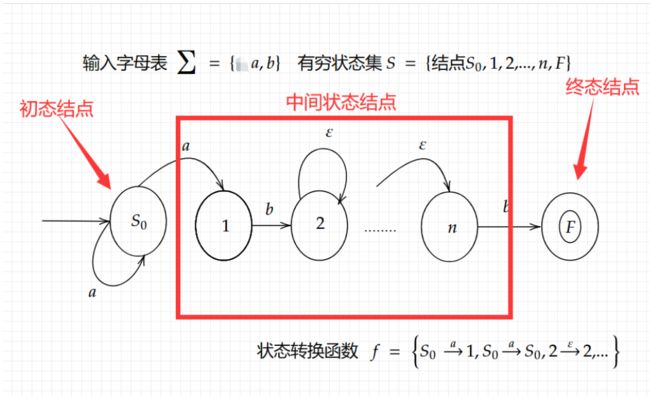
这里我们给出NFA定义如下：
看定义很复杂，其实很好理解。它就是用图的方式来表示正则表达式能表示的词法。它需要一个初态点和终态点以及两者中间若干的转化状态结点，同时需要箭头弧和其上面的字符来表示不同状态结点之间是如何转化的。
为了方便理解，举个简单的NFA图如下：
1.2 DFA定义
这里我们给出DFA的定义如下：
这里可以像理解NFA一样去理解DFA，它们是相似的，但却又有重要的差异。
1.3 NFA & DFA 的差异
两者的定义比较如下：
可以看出，第3条状态转化函数有着细微的区别。因此我们有：
- DFA要求转化函数单值部分映射，而NFA则只需要部分映射。这意味着DFA的状态给定，输入的字符给定，那末他的下一个状态一定是确定的，而不像NFA
- DFA不允许出现在弧上
- DFA要求弧上的输入必须是单个字符，而NFA的输入可以是一个字（而不强求是单个字符）
综上，我们知道DFA其实是一种特殊NFA。
1.4 小结
通过前面的介绍，我们了解了两个状态机NFA和DFA以及它们的区别。还记得我们引入状态机的目的吗？
因为正则表达式表示的词法我们无法用程序去实现，所以我们引入状态机。
现在，请思考一个问题，前面介绍的DFA和NFA我们选择哪种来转化？也就是说假如我现在已经有了一个关于C语言标识符的正则表达式，我将其最终转化成DFA还是NFA才能用程序编写实现呢？
答案是DFA。为什么?因为程序不能有二义性，我们需要一个给定状态和输入字符就能到达下一个唯一的状态，而这只有DFA才能办到。
但是在实际转化中，因为由正则表达式一步转成DFA是比较困难的，因此我们常常先将正则表达式转成NFA，然后再由NFA转成DFA。
2.正则表达式转NFA
2.1 转化规则
正则表达式转化成NFA的三条基础规则如下：
上述的核心是：要记住表达式中积、选择和闭包运算如何转化成对应的图。
2.2 练习
举个简单的例子，若有正则表达式如下,试画出其NFA图：
(ab|a)*画法如下：
- 画出初态和终态
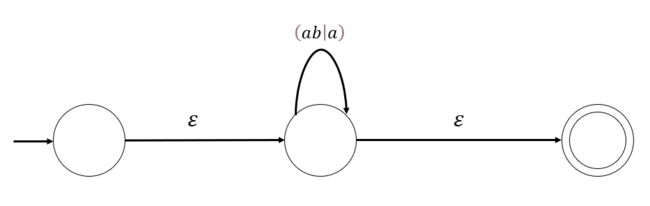
- 利用如下规则替换闭包
得到
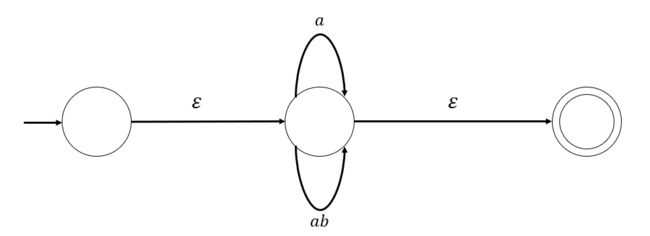
- 利用如下规则替换选择运算
得到
- 利用如下规则替换连接运算
得到：
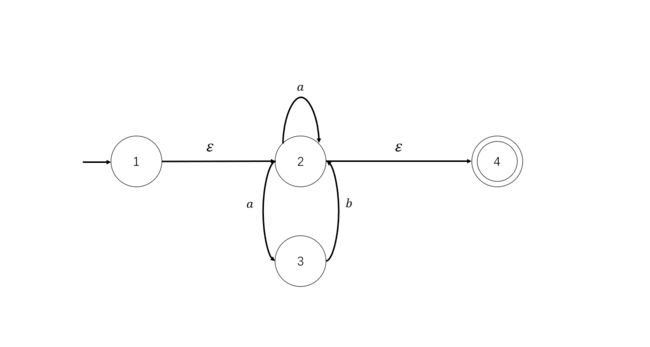
- 状态编号，得到NFA如下
正则表达式转成NFA是相对简单的，按照规则一步一步替代就行。
3.NFA转DFA---子集法
通过前面的转化，我们得到了一个NFA图，但是我们说过我们最终要的是DFA图，因此我们还要将NFA转成DFA。也就是要：
- 去除导致二义性的多重转化
- 去除
NFA转DFA，这里我们介绍一种常用的方法--子集法。
3.1 -闭包
这里我们先引入一个-闭包概念为子集法做铺垫。定义如下：
定义看起来很绕，其实很好理解，什么是 状态集I的-闭包（也就是-closure(I)）呢？两个点：
- 任何属于I中状态结点都在-closure(I)中
- 从任何属于I中的状态结点经过任意条输入字符为的弧能到达的结点都在-closure(I)中
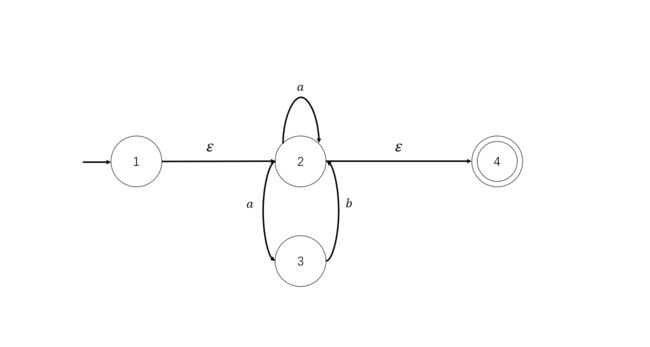
以上面我们求出的NFA为例：
试着找出其中-closure({1，2})。
根据上面解释的两个点来找：
- 任何属于I中状态结点都在-closure(I)中，故1，2是
- 从任何属于I中的状态结点经过任意条输入字符为的弧能到达的结点都在-closure(I)中
因为1∈{1，2}：从结点1走一条空弧到达2，从结点1走两条空弧到达4，故有 2，4
因为2∈{1，2}：从结点2走一条空弧到达4
综上：-closure(I) = {1，2，4}
3.2 子集法定义
通过前面的铺垫，我们有子集法的定义如下：
也就是：
（1）从M=初态结点S0开始，构建S = -closure({S0})
（2）先定义一个新的运算：
因此，对任意执行上述定义的新运算
(3)从上述新运算的结果中选择一个不曾出现在M中的集合的-closure令其为S
重复（2）直到没有新结果不曾出现在M中
(4)对每一个S重新定义一个状态，每个状态之间的连接字符很容易看出，这样就可以得到一个新的DFA图（注意包含原终态的新状态都是DFA的终态）
定义给人的感觉很绕，不好理解，这是必然的，因此我们通过几个例子来帮助理解。
3.3子集法举例
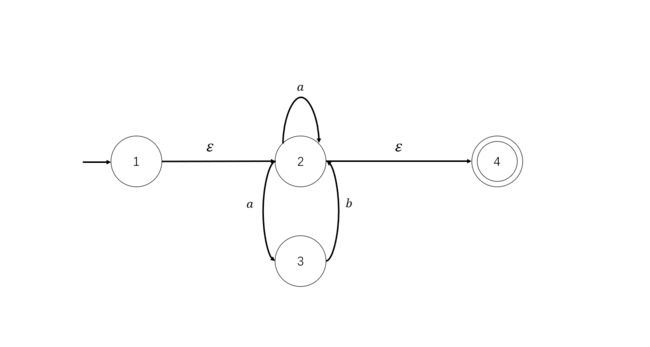
我们提供如下几个NFA图，请将其转化成DFA图：
3.3.1 练习一
根据上述算法：
（1）找到M = 初态结点1，构建S = -closure({1}) = {1，2，4}
（2）执行新运算
，过程如下：
对1∈S，1没有a输入的转换函数
对2∈S，2有a输入的转换函数，2经过输入a到达3
对3∈S，3没有a输入的转换函数
而字母表中只有a，所以算法的步骤2结束；
对于上述过程，我们有记录表格如下：
（3）从新的运算结果中选取不曾在M中出现的集合计算-closure并复制为S。
这里因为新的运算结果只有{3}，且没有在M中出现过，所以选择{3}计算-closure赋值为S，重复执行（2）则有：S = -closure({3}) = {2，3，4}
执行新运算，过程如下：
对2∈S，2有a输入的转换函数，2经过输入a到达3；
对3∈S，3没有a输入的转换函数；
对4∈S，4没有a输入的转换函数。
对于上述过程，我们有记录表格如下：
此时转到（3），从新的运算结果中选取不曾在M中出现的集合计算-closure并复制为S。而我们发现全部新的运算结果{3}在M中都曾出现，也就是说没有新的状态产生。则跳出重复，执行（4）
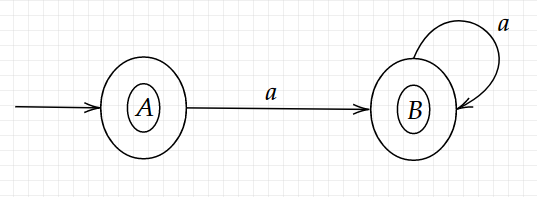
（4）对每一个S重新定义一个状态,不妨令：
A = {1,2,4}
B = {2,3,4} 每个状态之间的连接字符很容易看出，这样就可以得到一个新的DFA图。也就是说我们通过
可以看出从A经过输入字符a可以到达3对应的状态B，从B经过字符a可以到达3对应的状态B。我们在算法中说了，包含包含原终态的新状态都是要构建的DFA的终态。而上述结果A、B都包含了原来的终态4，因此A、B都是终态（同心圆表示）。所以我们可以作上述NFA对应的DFA如下：
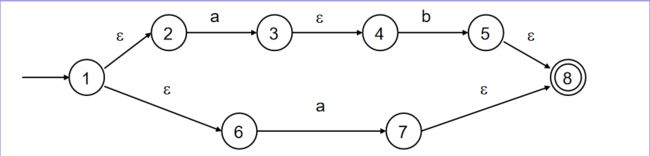
3.3.2 练习二
同理，根据上述算法：
（1）找到M= 初态结点1，构建S = -closure({1}) = {1,2,6}
（2）执行新运算，注意这里字母表包含a，b。因此我们要执行
（2-1）执行，过程如下：
对于1∈S，1没有a输入的转换函数
对于2∈S，2有a的输入转换函数，经过a到达3
对于6∈S，6有a的输入转换函数，经过a到达7
记录表格如下：
（2-2）执行
,过程如下：
对于1∈S，1没有b输入的转换函数
对于2∈S，2没有b输入的转换函数
对于6∈S，6没有b输入的转换函数
记录表格如下：
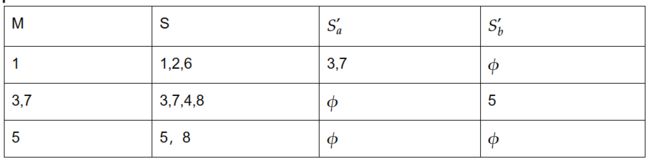
(3)在新的运算结果中选出不曾在M中出现的集合{3，7}，计算 -closure({3，7}) = S，记录表格如下：
转到（2）步骤去执行新运算，得到结果如下：
再经过（3）挑选出{5}，计算-closure({5}) = S，再次跳转到（2）执行新的运算，得到结果如下：
新的运算结果为空集，故终止（3），进入（4）
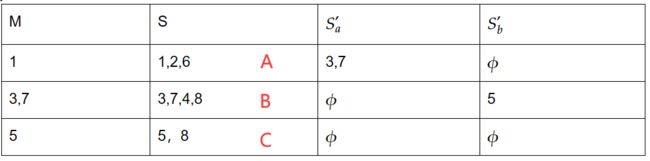
（4）重新命名状态（注意终态的存在）
可以看出：
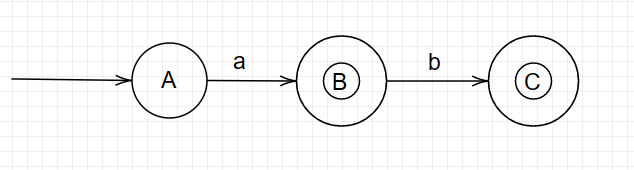
A经过a到达B，B经过b到达C,终态为B、C
故有DFA如下：
3.3.1 练习三
练习三，直接给出答案，读者可以自己尝试去写出过程：
NFA如下：
记录表格如下：
替换状态如下：
DFA如下：
4. 小结
本文介绍了为什么在正则表达式的基础上还需要状态机（为了编写程序），剖析了两种状态机NFA和DFA以及它们之间的区别。更重要的是，本文介绍了如何由正则表达式画NFA，再由NFA通过子集法画对应的DFA。
理论上来说我们现在就可以利用程序来实现DFA表达的词法特点，如何用程序来实现呢？我们将在下一篇文章介绍。