前缀和、树状数组和线段树的区别
2023.2.3对树状数组部分增加了内容,因为原文章markdown语法不太兼容所以重新发表
2023.2.6增加文章目录,对不合理的目录等级进行了修改
文章目录
- 前缀和:
-
- 简洁构造
- 树状数组:
-
- lowbit(最低位)
- 建树
-
- 1. O(nlogn)建树:就是对每个点单点更新
- 2. O(n)建树:
- 单点修改
- 区间查询
-
- 正常查询
- 优化查询
-
- 原理
- 线段树:
-
- 细节
- update更新
- push_down传递
- add_tag打标记

前缀和:
一般用于固定数组。可以区间求和
简洁构造
a = list(map(int, input().split()))
s = [0]
for i in range(n):
s.append(s[-1]+a[i])
树状数组:
非常高效的数据结构,可以满足大部分需求。可以区间求和、区间最大值、单点修改。一般不能区间修改(就这个结构而言)
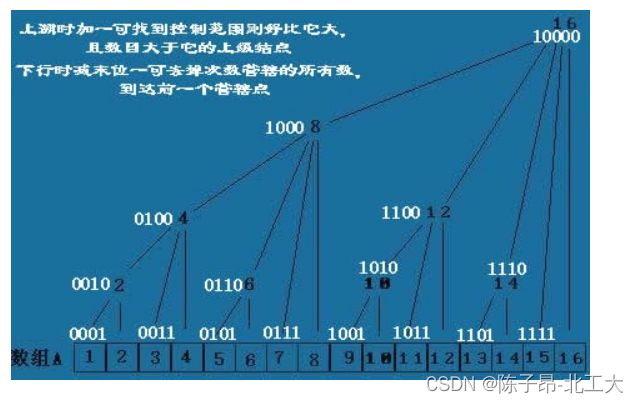
lowbit(最低位)
- 是二进制从右向左的第一个1,即最低为的1.如6的二进制是110,所以返回的是2
图片出处:树状数组(求逆序对)_baby的我的博客-CSDN博客_树状数组求逆序对已征得原作者的同意使用此图。
建树
1. O(nlogn)建树:就是对每个点单点更新
2. O(n)建树:
code1(利用前缀和:会浪费空间)
for i in range(1, n):
tr[i] = d[i] - d[i-lowbit(i)] # d是前缀和数组, 因为lowbit(i)就是tr(i)维护的原数组的长度
原本nlogn就是因为有重复计算的数组,那么只要把已经建好的部分直接累加到后面就可以保证每个都只计算一次,即O(n)
code2
for i in range(1, n):
tr[i] = a[i]
j = 1
flag = lowbit(i) # 对应上面的图,每个数字下面连的就是要加上去的
while j < flag:
tr[i] += tr[i-j]
j <<= 1
code3首推(简洁)
for i in range(1, n):
tr[i] += a[i]
if (fa := i+lowbit(i)) <= n:
tr[fa] += tr[i] # +最低位变父亲,-最低位变儿子
code2\3先进的地方就在于不是利用a来推,而是利用已经建好的树,避免了a的重复叠加。code2和code3进行操作的次数一定是一样的,code2看起来多但是有些节点甚至是没子结点的
单点修改
def add(x, k):
while x <= n:
tr[x] += k
x += lowbit(x)
区间查询
正常查询
def query(x):
ans = 0
while x:
ans += tr[x]
x -= lowbit(x)
print(query(j)-query(i-1))
优化查询
def query(x, y):
"""对区间和而言是[x+1, y], 因为到x都被减掉了"""
ans = 0
while y > x:
ans += tr[y]
y -= lowbit(y)
while x > y:
ans -= tr[x]
x -= lowbit(y)
原理
- 完全避免了重复部分的计算,比如查询[6, 7](一定要注意这样写和原始的都是对应7-5,左边界始终差了一位),则需要计算([7]+[6]+[4])-([5]+[4]) ,其中[4]就是重复的
- 以上面为例5:101,7:111。两个同时抹掉最后一位,不相等,再抹掉倒数第二位,两个相等了,不用再计算了,必定消掉
- 但是一位一位算就失去了lowbit的优势,所以采取两个互相逼近的方式,能一直取到两个相等
- 这样一定不会抹到开头相同的部分,因为到相同的部分一定小于或相等
线段树:
非常灵活的数据结构。可以区间求和、区间最大值、区间修改、单点修改。
细节
- 树要开四倍空间:假设最后一行的叶子节点个数为n,倒数第二行的叶子节点个数为m,则节点数是2(n/2+m)-1+m=2N-1, N是数组数量,但是开2倍还是不够的,因为在偏向均分的情况下,有一些节点是在右子树的,而左子树还没满,也就导致了中间序号被跳过了。那么我们直接把最后一层填满以绝后患。即2(m*2+n)-1=4N-2n-1.开四倍空间绝对不会有越界的情况并且不用+1。也可以根据dfs序直接使用2N-1的空间,但是这样遍历的时候左右孩子的索引变得难以确定。在空间缩小一半的情况下时间效率大概降低了 10%~15% 左右,且进行 down 下传的时候变成不容易操作,酌情使用!
update更新
def update(L,R,p,pl, pr, d) :
if L<=pl and R>=pr: # 某区间的子树都包含在这个区间里,这样取可以全部取到
add_tag (p, pl, pr,d)
return
push_down(p,pl, pr) # 将懒惰标记传递给孩子(在前面标记过且这次有不包含在里面的元素)
mid = pl + pr >> 1
if L <= mid:
update(L,R,p << 1,pl, mid, d)
if R >= mid + 1:
update(L,R, p << 1|1, mid+1, pr,d)
tree[p] = tree[p << 1] + tree[p << 1|1] # push_up(p)
因为某区间的子树都包含在这个区间里,所以不包含的区间一定都是不包含的,这样在if L<=pl and R>=pr 时就可以取到所求区间里的所有部分。
push_down传递
def push_down(p, pl, pr):
if tag[p]>0: # 有tag标记,这是以前做区间修改时留下的,相当于延时标记
mid = pl+pr >> 1
add_tag (p<<1,pl,mid, tag[p]) # 把tag标记传给左子树
add_tag (p<<1|1,mid+1, pr, tag[p]) # 把tag标记传给右子树tag[p]=0
#p自己的tag被传走了,归0
push_down相当于延迟标记,在要用到的时候向下传。但是push_down是单次的,要借用update的递归才能一层一层向下传递,直到能覆盖区间。到能覆盖的节点,懒标记还在,但是懒标记的值是上一次传递的(相当于值只传递到本次要用的地方,后面不再传递)。本次更新的值在后面会进行叠加
add_tag打标记
懒标记实质:只计算出确实需要访问的区间的真实值,其他的保存在lazytag里面,这样可以近似O(nlogn)的运行起来。
def add_tag (p, pl, pr, d) :
"""给结点p打tag标记,并更新tree"""
tag[p] += d # 打上tag标记。并不是等于d是因为可能有上次的懒标记传递
tree[p] += d*(pr-pl+1) # 计算新的tree