【雷达原理】雷达杂波抑制方法

目录

一、杂波及其特点

1.1 什么是杂波？

1.2 杂波的频谱特性

二、动目标显示(MTI)技术

2.1 对消原理

2.2 数字对消器设计

三、MATLAB仿真

3.1 对消效果验证

3.2 代码

---

一、杂波及其特点

1.1 什么是杂波？

杂波是相对目标回波而言的，它是指对雷达正常工作时的目标回波有干扰的回波信号。对于工作在地面的雷达，杂波主要来源于固定建筑物、围栏、树木等静止目标或慢速运动目标产生的回波以及地表反射的回波。

由于单个杂波分量具有随机的相位和幅度，因此合成的总杂波也是随机的，具有类似热噪声的统计特性，并且杂波信号的强度要远大于接收机内热噪声的强度。因此，雷达在强杂波背景下检测目标的能力主要取决于信杂比，而不是信噪比。

杂波抑制的目的就是采用数字信号处理技术滤除或者抑制固定目标杂波和慢速目标杂波，从而保留运动目标回波。

1.2 杂波的频谱特性

雷达工作时可能会碰到的杂波包括地物、海浪、云雨及敌人施放的箔条等。除了孤立的建筑物可认为是固定的点目标外，大多数杂波均属于分布杂波且包含内部运动。当天线不扫描时，固定杂波的功率谱是位于(n=0，±1，±2，...) 位置上的离散谱线，其中为脉冲重复频率。当天线扫描时，由于回波脉冲数有限，将引起谱线的展宽。此外，由于天线扫描引起双程天线方向图对回波信号调幅，也会导致功率谱展宽。

一般杂波谱可用高斯函数表示为：

其中，，n为单程天线方向图3dB宽度内的脉冲数。

二、动目标显示(MTI)技术

2.1 对消原理

当固定目标、地杂波等与运动目标处于同一距离单元时，前者的回波通常较强，以至于运动目标的回波被淹没其中，故必须设法对二者进行区分。

因固定目标回波的多普勒频率为零，慢速运动的杂波中所含的多普勒频移也集中在零频附近，它们的回波经相位检波后，输出信号的相位将不随时间变化或者不随时间做缓慢变化，反映在幅度上则为其幅度不随时间变化或者不随时间做缓慢变化。相反运动目标回波经相检输出后，因其相位随时间变化较大，反映在幅度上也是幅度随时间变化较快。

因此若将同一距离单元在相邻重复周期内的脉冲做相减运算，则固定目标回波将被完全对消，慢速杂波也将得到很大程度的衰减，只有运动目标回波得以保留。这样就可以将固定目标、慢速目标与运动目标区别开来。

2.2 数字对消器设计

数字对消器本质上就是一种数字滤波器，根据所设计滤波器的幅频响应特性，可以滤除相应频率的信号分量。常用的MTI滤波器为延迟线对消器，根据对消次数的不同，可分为单延迟线对消器、双延迟线对消器和多延迟线对消器。

1、单延迟线对消器

1-1 单延迟线对消器结构图

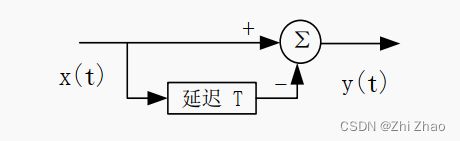
 单延迟线对消器的结构如图1-1所示，滤波器的输出为输入的两个脉冲进行运算得到，该滤波器也称为双脉冲对消器或者一次对消器，其用数学公式可表示为：

其中，T为脉冲重复周期PRT。

对上式求Z变换，可得：

由此可知其系统函数为：

由傅里叶变换与Z变换的关系，，得到对消器的功率增益为：

进而得到其幅频响应为：

单延迟线对消器的幅频响应曲线如图1-2所示，取脉冲重复周期，则脉冲重复频率，由滤波器的幅频特性曲线可知，在频率处有零点，因而该滤波器起到了抑制固定目标回波和慢速运动目标回波的作用。

1-2 单延迟线对消器的幅频响应

2、双延迟线对消器

2-1 双延迟线对消器结构图

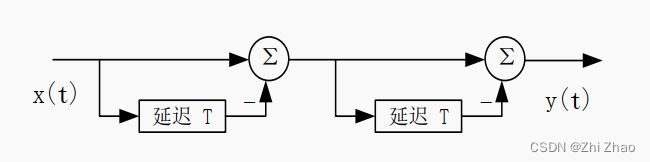
 双延迟线对消器的结构如图2-1所示，它由两个单延迟线对消器级联而成。双延迟线对消器经常被称为三脉冲对消器或者二次对消器，其数学表达式如下：

对上式求Z变换，可得：

由此可知其系统函数为：，从系统函数的表达式可以看出其等效于两个一次对消器级联。

由此得到二次对消器的功率增益为：

式中，为单延迟线对消器的功率增益。

进而得到其幅频响应为：

双延迟线对消器的幅频响应曲线如图2-2所示，可以看出，双延迟线对消器比单延迟线对消器具有更好的响应(更深的凹口和更平坦的通带响应)。单延迟线对消器的频率响应较差，原因在于其阻带没有宽的凹口。而双延迟线对消器无论在阻带还是通带上都比单延迟线对消器有更好的频率响应，因此得到了更广泛的应用。

2-2 延迟线对消器的幅频响应

3、多延迟线对消器

3-1 多延迟线对消器

多延迟线对消器的结构如图3-1所示，它是由多个单延迟线对消器级联而成，N延迟线对消器的数学表达式为：

式中，N为对消器的次数，对消器的系数为二项式系数，用下式计算：

N次对消器的系统函数可表示为：

其幅频响应和相频响应分别为：

可见，相位响应φ(w)与w是线性关系，所以对消器是一种线性相位滤波器，回波信号通过它后，相位关系不产生非线性变化。

三、MATLAB仿真

3.1 对消效果验证

由第二节的内容可知，MTI技术实质上就是设计一个滤波器，通过对多组脉冲回波的同一个距离单元加权求和即可实现。对于静止目标在该距离单元频谱固定，加权求和后将固定的频谱相互抵消；对于运动目标在该距离单元频谱存在多普勒频移，加权求和后目标频谱不会完全抵消。

通过MATLAB仿真多组具有静止目标和运动目标的回波信号，对比不同次数的对消器对杂波的抑制效果。
案例及对应的代码会在博文【雷达测速原理及实现方法】写完后更新。

3.2 代码

clc;
clear;
close all;

%% 单延迟线对消器
PRT = 1e-3;
PRF = 1/PRT;
f = (-2000:1:2000);
H1 = 2*abs(sin(pi*f*PRT));
H1 = H1/max(H1);
H1_d = mag2db(H1);
figure;
subplot(2,1,1);plot(f/PRF,H1);
xlabel('归一化频率f/fr');ylabel('幅度');title('延迟线对消器的幅频响应');
subplot(2,1,2);plot(f/PRF,H1_d);
xlabel('归一化频率f/fr');ylabel('幅度(dB)');ylim([-50 0]);

%% 双延迟线对消器
H2 = 4*abs(sin(pi*f*PRT)).^2;
H2 = H2/max(H2);
H2_d = mag2db(H2);
figure;plot(f/PRF,H1_d);hold on;plot(f/PRF,H2_d);ylim([-50 0]);
xlabel('归一化频率f/fr');ylabel('幅度(dB)');title('延迟线对消器的幅频响应');
legend('单延迟线对消器','双延迟线对消器');