宏观经济学 IS-LM模型

总需求

曲线：产出需求量与价格水平之间的关系，即$MV=PY$中，MV均为常数时

PY成反比

Y表示总需求

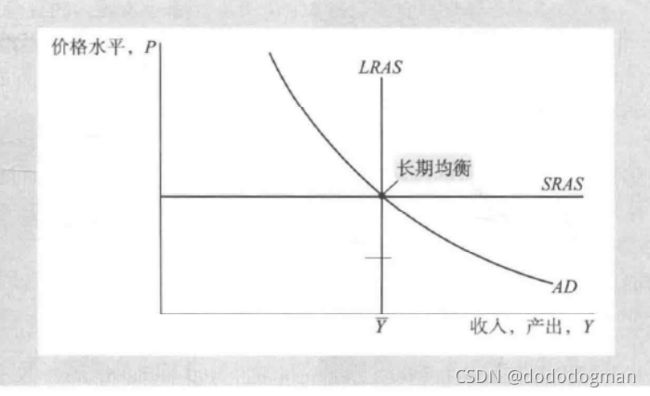
总供给

产品与服务的供给量与价格水平之间的关系

古典模型中：$Y=F(\bar{K},\bar{L})=\bar{Y}$

长期：供给曲线是垂直的，因为其产出水平由上述公式决定，而不随价格变动

短期：供给曲线是水平的，因为其价格是黏性的，不随产出的变动而变化

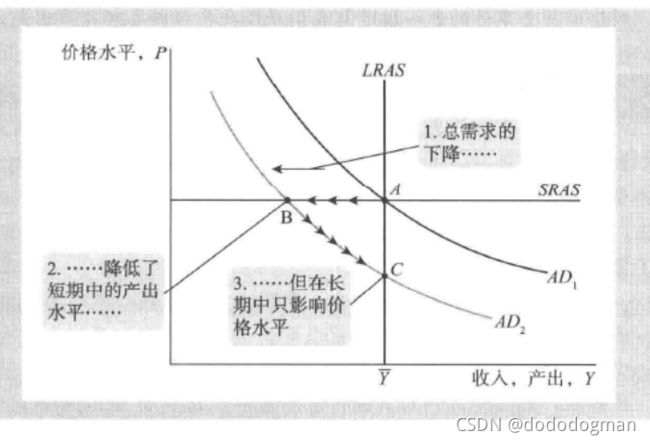
应用

综上，均衡时为下图这样

货币供给减少时：

冲击

对于总需求的冲击，以信用卡的大量使用为例：
每美元持有货币比例下降：k减小 $\to$ V=1/k增大，总需求曲线外扩：

凯恩斯交叉

$PE=C+I+G$

消费函数$C=C(Y-T)$代入：

$PE=C(Y-\bar{T})+\bar{I}+\bar{G}$

PE 计划支出
C消费
Y收入
Tbar 固定的税收水平（只是为了简化）
Ibar 固定的投资（假设）
Gbar 固定政府购买（假设）

斜率为边际消费倾向 MPC ：每一美元收入中计划用于支出的数额

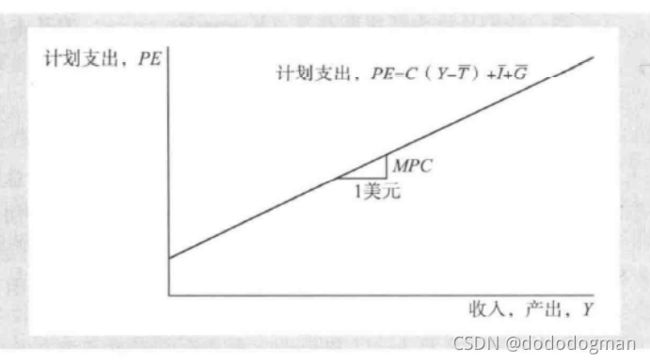
实际支出就是Y

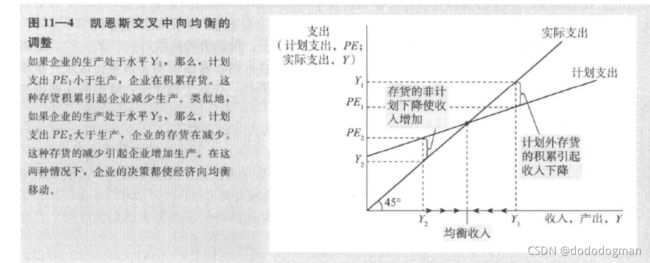
当实际支出与计划支出相等时，认为达到凯恩斯均衡

凯恩斯的均衡用存货投资解释

下图的交点即为凯恩斯交叉

凯恩斯均衡的调整过程

以上，描述在$\bar{I},\bar{G},\bar{T}$固定情况下，收入Y的决定

下面，分别讨论三个协变量分别变化的情况

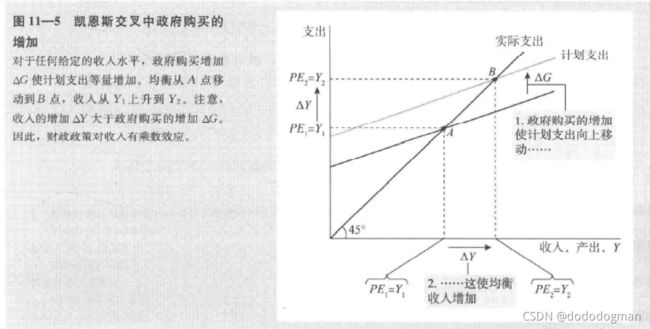
$\frac{\Delta Y}{\Delta G}=\frac{1}{1-MPC}$称为 政府购买乘数

$\frac{\Delta Y}{\Delta T}=-\frac{MPC}{1-MPC}$称为 税收乘数

注意，这里是每单位税收减少引起的收入变化，而不是收入本身变化，要乘MPC

上图为斜率为1/2的情况，一般情况的图不是这样的

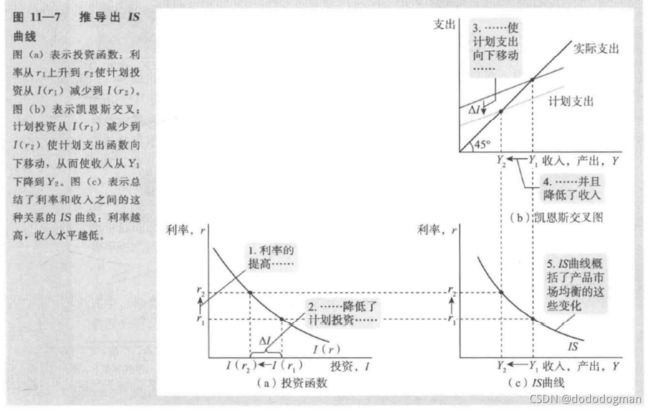
IS曲线

描述产品市场上利率与收入水平之间的关系

$I=I(r)$  图(a)

IS曲线上每一点都是 产品市场 均衡点

其实就是将两个图的不同轴分别画在了一起，形成一个新的函数关系图

当利率不变，政府政策变化时，IS曲线的变化

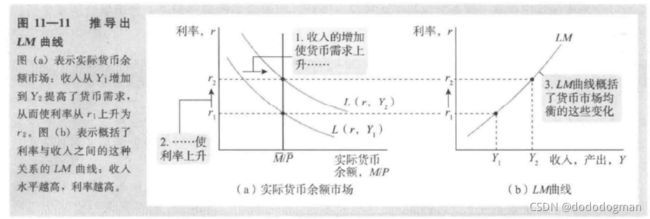
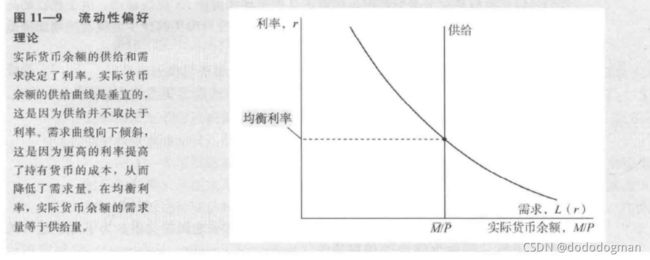
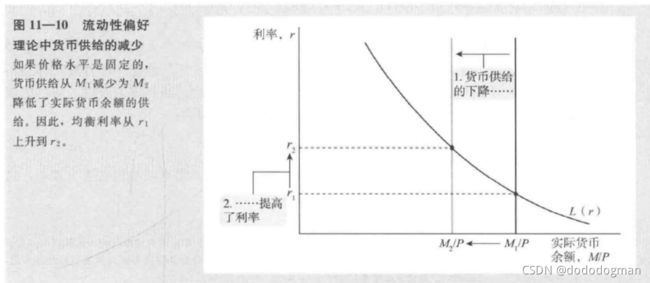
流动性偏好理论

利率是持有货币的机会成本
假设 M，P 固定，即货币余额固定
实际货币余额需求 $(M/P{)}^d=L(r)$
收入增加曲线外扩
每一点都是 货币市场 的均衡

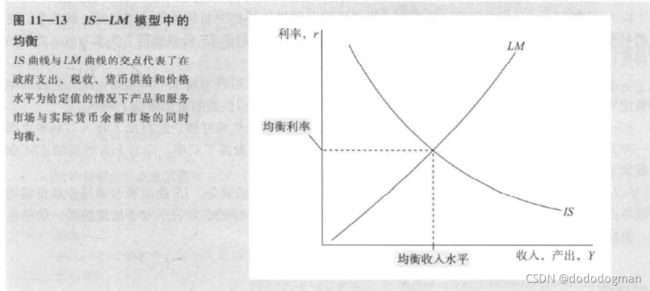
IS-LM模型

$Y=C(Y-T)+I(r)+G$

$M/P=L(r)$

两条线的交点为均衡点，此点 计划支出等于实际支出，货币余额的供给等于需求

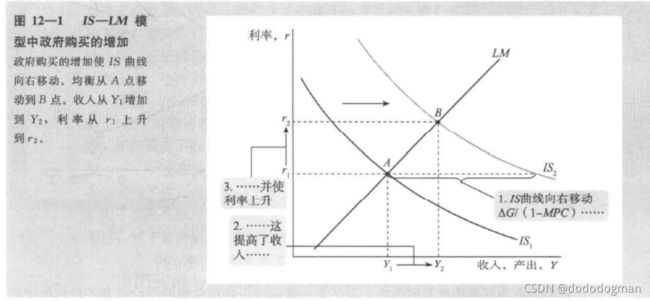
政府购买增加的变化
因为利率的增加，使得投资缩紧，导致凯恩斯交叉的收入变化量大于islm模型模型的变化量

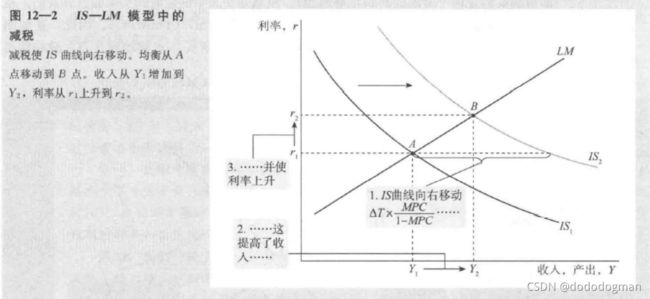
减税的变换
同样，利率上升投资缩减，两种变化量不同

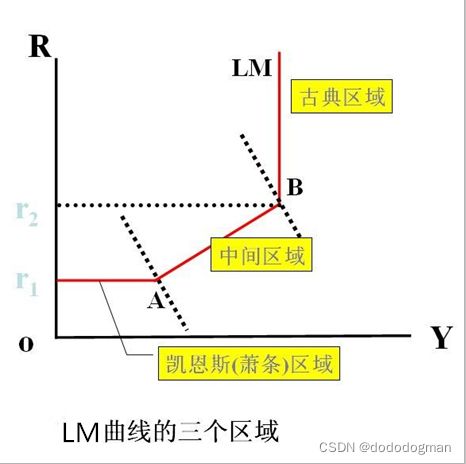
LM曲线上斜率的三个区域分别指LM曲线从左到右所经历的水平线、向右上方倾斜线、垂直线的三个阶段。LM曲线这三个区域被分别称为凯恩斯区域、中间区域、 古典区域 。

1、凯恩斯区域：利率降到很低（r1水平），货币的投机需求趋于无限大，货币投机需求曲线会成为一条水平线，相对应的LM曲线上也有一段水平状态的区域，这一区域通常就是我们说的凯恩斯区域。

在凯恩斯区域中，因为较低的利率水平，假设政府实行扩张性货币政策，增加货币供给，不能降低利率，也不能增加收入，因而货币政策在这时无效。相反，扩张性财政政策，可以使收入水平在利率不发生变化情况下提高，因而财政政策有很大的效果。

2、古典区域：如果利率上升到很高水平时候（r2水平），货币投机需求曲线表现为r2以上是一条与纵轴相重合的垂直线，LM曲线也从利率为r2开始成为一条垂直线。LM曲线呈垂直状态的这一区域就被称为古典区域。

这时候人们除了为完成交易还必须持有一部分货币外，不会为投机而持有货币。这时，扩张性财政政策完全失效，而扩张性货币政策则十分有效。

3、中间区域：古典区域和凯恩斯区域之间这段LM曲线是中间区域，LM曲线的斜率在古典区域为无穷大，在凯恩斯区域为零，在中间区域为正值。

这一阶段货币政策和财政政策都有效。