二叉树的三种遍历（先序中序后序）——递归非递归算法

回忆

在上一个关于树的博客提到了二叉树的三种遍历方式，还有一个单独的层次遍历。
先序、中序、后序本质山就是根、左、右的顺序问题
先序：根左右
中序：左根右
后序：左右根

递归算法

因为二叉树的定义（其实应该说树的定义）里面有递归的影子：每一个子树也要符合上述条件
（具体参见上一篇博客）
所以递归算法应该是最先想到的，而且因为递归的性质，函数形式也是最简单的。

先序：

void PreOrder(btree* bt)
{
    btree *p=bt;
    if(p)
    {
        cout <<p->data<< " ";
        PreOrder(p->lchild);
        PreOrder(p->rchild);
    }
}

中序：

void InOrder(btree* bt)
{
    btree *p=bt;
    if(p)
    {
        InOrder(p->lchild);
        cout << p->data<< " ";
        InOrder(p->rchild);
    }
}

后序：

void PostOrder(btree *bt)
{
    btree *p=bt;
    if(p)
    {
        PostOrder(p->lchild);
        PostOrder(p->rchild);
        cout << p->data<< " ";
    }
}

在阅读了这几个函数之后，应该会发现一个问题，就是在判断结点非空之后，对该节点、左孩子、右孩子的操作顺序进行改变就能实现不同的遍历。
确实如此，因为对于递归形式，只需要改变左中右的顺序即可。

非递归

因为每一次都要处理两个孩子结点（可能没有，但也要判断），所以需要暂时将这个结点存一下，而有存储功能的只有栈和队列；
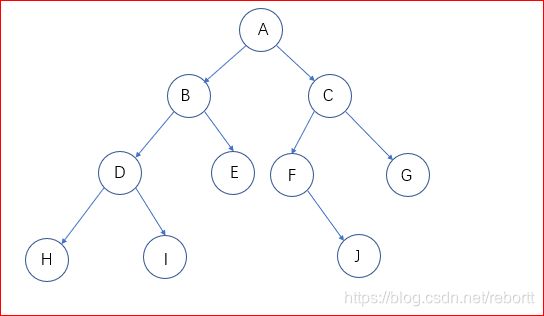
再分析一下，对A点，要先存储A，然后走到B，再处理B的左子树，存储D，然后存储H，H为叶子，需要回退，此时应该是D，然后依次走上去，所以我们这里应该用的是栈

准备阶段

struct link//栈
{
    btree* data;
    struct link* next;
};

void input_zhan(struct link* head,btree* data)//入栈
{
    struct link* p=(struct link* )malloc(sizeof(struct link));
    p->data=data;
    p->next=head->next;
    head->next=p;
}

btree* output_zhan(struct link* head)//出栈
{
    struct link* p=head->next;
    btree* ret=head->next->data;
    head->next=p->next;
    free(p);
    return ret;
}

因为不会发生空栈出栈的情况，所以没有判断。（zhan==栈。。。。）

先序：

void unPreOrder(btree* bt)
{
    struct link* head=(struct link* )malloc(sizeof(struct link));
    btree* p=bt;
    head->next=NULL;
    while(head->next||p)
    {
        if(p)
        {
            cout << p->data<< " ";
            input_zhan(head,p);
            p=p->lchild;
        }
        else
        {
            p=output_zhan(head);
            p=p->rchild;
        }
    }
    cout<<endl;
}

思路还是比较清晰的，先处理根节点，如果有左孩子就走，不然回退走右孩子，标准中左右。

中序：

void unInOrder(btree* bt)
{
    struct link* head=(struct link* )malloc(sizeof(struct link));
    btree* p=bt;
    head->next=NULL;
    while(head->next||p)
    {
        if(p)
        {
            input_zhan(head,p);
            p=p->lchild;
        }
        else
        {
            p=output_zhan(head);
            cout << p->data << " ";
            p=p->rchild;
        }
    }
    cout <<endl;
}

中序和先序差不多，就是将输出根节点放在了回退那一步，保证为左中右。

正常到了这里，会不会感觉后序也是单纯改一下顺序就行了呢？
不行，因为在退出之后不能直接输出，而是要将右子树遍历结束才行，要是遍历了右子树，如果正常存储早不知道根节点哪去了。。。

代码：

void unPostOrder(btree *bt)
{
    struct link* head=(struct link* )malloc(sizeof(struct link));
    btree* p=bt;
    head->next=NULL;
    
    do{
        while(p)
        {
            input_zhan(head,p);
            p=p->lchild;
        }
        
        int judge=1;//标识符
        btree* pr=NULL;//pr记录上一个输出
        
        while(head->next && judge)
        {
            p=head->next->data;//栈顶元素
            
            if(p->rchild==pr)//右子树不存在或者已经访问
            {
                cout<<p->data<< " ";
                p=output_zhan(head);
                pr=p;
            }
            
            else//指向右子树，开始遍历并退出循环
            {
                judge = 0;
                p=p->rchild;
            }
        }
    }while(head->next);
    cout <<endl;
}

和之前的代码差距还是比较大的，从头分析一下吧。

• 首先还是正常的往最左边走，直到为空。
• 需要回退，而且可能不止一次回退，直到找到一个合适的右子树，所以设置标识符judge（找到合适的右子树就置为0，退出循环）
• 回退的标准应当为右子树为空或者是已经访问过了，这个没什么，那么如何判断是否访问过，我们就需要将访问过的结点记录下来（当然不需要每一个都记录，最后一个就行了，因为最后一个结点要么是右孩子结点，要么没有右子树，则来自左子树）
• 当栈顶为空，也就是连根节点都出去了，循环结束。

这里面的退栈操作是为了贴合上面的函数，因为有返回值要是空着不好看，当然也可以把函数改成void型，对后序没影响。

对后序的一些神奇操作

根据之前我们可以知道，只要是保证了左右根的顺序，就能得到一个后序结果，那么我们已经有了根左右，那是不是我们可以修改一下先序的左右子树：

将p=p->l/r+child两项反过来，得到根右左
按照之前的理论，根右左和左右根互相是反过来的，只需要用一个栈将结果反着输出，就能得到后序遍历。
当时在dl的博客里面看到的，思路很独特但可能不太好想，亲测有效。

这个操作也说明了二叉树的递归性质，只要将左右子树的遍历反过来，就能从先左的遍历方式到先右的遍历方式（这里默认的方式都是先左子树）