机器学习2.1-2.7——单变量线性回归
模型描述
例子
以监督学习中的线性回归为例
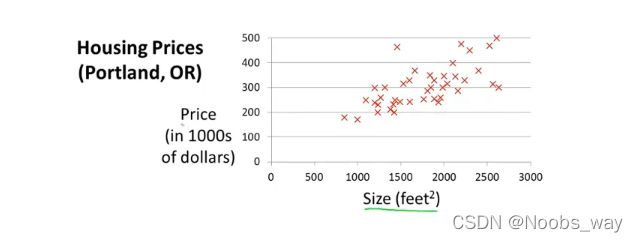
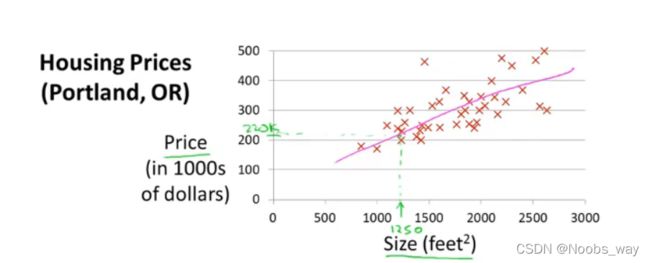
上图描述的是房屋尺寸和售价的关系。假如现在需要预测1250 f e e t 2 feet^2 feet2的房子售价,该如何建立模型?
上图数据似乎具有明显的线性趋势,因此我们可以使用一条直线来预测其走向。
术语标记
| 符号 | 术语 |
|---|---|
| x | 变量,特征 |
| y | 函数值,输出值,目标变量 |
| m | 样本个数 |
流程简介

我们将训练集的数据传递给算法,然后根据算法生成的假设函数进行预测,即输入房屋面积x,得出价格y。
在这个例子中,如前文所述,我们使用一个一次函数模型来进行房价预测。所以假设函数形式规定如下:
h θ ( x ) = θ 0 + θ 1 x h_\theta (x) = \theta_0 + \theta_1x hθ(x)=θ0+θ1x
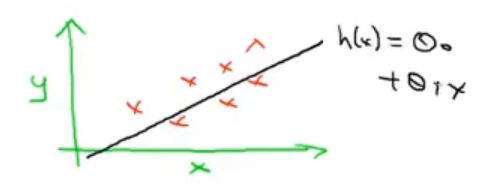
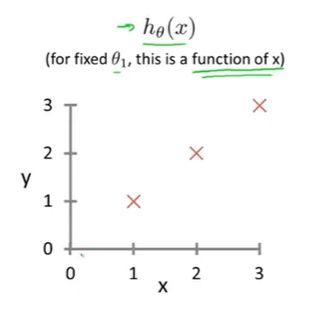
上图展示了y和 h θ h_\theta hθ的关系,又因为 h θ ( x ) = θ 0 + θ 1 x h_\theta (x) = \theta_0 + \theta_1x hθ(x)=θ0+θ1x的关系,所以我们把这种模型称为线性回归。
代价函数
参数选择
不同的 θ 0 \theta_0 θ0和不同的 θ 1 \theta_1 θ1会直接影响拟合结果,下图展示了选择不同的 θ 0 \theta_0 θ0和不同的 θ 1 \theta_1 θ1时函数形态。

通过选择不同的 θ 0 \theta_0 θ0和不同的 θ 1 \theta_1 θ1使得拟合结果更为精确,即使得各个样本真实值y和估计值 h θ ( x ) h_\theta (x) hθ(x)之间的差距较小,我们引入一个表达式来刻画这样的误差。
第i个样本的差距定义为:
Δ J i = ( h θ i − y ) 2 \Delta J_i = (h_\theta i - y) ^2 ΔJi=(hθi−y)2
将其求和后即为样本的总误差,然后平均后即为样本的平均误差:
Δ J = 1 2 m ∑ i = 1 m ( h θ i − y ) 2 \Delta J=\color{red} \frac{1}{2m}\color{black} \sum_ {i=1}^m(h_\theta i - y) ^2 ΔJ=2m1i=1∑m(hθi−y)2
因此,我们的目的就是使得 Δ h \Delta h Δh最小。而 Δ J \Delta J ΔJ又是关于 θ 0 和 θ 1 \theta_0和\theta_1 θ0和θ1的函数。且
h θ i ( x ) = θ 0 + θ 1 x i h_\theta i(x) = \theta_0 + \theta_1x_i hθi(x)=θ0+θ1xi
故定义代价函数的一种,平方误差代价函数为:
J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( ( θ 0 + θ 1 x i ) − y i ) 2 J(\theta_0,\theta_1) = \frac{1}{2m}\color{black} \sum_ {i=1}^m((\theta_0 + \theta_1x_i) - y_i) ^2 J(θ0,θ1)=2m1i=1∑m((θ0+θ1xi)−yi)2
近似处理——仅考虑斜率
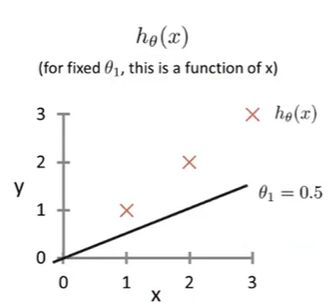
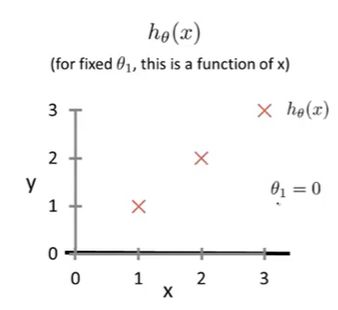
我们先抛开截距不谈,仅仅只考虑斜率。即令 θ 0 = 0 \theta_0 = 0 θ0=0, 观察 θ 1 \theta_1 θ1的变化带来的影响。下图表示了 θ 1 \theta_1 θ1分别取1,0.5,0时的情况:
平方误差代价函数具体值计算过程省略,这里展示J和 θ 1 \theta_1 θ1的关系:

更多的J和 θ 1 \theta_1 θ1的关系如下图所示:

加入截距的考虑
与近似处理不一样,现在我们来研究一个完整的假设函数,即 y = k x + b y = kx + b y=kx+b。这里斜率仍为 θ 1 \theta_1 θ1,截距为 θ 0 \theta_0 θ0。我们的目的仍然是最小化平方误差代价函数。
由于现在的 J ( θ 1 , θ 0 ) J(\theta_1,\theta_0) J(θ1,θ0)是具有两个自变量的函数,因此,此时的 J ( θ 1 , θ 0 ) J(\theta_1,\theta_0) J(θ1,θ0)的函数图像有两个横轴,且图像整体为三维图像:

由于角度问题不好观察到函数最低点,因此我们选择使用等高图(contour plots),以投影的形式展现不同的 θ 1 \theta_1 θ1和 θ 0 \theta_0 θ0所对应的函数值: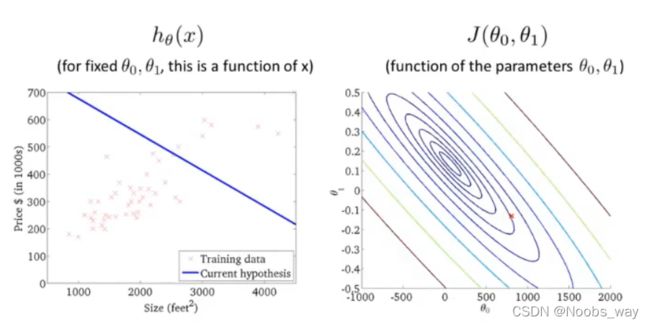
左图即为所取的假设函数与样本数据,右图各个椭圆上的点具有相同的J值, x 处为左图的假设函数的J值表示。
梯度下降
梯度下降的思想
实际上,梯度下降的方法可以从 θ 1 \theta_1 θ1, θ 2 \theta_2 θ2, θ 3 \theta_3 θ3一直扩充到 θ n \theta_n θn的n维,但为了方便起见,这里我们仍然只研究 θ 1 \theta_1 θ1和 θ 0 \theta_0 θ0。
- 选取 θ 1 \theta_1 θ1和 θ 0 \theta_0 θ0的初值,一般从0,0开始。
- 通过不断改变 θ 1 \theta_1 θ1和 θ 0 \theta_0 θ0的值以最快降低J,最终找到一个最小值点。该点的自变量坐标即为我们所要的最终参数。
如图所示,从“山巅”某处出发,算法不断寻找最快“下山“的路径,直到找不到比所在处更低的点为止,即收敛于局部最低点:

梯度下降的算法实现
根据上面的指导思想,我们得出这两个赋值式子:
θ 0 : = θ 0 − α ∂ J ( θ 0 , θ 1 ) ∂ θ 0 \theta_0 := \theta_0 - \alpha \frac{\partial J(\theta_0,\theta_1)}{\partial \theta_0} θ0:=θ0−α∂θ0∂J(θ0,θ1)
θ 1 : = θ 1 − α ∂ J ( θ 0 , θ 1 ) ∂ θ 1 \theta_1 := \theta_1 - \alpha \frac{\partial J(\theta_0,\theta_1)}{\partial \theta_1} θ1:=θ1−α∂θ1∂J(θ0,θ1)
这里的 α \alpha α代表”下山“时步子迈的多大,称为学习率(learing rate)。学习率越大,代表下山的步子迈的越大,反之则越小。
同步更新
这里有一个细节要注意, θ 1 \theta_1 θ1和 θ 0 \theta_0 θ0应该做到同步更新,如下图所示:

原因在于,如果按右图方式计算,那么第三部中的 J ( θ 0 , θ 1 ) J(\theta_0,\theta_1) J(θ0,θ1)中的 θ 0 \theta_0 θ0就和初始的值不一样了,从而导致 θ 1 \theta_1 θ1的变化也受到影响。而左图同步更新的方式更为自然(吴恩达原话)。
导数项的具体阐述
- ∂ J ( θ 0 , θ 1 ) ∂ θ n \frac{\partial J(\theta_0,\theta_1)}{\partial \theta_n} ∂θn∂J(θ0,θ1)
这个问题我们不妨以单变量函数( θ 1 \theta_1 θ1为变量)来阐释,我们的目的是为了根据J值来调整 θ 1 \theta_1 θ1。
假若起点所在处斜率为正,如下图所示:
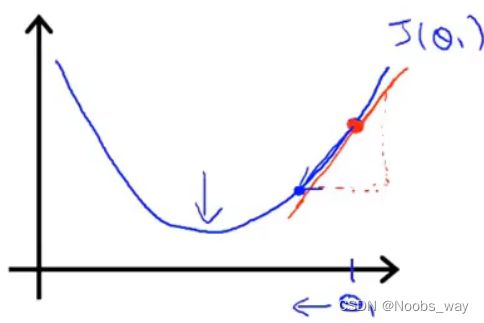
那么 d J ( θ 1 ) ∂ θ 1 \frac{d J(\theta_1)}{\partial \theta_1} ∂θ1dJ(θ1)即为正值,故 新 θ 1 = ( 原 θ 1 − α ∂ J ( θ 0 , θ 1 ) ∂ θ 1 ) < 原 θ 1 新\theta_1=(原 \theta_1 - \alpha \frac{\partial J(\theta_0,\theta_1)}{\partial \theta_1})<原\theta_1 新θ1=(原θ1−α∂θ1∂J(θ0,θ1))<原θ1,这导致 θ 1 \theta_1 θ1向左移动,即最低点移动。
假若起点所在处斜率为负,如下图所示:
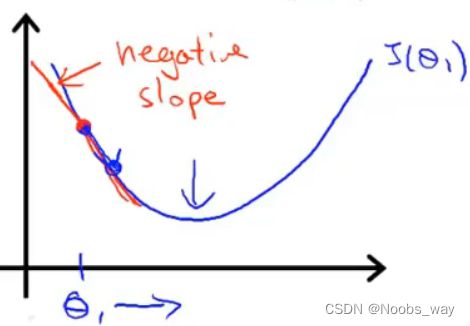
那么 d J ( θ 1 ) ∂ θ 1 \frac{d J(\theta_1)}{\partial \theta_1} ∂θ1dJ(θ1)即为负值,故 新 θ 1 = ( 原 θ 1 − α ∂ J ( θ 0 , θ 1 ) ∂ θ 1 ) > 原 θ 1 新\theta_1=(原 \theta_1 - \alpha \frac{\partial J(\theta_0,\theta_1)}{\partial \theta_1})>原\theta_1 新θ1=(原θ1−α∂θ1∂J(θ0,θ1))>原θ1,这导致 θ 1 \theta_1 θ1向右移动,即最低点移动。
- 学习率 α \alpha α (learing_rate):
先摆出式子:
θ 1 : = θ 1 − α ∂ J ( θ 0 , θ 1 ) ∂ θ 1 \theta_1 := \theta_1 - \alpha \frac{\partial J(\theta_0,\theta_1)}{\partial \theta_1} θ1:=θ1−α∂θ1∂J(θ0,θ1)
当 α \alpha α较小时,迈的步子就会很小,会出现这种情况:
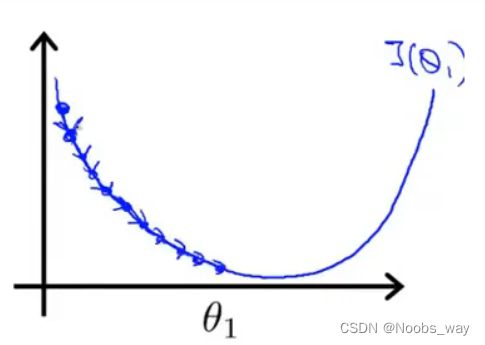
由于每一步迈的很小,导致我们需要很多步才能最终到达最低点,梯度下降将会很慢
当 α \alpha α较大时,迈的步子就会很大,会出现这种情况:
由于步子迈的过大,我们会一次次越过最低点,最终将导致难以收敛甚至发散。
事实上,理想的梯度下降过程,是即使我们保持 α \alpha α不变,点最终也会趋于最低点。如下图所示,当我们每走一步时,所到的新地方一定是越来越平缓的,这就导致了 α ∗ ∂ J ( θ 0 , θ 1 ) ∂ θ 0 \alpha*\frac{\partial J(\theta_0,\theta_1)}{\partial \theta_0} α∗∂θ0∂J(θ0,θ1)越来越小,直至到最低点时斜率为0导致乘积为0,点不会移动。
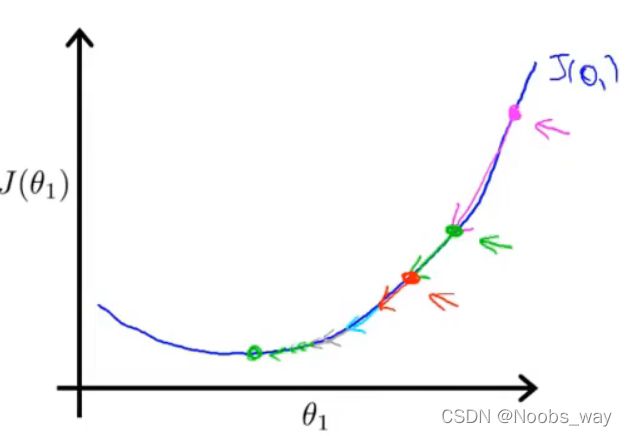
同时,我们在下面给出 ∂ J ( θ 0 , θ 1 ) ∂ θ 1 \frac{\partial J(\theta_0,\theta_1)}{\partial \theta_1} ∂θ1∂J(θ0,θ1)和 ∂ J ( θ 0 , θ 1 ) ∂ θ 0 \frac{\partial J(\theta_0,\theta_1)}{\partial \theta_0} ∂θ0∂J(θ0,θ1)的具体表达式:
由于 J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( ( θ 0 + θ 1 x i ) − y i ) 2 J(\theta_0,\theta_1) = \frac{1}{2m}\color{black} \sum_ {i=1}^m((\theta_0 + \theta_1x_i) - y_i) ^2 J(θ0,θ1)=2m1i=1∑m((θ0+θ1xi)−yi)2
因此 ∂ J ( θ 0 , θ 1 ) ∂ θ 1 = 1 m ∑ i = 1 m ( ( θ 0 + θ 1 x i ) − y i ) ∗ x i \frac{\partial J(\theta_0,\theta_1)}{\partial \theta_1}= \frac{1}{m}\sum_ {i=1}^m((\theta_0 + \theta_1x_i) - y_i)*x_i ∂θ1∂J(θ0,θ1)=m1i=1∑m((θ0+θ1xi)−yi)∗xi
∂ J ( θ 0 , θ 1 ) ∂ θ 0 = 1 m ∑ i = 1 m ( ( θ 0 + θ 1 x i ) − y i ) \frac{\partial J(\theta_0,\theta_1)}{\partial \theta_0}= \frac{1}{m}\sum_ {i=1}^m((\theta_0 + \theta_1x_i) - y_i) ∂θ0∂J(θ0,θ1)=m1i=1∑m((θ0+θ1xi)−yi)
故
θ 1 : = θ 1 − α 1 m ∑ i = 1 m ( ( θ 0 + θ 1 x i ) − y i ) ∗ x i \theta_1 := \theta_1 - \alpha\frac{1}{m}\sum_ {i=1}^m((\theta_0 + \theta_1x_i) - y_i)*x_i θ1:=θ1−αm1i=1∑m((θ0+θ1xi)−yi)∗xi
θ 0 : = θ 0 − α 1 m ∑ i = 1 m ( ( θ 0 + θ 1 x i ) − y i ) \theta_0 := \theta_0 - \alpha\frac{1}{m}\sum_ {i=1}^m((\theta_0 + \theta_1x_i) - y_i) θ0:=θ0−αm1i=1∑m((θ0+θ1xi)−yi)