分支限界法求解迷宫问题

问题描述

从入口出发，按某一方向向前探索，若能走通(未走过的），即某处可以到达，则到达新点，否则试探下一方向；若该点所有的方向均没有通路，则沿原路返回到前一点，换下一个方向再继续试探，直到所有可能的通路都探索到，或找到一条通路，或无路可走又退回到入口点。
退回到的“前一点”正是刚刚才被访问过的，具有“后进先出”的特性，需要用栈保存所能够到达的每一点的下标及从该点前进的方向。

迷宫问题数据结构

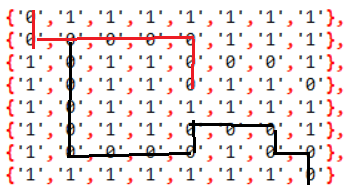
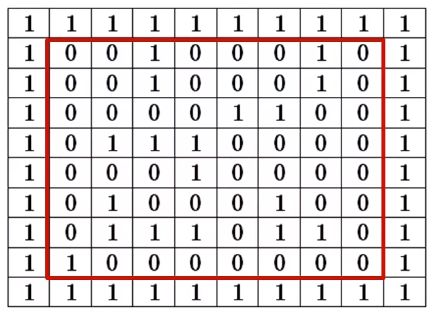
用二维数组maze[M][N]来表示迷宫，图中红框内的部分为迷宫，而迷宫的四周的值全部为1(即不通）。这样设计的话，将迷宫中所有点都演变成迷宫中部的某点，可以保证无论哪个点的试探方向都是4个。

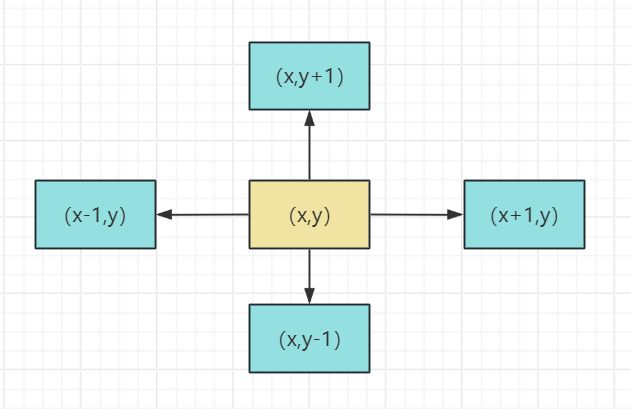
方向试探表示

typedef struct{
	//x,y方向的向量
	int incX,intcY; 
} Direction;
Direction direct[4];
//从某点（x，y）按某一方向v（0<=v<=3）达到新的点（line，col）的坐标
line=x+direct[v].incX;
col=y+direct[v].intcY;

栈中元素的组织

typedef struct{
	int x,y;//当前访问的迷宫格子的横纵坐标 
	int direction;//当前方向 
}Box; 

防止重复到达某点

方案一：

• 另外设置标志数组flag[m][n],其所有元素初始化为0，当达到某一点（i，j）时，将其对应的flag[i][j]设置为1，下次试探到该位置时，就不能选它了。
  方案二

• 当到达某点（i，j）后将对应maze[i][j]设置为-1，其它点未到达过的点其值只能是1或0，可与未到达过的点区别开

代码实现

#include
#define MAXQ 100
#define MAZN 10
//初始化迷宫 
int n=8;
char Maze[MAZN][MAZN]={
	{'0','1','1','1','1','1','1','1'},
	{'0','0','0','0','0','1','1','1'},
	{'1','0','1','1','0','0','0','1'},
	{'1','0','1','1','0','1','1','0'},
	{'1','0','1','1','1','1','1','1'},
	{'1','0','1','1','0','0','0','1'},
	{'1','0','0','0','0','1','0','0'},
	{'1','1','1','1','1','1','1','0'}
};
	//方向结构体 
	struct Direction{
		int incX,incY;
	};
	 Direction dir[4]={{0,-1},{1,0},{0,1},{-1,0}}; 
	//当前位置,探索的方向 
	struct Position{
		int x,y;
		int pre;
	};
	Position qu[MAXQ];
	//队头和队尾 
	int front=-1,rear=-1;
	//输出迷宫路径 
	void disppath(int front)
	{
		int i,j;
		//之前走过设置为-1的都还原为0 
		for(i=0;i<n;i++)
			for(j=0;j<n;j++)
				if(Maze[i][j]=='-1')
					Maze[i][j]='0';
		int k=front;
		//能走通的路径设置为空 
		while(k!=-1)
		{
			Maze[qu[k].x][qu[k].y]=' ';
			k=qu[k].pre;
		}
		//遍历出该路径 
		for(i=0;i<n;i++)
		{
			printf(" ");
			for(int j=0;j<n;j++)
				printf("%c",Maze[i][j]);
			printf("\n");
		}
		//输出路径具体位置
		for(i=0;i<n;i++)
		{
			for(int j=0;j<n;j++)
			if(Maze[i][j]==' ')
			printf("(%d,%d)-->",i,j); 
		 } 
		 printf("End");
	}
	//广度优先遍历 
	void BFS(int x,int y)
	{
		Position p,p1,p2;
		p.x=x;p.y=y;p.pre=-1;
		//走过的位置为-1，下次不能再走了 
		Maze[p.x][p.y]='-1';
		//队尾++ 
		rear++;
		//更新当前解 
		qu[rear]=p;
		while(front!=rear)
		{
			//队头++ 
			front++;
			p1=qu[front];
			//找到一条通路，输出路径 
			if(p1.x==n-1&&p1.y==n-1)
			{
				disppath(front);
				return;
			}
			//试探上，右，下，左四个方向（0，-1）（1,0）（0,1）（-1,0） 
			for(int k=0;k<4;k++)
			{
				p2.x=p1.x+dir[k].incX;
				p2.y=p1.y+dir[k].incY;
				//满足，不能为负，不能超出迷宫，要是通路 
				if(p2.x>=0&&p2.y>=0&&p2.x<n&&p2.y<n&&Maze[p2.x][p2.y]=='0')
				{
					//该位置走过为-1 
					Maze[p2.x][p2.y]='-1';
					//更新方向 
					p2.pre=front;
					rear++;
					//入队 
					qu[rear]=p2;
				}
			}
		}
	}
	int main()
	{
		int x=0,y=0;
		printf("迷宫路径：\n");
		BFS(x,y);
		return 0;
	}

迷宫路径：
  1111111
   111111
 1 111111
 1 111110
 1 111111
 1 11   1
 1    1
 1111111
 
(0,0)-->(1,0)-->(1,1)-->(2,1)-->(3,1)-->(4,1)-->(5,1)-->(5,4)-->(5,5)-->(5,6)-->(6,1)-->(6,2)-->(6,3)-->(6,4)-->(6,6)-->(6,7)-->(7,7)-->End