AVLtree（平衡二叉树）

      AVLtree是一个 “加了额外平衡条件” 的二叉搜索树， 相对于二叉树搜索树而言， 在设计的时候可以说是节点信息添加了平衡因子（也就是个int变量）这个概念。

      我们在设计节点信息类的时候，里面的成员变量有左孩子指针、有孩子指针、存储的值（value）， 再添加一个平衡因子(bq， bq是int类型)和父亲指针。

1、为什么添加平衡因子呢？ 并且和二叉搜索树有什么关联呢？
      答：我们都知道二叉搜索树的概念和特性（前提：这块不懂二叉搜索树可以看以前我写的一篇二叉搜索树文章）， 它有一个致命的缺点，就是在构建的时候不正规的插入数据， 会导致树本身的高度n很大，（举例从1到9顺序插入，每个节点只有右孩子无左孩子，就像链表一样）。 而时间效率O(logn)就是跟高度n有关， 因此AVLtree添加平衡因子就是为了解决高度n不合理的问题， 从而提升树一些查找、插入、删除接口的效率。

2、平衡因子
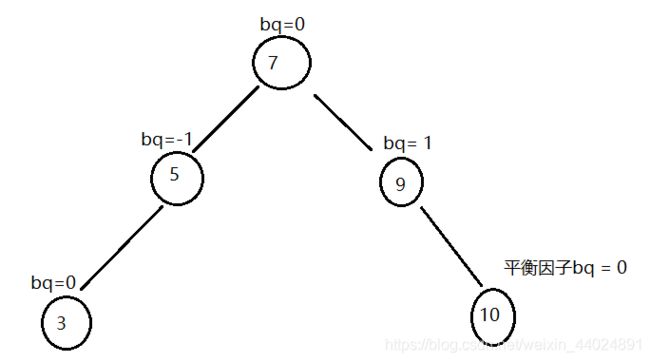
      1、平衡因子的计数方式为 = 该节点右子树的高度 - 该节点左子树的高度
      2、合理的树每个节点平衡因子的取值应为-1、0、1三种，如果出现不同的取值（2、-2），需要进行调整操作（下面说）

AVLtree部分接口实现

a、定义节点信息

//定义AVLtree树节点信息
template<class T>
struct Node {
	
	Node(T val = 0)
		:_value(val)
		,_bq(0)
		,_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
	{

	}

	struct Node<T>* _left;
	struct Node<T>* _right;
	struct Node<T>* _parent;
	T _value;
	int _bq;
};

b、查找接口
      查找和二叉搜索树的方式一样， 这块不做介绍！

	AVLNode Find_Node(const T& value) {
		
		if (!_root) {
			return nullptr;
		}

		AVLNode cur = _root;
		while (cur) {
			//找到了
			if (cur->_value == value)
				return cur;
			//查找的值大于 < cur节点的值，往左边走 
			if (cur->_value > value)
				cur = cur->_left;
			else	//往右边走
				cur = cur->_right;
		}
		//cur == nullptr, 没有找到
		return nullptr;
	}

c、插入接口
      1、重复， 先找到合适的插入位置，如果发现重复， 和二叉搜索树一样， 不支持值重复， 返回false
      2、不重复， 先找到合适的插入位置， 进行插入、 插入完毕之后需要更新平衡因子（更新平衡因子下面重点讲）。
      3、 树为空， 插入完毕之后， 更新头节点。

      以上第二种情况插入没什么说的， 关键在于更新平衡因子，而更新平衡因子答题可以分为3类

1> 第一种情况
      满足条件： parent->bq由(-1->0) 或 (1->0)

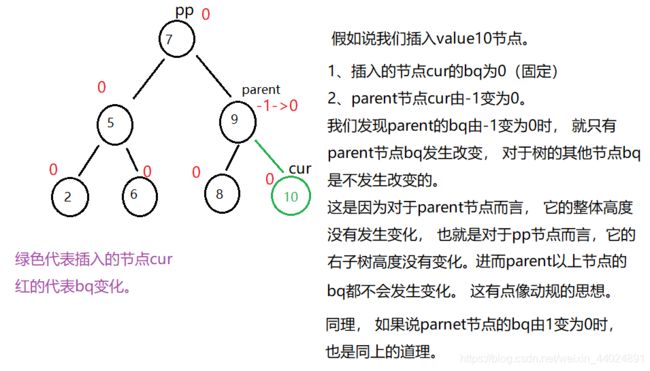
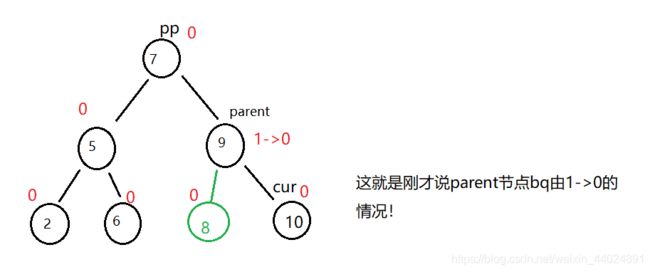
      满足条件：parent->bq从（0->1）或 (0->-1)

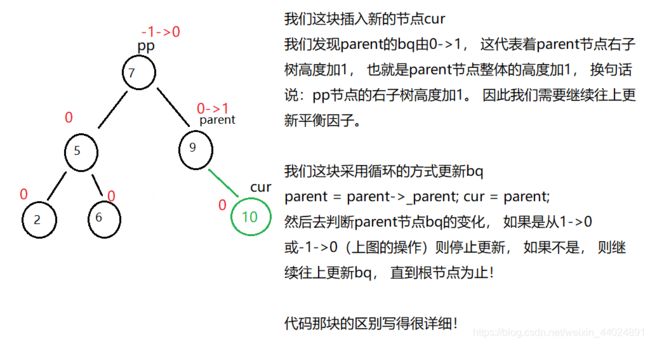
2> 第二种情况

a、左旋一次
      满足左旋的条件为：parent->_bq == 2 并且 cur->_bq == 1;
      而且左旋完毕之后一定会满足parent->_bq == 0, cur->_bq == 0, 这是固定的， 左旋完成之后是不需要更新往上更新的！

      ps: 如果parent节点是头节点， 左旋完成之后需要更新头节点信息。 这个简单，重点在于旋转。(所以请参考代码)


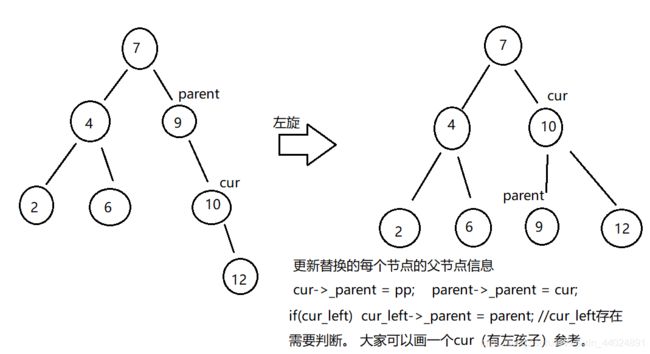
      对比未插入节点， 插入后左旋后， 整体的高度不会发生改变， 大家可以看图得出。

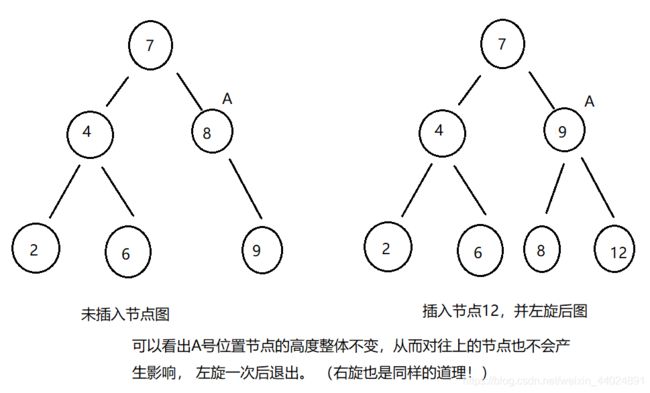
b、右旋一次
      右旋的条件： parent->_bq == -2 并且 cur->_bq == -1;
      右旋只是操作改变， 特性和特点和左旋一样。 这块不做重点， 参考左旋理解。 右旋之后parent->_bq == cur->_bq == 0;
      右旋之后也会满足parent->_bq == cur->_bq == 0, 停止往上更新。

      ps: 如果parent节点是头节点， 右旋完成之后需要更新头节点信息。 这个简单，重点在于旋转。(所以请参考代码)

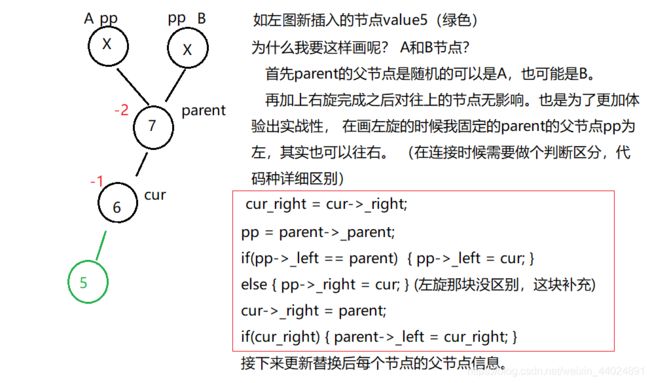
3>第三种情况
      第三种情况为双旋， 分为左右双旋和右左双旋*。
      1、左右双旋（先左旋后右旋）。 条件： parent->bq == 2 并且 cur->_bq == -1
      1、右左双旋（先右旋后左旋）。 条件： parent->bq == -2 并且 cur->_bq == 1

      如果parent节点是头节点， 双旋完成之后需要更新头节点信息。 这个简单，重点在于旋转。(所以请参考代码)

a、先看右左双旋

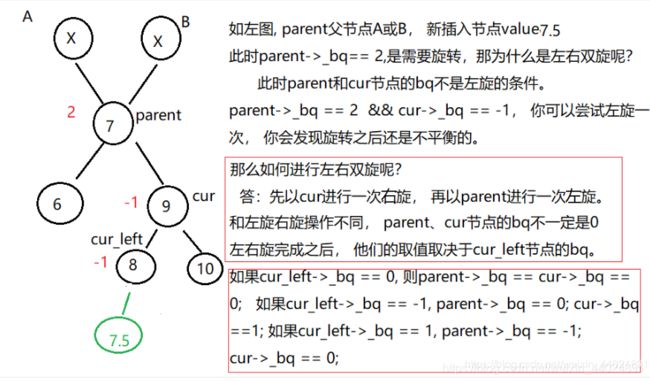
      if(cur_left->_bq == -1)

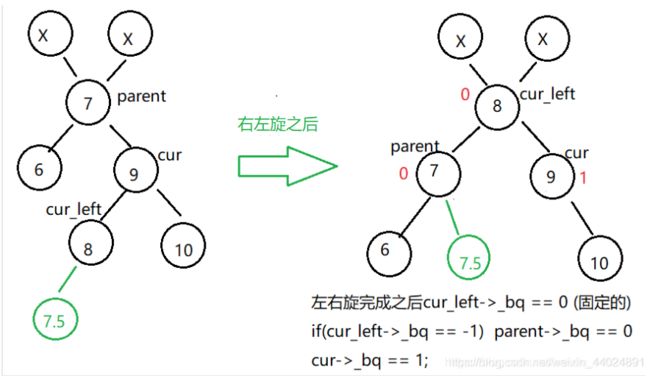
      if(cur_left->_bq == 1)

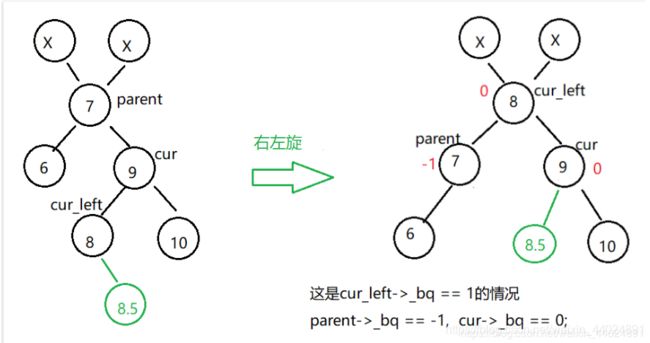
b、左右双旋
      左右双旋： 先以cur左旋， 再以parent右旋。 旋转之后parent、cur节点的bq值大家可以手动画一下得出结论。我就不再画图解释。

下面画好之后parent、cur结点的变化：
      if(cur_right->_bq == -1), parent->_bq == 1;cur->_bq == 0;
      if(cur_right->_bq == 1), parent->_bq == 0;cur->_bq == -1;

ps: 我喜欢用 ‘==’ 符号代表等于， ‘=’ 代表赋值， 在文本中写也是的。

以上就是插入接口的全部分类！

//左旋操作函数
void Rotate_Left(AVLNode& parent) {
		
		AVLNode SubR = parent->_right;
		AVLNode SubRL = SubR->_left;

		SubR->_left = parent;
		parent->_right = SubRL;

		AVLNode pp = parent->_parent;

		if (pp) {	//parent不是头节点
			if (pp->_left = parent)
				pp->_left = SubR;
			else
				pp->_right = SubR;
		}
		else {		//parent是头节点
			
			_root = SubR;
		}

		SubR->_parent = pp;
		if(SubRL)
			SubRL->_parent = parent;
		parent->_parent = SubR;

		SubR->_bq = parent->_bq = 0;
	}

//右旋操作函数
void Rotate_Right(AVLNode& parent) {

		AVLNode SubL = parent->_left;
		AVLNode SubLR = SubL->_right;

		SubL->_right = parent;
		parent->_left = SubLR;
		
		AVLNode pp = parent->_parent;

		if (pp) {		//parent不是头节点
			if (pp->_left = parent)
				pp->_left = SubL;
			else
				pp->_right = SubL;
		}
		else {			//parent是头节点
			_root = SubL;
		}

		SubL->_parent = pp;
		if(SubLR)
			SubLR->_parent = parent;
		parent->_parent = SubL;

		SubL->_bq = parent->_bq = 0;
	}

//插入接口
bool Insert_Node(const T& value) {
		
		if (!_root) {
			_root = new AVNode(value);
			return true;
		}

		AVLNode cur = _root;
		AVLNode parent = nullptr;

		while (cur) {
			parent = cur;
			if (cur->_value == value)
				return false;
			if (cur->_value > value)
				cur = cur->_left;
			else
				cur = cur->_right;
		}

		cur = new AVNode(value);	//创建一个节点

		if (parent->_value > value)
			parent->_left = cur;
		else
			parent->_right = cur;
		cur->_parent = parent;

		//更新平衡因子
		while (parent) {

			if (parent->_left == cur)
				parent->_bq--;
			else
				parent->_bq++;

			if (parent->_bq == 0)
				break;

			else if (abs(parent->_bq) == 1) {
				cur = parent;
				parent = parent->_parent;		
			}

			else if ((parent->_bq == 2) && (cur->_bq == 1)) {
				//单旋 - 左旋操作
				Rotate_Left(parent);
				break;
			}
			else if ( (parent->_bq == -2) && (cur->_bq == -1) ) {
				//单旋 - 右旋操作
				Rotate_Right(parent);
				break;
			}
			else if ( (parent->_bq == 2) && (cur->_bq == -1) ) {
				//左右双旋
				
				AVLNode SubR = cur;
				AVLNode SubRL = SubR->_left;
				int bq = SubRL->_bq;

				Rotate_Left(cur);
				Rotate_Right(parent);
	
				if (-1 == bq) {
					parent->_bq = 0;
					SubR->_bq = 1;
				}
				else if (1 == bq) {
					parent->_bq = -1;
					SubR->_bq = 0;
				}

				break;
			}	
			else if ( (parent->_bq == -2) && (cur->_bq == 1)) {
				//右左双旋

				AVLNode SubL = cur;
				AVLNode SubLR = cur->_right;
				int bq = SubLR->_bq;

				Rotate_Right(cur);
				Rotate_Left(parent);

				if (-1 == bq) {
					parent->_bq = 1;
					SubL->_bq = 0;
				}
				else if (1 == bq) {
					parent->_bq = 0;
					SubL->_bq = -1;
				}

				break;
			}
			else {
				return false;
			}
		}
		
		return true;
	}

d、求节点深度n接口

	int Tree_Depth(const AVLNode& root) {
		if (!root) {
			return 0;
		}

		int left = Tree_Depth(root->_left);
		int right = Tree_Depth(root->_right);

		return left > right ? left + 1 : right + 1;
	}

e、遍历接口
      和二叉搜索树一样，采用中序遍历就可得到有序数列。

	void _Inorder(const AVLNode& root) {
		if (!_root)
			return;

		_Inorder(root->_left);
		cout << root->_value << " ";
		_Inorder(root->_right);
	}

      以上就是AVLtree接口的信息， 当然还有个删除接口，大家可以自己去写， 删除一个节点需要考虑一些信息（是否对往上的节点的平衡因子产生影响？ 什么条件会产生影响？ 产生了影响又该如何处理？） 大家可以思考一下， 借鉴插入接口思考。 总结而言：AVLtree算法的难度在于插入、删除后更新平衡因子。

      相对于二叉搜索树而言， 我们可以显著的发现它的优化和效率提升很好。 对于不正规的插入数据也可以保证很高效率。

就是这些！