2021斯坦福CS224N课程笔记~3
3. 神经网络学习:手工计算梯度
Lecture 3: Neural net learning: Gradients by hand (matrix calculus)
and algorithmically (the backpropagation algorithm)
参考文档:
https://zhuanlan.zhihu.com/p/527211871
https://zhuanlan.zhihu.com/p/414293072
https://looperxx.github.io/CS224n-2019-03-Word%20Window%20Classification,Neural%20Networks,%20and%20Matrix%20Calculus/#11-a-neuron
https://showmeai.tech/article-detail/234
3.1.1. 命名实体识别(NER)
NER 任务:在文本中查找和分类名称(时间-DATA、地点-LOC、人物-PER、组织-ORG),例如:
-
可能的用途
-
- 跟踪文档中提到的特定实体(组织、个人、地点、歌曲名、电影名等)
- 对于问题回答,答案通常是命名实体
- 许多需要的信息实际上是命名实体之间的关联
- 同样的技术可以扩展到其他 slot-filling 槽填充分类
-
通常后面是命名实体链接/规范化到知识库
3.1.1. 1 spaCy文档
一个被命名的实体是一个“现实世界的对象”,它被赋予一个名字——例如,一个人,一个国家,一个产品或者一个书名。spaCy可以通过询问模型来识别文档中的各种类型的命名实体。因为模型是统计的,并且非常依赖于他们所接受的示例,所以这并不总是完美的,并且可能需要稍后进行一些调整,这取决于您的用例。
命名实体可以doc的ents中获取
doc = nlp(u'Apple is looking at buying U.K. startup for $1 billion')
for ent in doc.ents:
print(ent.text, ent.start_char, ent.end_char, ent.label_)
3.1.2. 句子中的命名实体识别
3.1.3. NER的难点
-
很难计算出实体的边界
-
- 第一个实体是 “First National Bank” 还是 “National Bank”
-
很难知道某物是否是一个实体
-
- 是一所名为“Future School” 的学校,还是这是一所未来的学校?
-
很难知道未知/新奇实体的类别
-
- “Zig Ziglar” ? 一个人
-
实体类是模糊的,依赖于上下文
-
- 这里的“Charles Schwab” 是 PER 不是 ORG
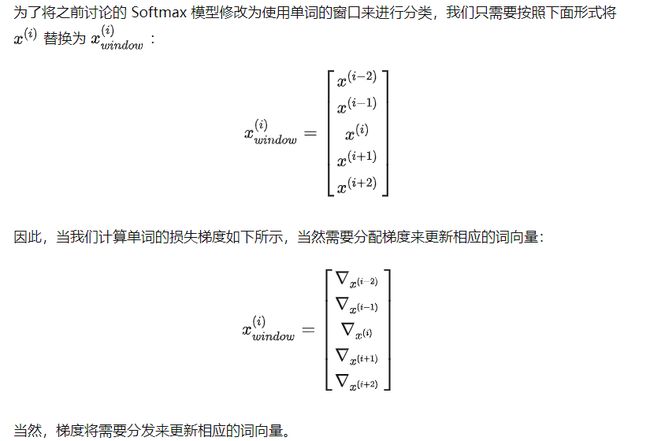
3.1.4. 基于窗口数据的分类预测
3.1.4.1 词-窗分类
-
思路:为在上下文中的语言构建分类器
-
- 一般来说,很少对单个单词进行分类
-
例如,上下文中一个单词的命名实体分类
-
- 人、地点、组织、没有
-
在上下文中对单词进行分类的一个简单方法,可能是对窗口中的单词向量进行平均,并对平均向量进行分类
-
- 问题:这会丢失位置信息
-
简单的 NER 通常使用二元逻辑分类器做窗口分类。
-
主要想法:在相邻词的上下文窗口中对每个词进行分类。
-
主要做法:在手工标记的数据上训练逻辑分类器,以便对每个类别的中心词{yes/no}进行分类(基于窗口中词向量的拼接)。
-
实际上,我们通常使用多类 softmax,但尽量保持简单。
-
示例:在**窗口长度为 2** 的句子上下文中,将“Paris”分类为 +/- 地点(LOC):
结果向量 xwindow = x ∈ R5d ,是一个列向量!然后我们会将这个向量提供给一个分类器,分类器最终就会有一个位置的概率【见3.1.5(2)】。
目前为止,我们主要探讨了使用单个单词向量 x 预测的外部评估任务。在现实中,因为自然语言处理的性质,这几乎不会有这样的任务。在自然语言处理中,常常存在着一词多义的情况,我们一般要利用词的上下文来判断其不同的意义。例如,如果你要某人解释“to sanction”是什么意思,你会马上意识到根据“to sanction”的上下文其意思可能是“to permit”或者“to punish”。在更多的情况下,我们使用一个单词序列作为模型的输入。这个序列是由中心词向量和上下文词向量组成。上下文中的单词数量也被称为上下文窗口大小,并根据解决的问题而变化。一般来说,较窄的窗口大小会导致在句法测试中更好的性能,而更宽的窗口会导致在语义测试中更好的性能。
对所有单词进行分类:在以句子中每个单词为中心的向量上,为每个类别运行分类器
3.1.4.2 最简单的窗口分类器:Softmax
3.1.5. NER:中心词作为地点的二元分类
(1)多层感知器
-
假设我们要对中心词是否为一个地点,进行分类
-
与word2vec类似,我们将遍历语料库中的所有位置。但这一次,它将**受到监督,只有一些位置能够得到高分**。
-
- 例如,在他们的中心有一个实际的NER Location的位置是“真实的”位置会获得高分
(2)神经网络前馈计算
3.1.6. 本章计划
我们将介绍两种方法:
(1) 手工矩阵演算(40 分钟);
(2) 反向传播算法(35 分钟)。
3.2.手工矩阵演算
本节的主要目的是手工计算梯度,通过矩阵演算,得到完全矢量化的梯度。
首先,要认识到“如果你使用矩阵,多变量微积分就像单变量微积分”这个观念的重要性。矩阵计算比非矢量化梯度更快、更有用,但是做一个非矢量化的梯度可以有利于直觉(回忆第一章)。
然后,您要多学习讲义和矩阵演算笔记,其中有详细的介绍资料。您还可以复习 Math 51,它有一本新的在线教科书:http://web.stanford.edu/class/math51/textbook.html;或者,如果您做了 Engr108,那么您可能会更幸运。
3.2.1. 梯度
在向量微积分中,标量场的梯度是一个向量场。标量场中某一点上的梯度指向标量场增长最快的方向,梯度的长度是这个最大的变化率。
在单变量的实值函数的情况,梯度只是导数;或者,对于一个线性函数,梯度就是线的斜率。
3.2.2. 雅可比矩阵
严格地说,梯度是雅可比(Jacobian)矩阵的一个特例。因此,可以从梯度推广到雅可比矩阵。
在向量微积分中,雅可比矩阵是一阶偏导数以一定方式排列成的矩阵,其行列式称为雅可比行列式。
雅可比矩阵的重要性在于它体现了一个可微方程与给出点的最优线性逼近。因此,雅可比矩阵类似于多元函数的导数。
3.2.3. 链式法则
链式法则是微积分中的求导法则,用以求一个复合函数的导数。所谓的复合函数,是指以一个函数作为另一个函数的自变量。
链式法则用文字描述:由两个函数凑起来的复合函数,其导数等于里边函数代入外边函数的值之导数,乘以里边函数的导数。
链式法则用数学描述:若 f(x)=3x,g(x)=x+3,则 g(f(x))就是一个复合函数,并且 g′(f(x))=3;若 h(x)=f(g(x)),则 h’(x)=f’(g(x))g’(x)。
3.2.3.1. 计算b对s的偏导
回到我们的神经网络(见例 3.1 ) , 让我们来求解 ∂ s ∂ b 回到我们的神经网络(见例 3.1),让我们来求解\frac{\partial s}{\partial b} 回到我们的神经网络(见例3.1),让我们来求解∂b∂s
实际上,我们关心的是损失 Jt的梯度。但为了简单起见,我们将计算分数 s 的梯度。
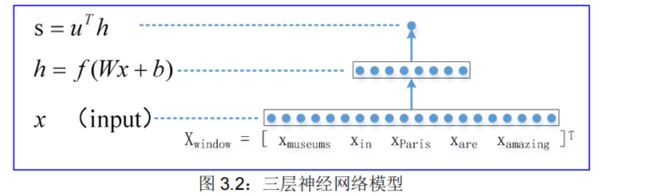
我们把图 3.1 的第四层去掉,变成三层神经网络模型,见图 3.2:
将方程h=f(Wx+b)分解为简单的两个部分h=f(z)和z=Wx+b,最终形成如下方程组:
3.2.3.2. 计算w对s的偏导
假设我们现在要计算 ∂ s ∂ w ,再次使用链式法则,则可得: 假设我们现在要计算\frac{\partial s}{\partial w},再次使用链式法则,则可得: 假设我们现在要计算∂w∂s,再次使用链式法则,则可得:
3.2.3.3. 关于矩阵的导数:输出形状
方程 3.23 右边是转置矩阵相乘的原因是:为了在矩阵运算时保持矩阵维度的匹配!(详见3.2.3.5)
3.2.3.4. 在反向传播中推导本地输入梯度
3.2.3.5. 为什么是转置矩阵?
3.2.3.6. 导数应该是什么形状?
3.3.反向传播算法
我们几乎已经向您展示了反向传播,它采用导数并使用(广义、多元或矩阵)链式法则。
还展示了其他技巧:我们在计算较低层的导数时重用为较高层计算的导数以最小化计算。
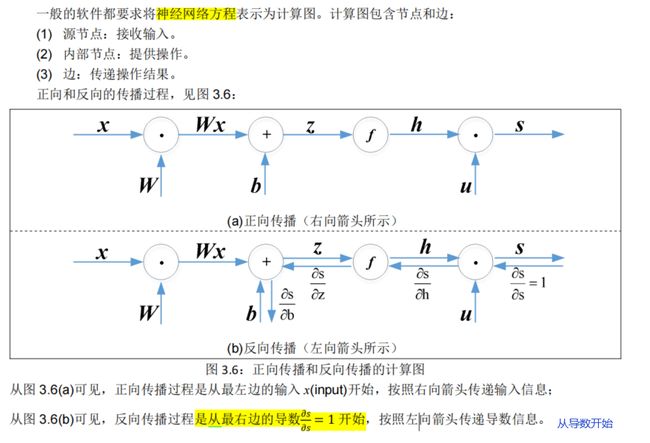
3.3.1. 计算图
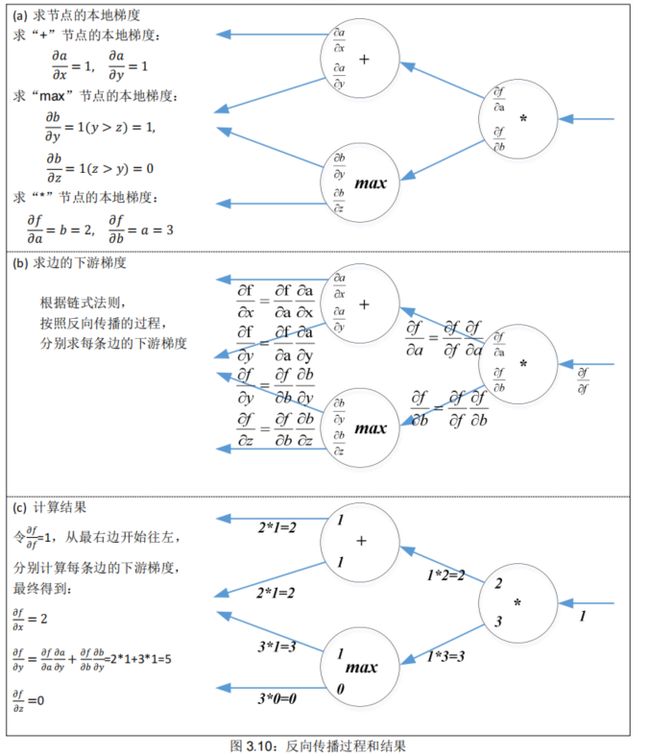
3.3.2. 反向传播:单个节点的表示
在反向传播链上,每个节点接收“上游梯度”,它的目标是传递正确的“下游梯度”。
而且,每个节点都有“本地梯度”,即输出相对于输入的梯度,见图 3.7(a)。
3.3.3. 反向传播:单个节点多输入
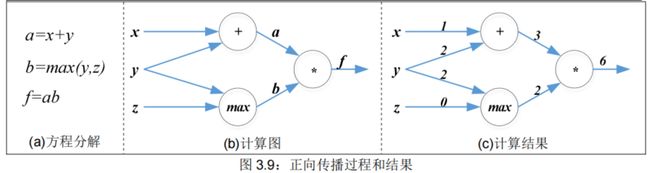
3.3.4. 一个例子
3.3.5. 效率:一次计算所有梯度★
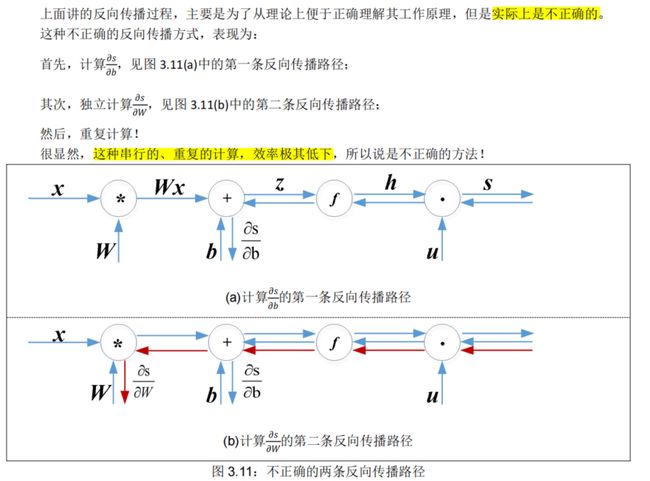
那么,什么是正确的方法呢?
在实际应用中,正确方法是:一次性计算所有梯度(类似我们手动计算梯度时使用的δ,见方程 3.21)。![]()
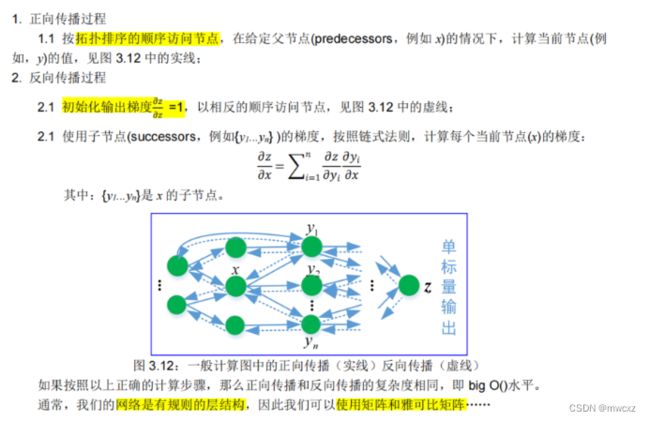
3.3.5.1. 一般计算图中的反向传播
3.3.5.2. 自动微分
本地梯度见:3.3.2. 反向传播:单个节点的表示
3.3.5.3. 正向/反向传播的实现
一般地,实现正向/反向传播的代码,见图 3.14:
特别地,实现正向/反向传播有专用的 API,见图 3.15:
为了计算反向传播,我们需要在前向传播时存储一些变量的值
3.3.6. 手工检查数字梯度
3.4.总结
我们掌握了神经网络的核心技术!
前向传递:计算操作的结果并保存中间值。
反向传播:沿计算图递归地(因此有效地)应用链式法则,即:下游梯度=上游梯度 x 本地梯度。
我们为什么要了解有关梯度的所有这些细节?
因为,虽然现代深度学习框架为您计算梯度(本周五参加 PyTorch 介绍),即编译器或系统为您自动实现正向/反向传播,但是反向传播并不总是完美的;所以,这门课可以使您了解底层工作原理,这对调试和改进模型至关重要。
参见 Karpathy 文章(在教学大纲中):
https://medium.com/@karpathy/yes-you-should-understand-backprop-e2f06eab496b
后续课程中的示例:梯度爆炸和消失。