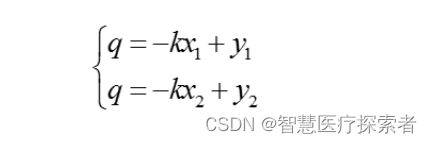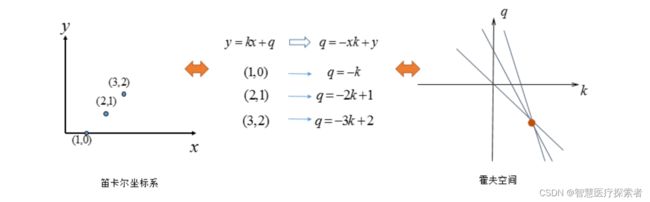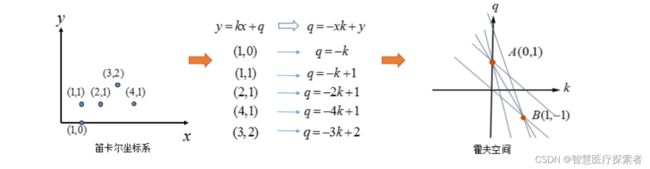计算机视觉：使用opencv进行直线检测

1 直线检测介绍

在图像处理中，直线检测是一种常见的算法，它通常获取n个边缘点的集合，并找到通过这些边缘点的直线。其中用于直线检测，最为流行的检测器是基于霍夫变换的直线检测技术。

1.1 什么是霍夫变换

霍夫变换（Hough Transform）是图像处理中的一种特征提取方法，可以识别图像中的几何形状。它将在参数空间内进行投票来决定其物体形状，通过检测累计结果找到一极大值所对应的解，利用此解即可得到一个符合特定形状的参数。

1.2 霍夫变换原理

一条直线可由两个点A=(X1,Y1)和B=(X2,Y2)确定(笛卡尔坐标)

另一方面，y = kx + q 也可以写成关于（k,q）的函数表达式（霍夫空间）：

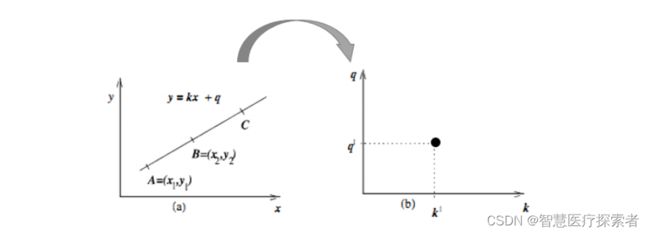
对应的变换可以通过图形直观表示：

变换后的空间成为霍夫空间。即：笛卡尔坐标系中一条直线，对应霍夫空间的一个点。

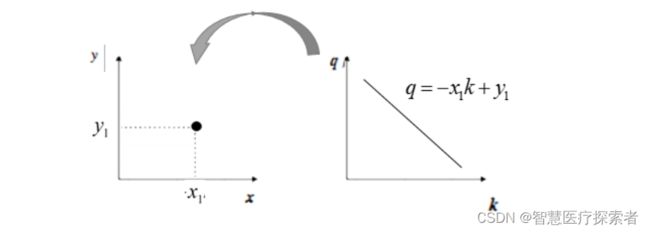
反过来同样成立（霍夫空间的一条直线，对应笛卡尔坐标系的一个点）：

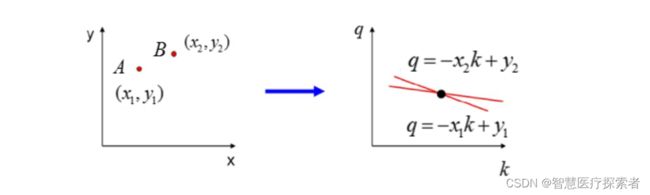
 再来看看A、B两个点，对应霍夫空间的情形：

接下来，再看一下三个点共线的情况： 

 

可以看出如果笛卡尔坐标系的点共线，这些点在霍夫空间对应的直线交于一点：这也是必然，共线只有一种取值可能。

如果不止一条直线呢？再看看多个点的情况（有两条直线）：

其实（3，2）与（4，1）也可以组成直线，只不过它有两个点确定，而图中A、B两点是由三条直线汇成，这也是霍夫变换的后处理的基本方式：选择由尽可能多直线汇成的点。

霍夫空间：选择由三条交汇直线确定的点（中间图），对应的笛卡尔坐标系的直线（右图）。

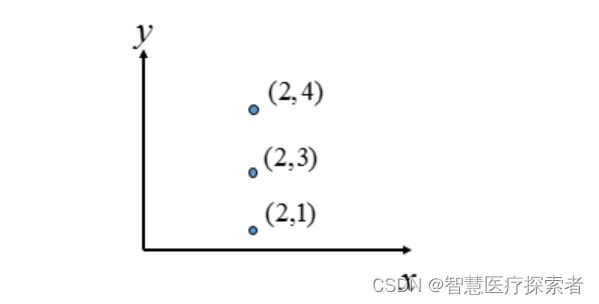
到这里问题似乎解决了，已经完成了霍夫变换的求解，但是如果像下图这种情况呢？

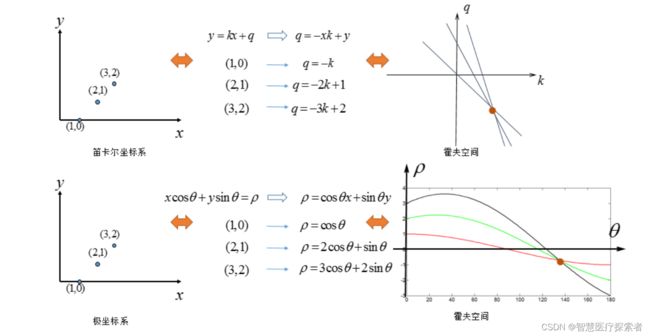
k=∞是不方便表示的，而且q怎么取值呢，这样不是办法。因此考虑将笛卡尔坐标系换为：极坐标表示。

在极坐标系下，其实是一样的：极坐标的点→霍夫空间的直线，只不过霍夫空间不再是[k,q]的参数，而是的参数，给出对比图： 

2 使用opencv进行直线检测

在使用霍夫变换侦测直线前，须先利用边缘检测算法来减少图像的数据量、剔掉不相关的信息，保留图像中重要的结构特征。

2.1 图像灰度化

原始图像与灰度化的图像如下：

2.2 边缘检测

利用边缘检测算法（Canny、Sobel、Laplacian等）来检测物体边缘，代码如下：

canny = cv2.Canny(gray_img, 30, 150)

2.3 霍夫变换

使用霍夫变换来得出直线检测结果，代码如下：

lines = cv2.HoughLines(canny, 1, np.pi / 180, 180)
lines1 = lines[:, 0, :]
for rho, theta in lines1[:]:
    a = np.cos(theta)
    b = np.sin(theta)
    x0 = a * rho
    y0 = b * rho
    x1 = int(x0 + 3000 * (-b))
    y1 = int(y0 + 3000 * (a))
    x2 = int(x0 - 3000 * (-b))
    y2 = int(y0 - 3000 * (a))
    cv2.line(im, (x1, y1), (x2, y2), (0, 0, 255), 2)

运行结果显示如下：

2.4 完整代码

import cv2
import numpy as np


im = cv2.imread("../data/ladder.jpg")

cv2.imshow('original', im)
cv2.waitKey(0)

gray_img = cv2.cvtColor(im, cv2.COLOR_BGR2GRAY)
cv2.imshow('gray', gray_img)
cv2.waitKey(0)

canny = cv2.Canny(gray_img, 30, 150)
cv2.imshow('canny', canny)
cv2.waitKey(0)

lines = cv2.HoughLines(canny, 1, np.pi / 180, 180)
lines1 = lines[:, 0, :]
for rho, theta in lines1[:]:
    a = np.cos(theta)
    b = np.sin(theta)
    x0 = a * rho
    y0 = b * rho
    x1 = int(x0 + 3000 * (-b))
    y1 = int(y0 + 3000 * (a))
    x2 = int(x0 - 3000 * (-b))
    y2 = int(y0 - 3000 * (a))
    cv2.line(im, (x1, y1), (x2, y2), (0, 0, 255), 2)

cv2.imshow('original', im)
cv2.waitKey(0)

3 使用opencv检测倾角

import cv2
import numpy as np
 
def line_detect(image):
  # 将图片转换为HSV
  hsv = cv2.cvtColor(image, cv2.COLOR_BGR2HSV)
  # 设置阈值
  lowera = np.array([0, 0, 221])
  uppera = np.array([180, 30, 255])
  mask1 = cv2.inRange(hsv, lowera, uppera)
  kernel = np.ones((3, 3), np.uint8)
 
  # 对得到的图像进行形态学操作（闭运算和开运算）
  mask = cv2.morphologyEx(mask1, cv2.MORPH_CLOSE, kernel) #闭运算：表示先进行膨胀操作，再进行腐蚀操作
  mask = cv2.morphologyEx(mask, cv2.MORPH_OPEN, kernel)  #开运算：表示的是先进行腐蚀，再进行膨胀操作
 
  # 绘制轮廓
  edges = cv2.Canny(mask, 50, 150, apertureSize=3)
  # 显示图片
  cv2.imshow("edges", edges)
  # 检测白线  这里是设置检测直线的条件，可以去读一读HoughLinesP()函数，然后根据自己的要求设置检测条件
  lines = cv2.HoughLinesP(edges, 1, np.pi / 180, 40,minLineLength=10,maxLineGap=10)
  print "lines=",lines
  print "========================================================"
  i=1
  # 对通过霍夫变换得到的数据进行遍历
  for line in lines:
    # newlines1 = lines[:, 0, :]
    print "line["+str(i-1)+"]=",line
    x1,y1,x2,y2 = line[0]  #两点确定一条直线，这里就是通过遍历得到的两个点的数据 （x1,y1）(x2,y2)
    cv2.line(image,(x1,y1),(x2,y2),(0,0,255),2)   #在原图上画线
    # 转换为浮点数，计算斜率
    x1 = float(x1)
    x2 = float(x2)
    y1 = float(y1)
    y2 = float(y2)
    print "x1=%s,x2=%s,y1=%s,y2=%s" % (x1, x2, y1, y2)
    if x2 - x1 == 0:
      print "直线是竖直的"
      result=90
    elif y2 - y1 == 0 :
      print "直线是水平的"
      result=0
    else:
      # 计算斜率
      k = -(y2 - y1) / (x2 - x1)
      # 求反正切，再将得到的弧度转换为度
      result = np.arctan(k) * 57.29577
      print "直线倾斜角度为：" + str(result) + "度"
    i = i+1
  #   显示最后的成果图
  cv2.imshow("line_detect",image)
  return result
 
if __name__ == '__main__':
  # 读入图片
  src = cv2.imread("lines/line6.jpg")
  # 设置窗口大小
  cv2.namedWindow("input image", cv2.WINDOW_AUTOSIZE)
  # 显示原始图片
  cv2.imshow("input image", src)
  # 调用函数
  line_detect(src)
  cv2.waitKey(0)