机器学习从入门到死亡(上)

机器学习简介

机器学习（machine learning）是人工智能（artificial intelligence）的一个分支。使用算法来生成模型来帮助计算机处理数据，达到预测或回归等目的。原始的程序处理思想是计算机根据数据和程序来计算得到输出。但是机器学习是根据数据和已知的输出或任务来分析得到模型（程序），输入计算机的是data数据和output。也就是人类无需自己计算模型，这一任务将由计算机完成。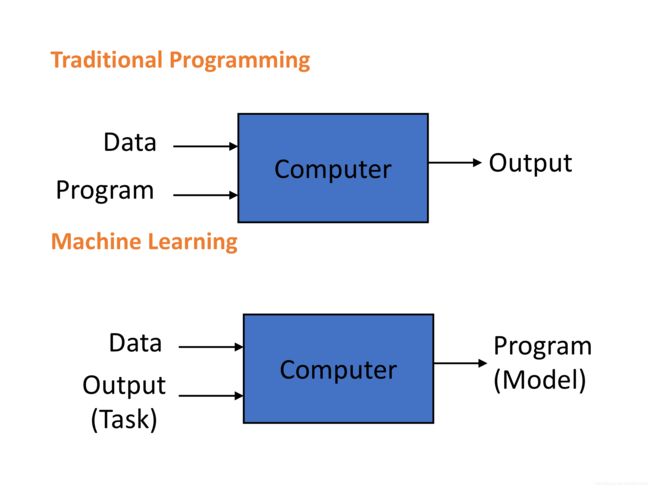
图片来自ANU教材

---

前言

经过在澳洲国立大学两年的机器学习之后，我把所学的机器学习知识汇总成了这篇笔记。从简单的数学知识，到经典统计机器学习算法，再到神经网络均有涉及。

---

一、机器学习的种类

根据输入数据是否需要人为处理可以把机器学习分为有监督学习，无监督学习和半监督学习。数据事先经过人处理可以被打印上标签（label），这一过程可以理解为有人为计算机提供目标值并监督计算机进行模型学习。而对于未经认为处理，即不带有标签的数据，进行的机器学习叫无监督学习。如果输入的数据中部分带有标签，部分没有标签，那么进行的是半监督学习。

1.有监督学习（supervised learning）

对事先带有标签的数据进行机器学习，叫有监督学习。比如对一个班的学生进行分类，有好学生和坏学生。每个学生会有年龄，成绩，出勤率等信息，这些是输入向量。老师对一部分学生已经进行了认为的分类，有的被分为好学生，有的是坏学生，这是打上标签。计算机输入好学生和坏学生的信息，输出一个分类模型，这就是有监督学习。之后可以再用这个模型去预测其他班级的学生是好学生还是坏学生。

有监督学习又分为线性回归（linear regression），非线性回归（non-linear regression），线性分类（linear classification），非线性分类（non-linear classification）。线性回归中常见的有一元线性回归和多元线性回归，非线性回归常见有感知机和神经网络等，线性分类常见有支持向量机（svm），非线性分类有k近邻（knn），决策树和朴素贝叶斯算法。

2.无监督学习（unsupervised learning）

无监督学习处理的是不带有标签的数据，多半是原始数据未经处理。这类数据的特点是数据信息复杂，包含无用信息，但是数据量充足，获取容易。比如还是那个班的学生，但是学生数据没有经过老师事先分类，仅包含采集到的学生基础信息。使用无监督学习训练一个模型，将这个班的学生分成几个内部关系近的小组，比如甲乙丙三人经常一起玩耍就把三人分为一组。这个就是无监督学习中的聚类。

无监督学习可以分成聚类（clustering）和维度下降（dimensionality reduction）。聚类是把数据点分成不同的几个簇，常见的聚类方法有kmeans（k均值）和EM算法。维度下降又可以叫subspace learning，就是提取数据中部分主要信息，比如是把三维数据中提取一个平面（二维）进行分析，常见的方法有PCA（主成分分析）。

无监督学习也可以进行分类，比如使用无标签的数据训练一个三分类的分类器。可以先假设一个三分类器，用它去计算数据的信息总量（the total amount of information）。然后对数据进行聚类分成三类，可以使用kmeans。然后从三类数据中分别选部分数据，计算它们的最小信息总量，把这些数据打上标签对应分类。然后将带有标签的数据带入假设的分类器中进行再训练。这样就可以对原本属于无监督的数据进行分类。当然这种方法的误差可能较大，更常见的是使用一部分有标签的数据再结合大量无标签的数据，一起学习建模。这也就是下面的半监督学习。

3.半监督学习（semi-supervised learning）

当部分数据带有标签，其余数据不带有标签，进行的是半监督学习。半监督学习意义是利用更多数据进行更精准预测和分类。有监督学习所利用的是少量标签数据，建立的模型在边界处理中可能存在不定项和误差。为了利用更多数据，可以使用无监督学习（比如聚类）对数据进行进一步分析得到精准模型。比如下图中，有监督学习生成的分类线在判断点a时，无法给出准确分类，因为a点就在边界上。可是在利用kmeans进行聚类后发现，a点属于B类，而B类大部分点都在分类界线之下。而分类线之上的A类距离a点较远，所以此时可以准确的把a点归于分类线之下。我们也可以在有监督学习之前可以使用无监督学习进行预处理，比如在神经网络之前使用kmeans进行预处理。

下面附上机器学习经典库scikit-learn中的不同机器学习方法分类图。图中根据输入数据的大小和是否带标签以及机器学习的目标，对应使用不同机器学习方法。

---

二、线性代数

1.向量和矩阵

1.1 向量（vectors）

向量又叫矢量，是带有方向的特殊object。向量计算有封闭性，即向量加上或乘以一个标量（scalars）得到的还是一个同类型（同方向）向量。向量可以有n维，即向量属于Rⁿ（包含n个数的元组tuples）。

1.2 矩阵（matrices）

如下图所示，A是一个m*n的矩阵，矩阵A有n行（rows）和m列（columns）。当m或n为1时，矩阵A就简化成了一个向量。

1.3 矩阵的运算

矩阵的加法适用于两个维度一样的矩阵，它们的和是对应位置的数相加。

矩阵的乘法是将矩阵A（R^{m * n}）和矩阵BA（R^{n * k}）相乘得到矩阵CA（R^m*k），其中C的元素为

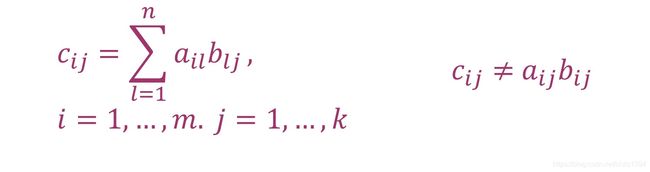
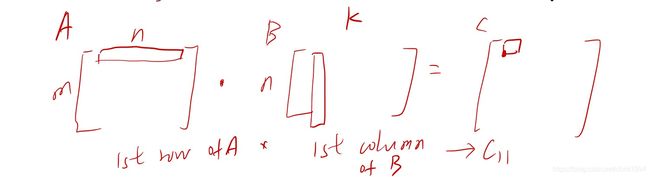
即用A的行乘以B的列得到对应位置的C元素。如图所示：

矩阵的乘法不具有交换律，即A * B不等于B * A。但是矩阵的乘法有结合律和分配律。矩阵乘法结合律（associativity）是(A * B) * C=A * (B * C)，矩阵的分配律（distributivity）是(A+B) * C=A * C+B * C, A * (C+D)=A * C+A * D。

当一个矩阵只有主对角线上有数字且都为1，其余位置均为0时，这个矩阵称为单位矩阵（identity matrix），n维单位矩阵记为I_n。任意矩阵乘以单位矩阵还是它自己，即对于A属于R^m*n，I_m * A=A * I_n=A。

1.4 逆矩阵与矩阵的转置

对于一个方阵A（矩阵A的行数和列数相等），如果另一个方阵B满足A * B=I _n= B * A，那么B就是A的逆矩阵（inverse），也可以记为A^-1。

对于任意一个矩阵A，A∈R^{m * n}，如果矩阵B（B∈R^{n * m}）满足b_ij = a_ji，则矩阵B是A的转置（transpose），记为B= A^T。

下图为一部分逆矩阵和矩阵转置的重要性质：

如果对于矩阵A，A = A ^T，那么称矩阵A是对称的（symmetric）。

1.5 矩阵和标量的乘法

矩阵和标量的乘法满足结合律（associativity），交换律（transpose）和分配律（distributivity）。具体如下图所示：

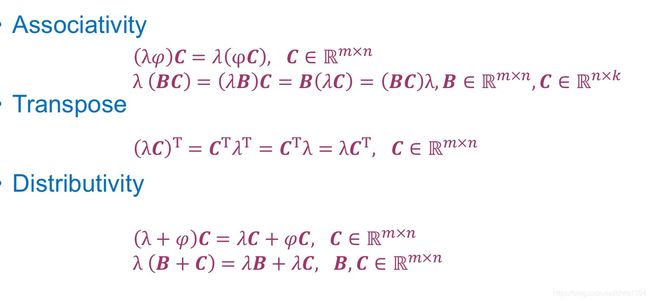
2. 高斯消元法

待补充

3. 向量空间

3.1 群（groups）

对于一个集合G，和一种运算⨂，满足G⨂G→G，即运算⨂对于G是闭运算，那么将（G，⨂）称为群（group）。一个群是由一个集合和一种运算法则组成。对于一个群，有以下性质，分别是封闭性，结合律，单位元素和逆元素：

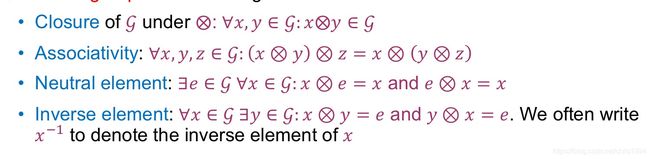
如果一个群还满足交换律条件∀x, y ∈ G, x⨂y = y⨂x ，那么这个群又称为阿贝尔群（Abelian group）。比如整数集合和加法就是一个阿贝尔群。而自然数集合和加法则不是一个群，因为缺失inverse element。

3.2 向量空间（vector space）

向量空间V是由一个集合v和两种运算组成，记为V=（v，+，·），其中运算+ ∶ V⨂V → V ， 运算· ∶ ℝ⨂V → V。一个向量空间包含分配律，结合律和自然元素三种性质。

在向量空间中的元素就是向量vectors，向量空间的neutral element就是零向量0 = [0,⋯, 0]^T。运算+就是向量的加法。上图中的λ是标量，运算· 是向量乘以标量。

3.3 向量空间的子空间

设U为向量空间 V 的一个非空子集，若U在 V 的加法及标量乘法下是封闭的，且零向量0 ∈ U，就称U为 V 的线性子空间（subspace）。因为U是封闭的（closure），所以∀x, y ∈ U, x + y ∈ U 而且 ∀x ∈ U, λ ∈ ℝ, λx ∈ U。对于向量空间V，V的所有子空间中最不重要的（trivial）是V自身和 {0} 。

3.4 向量空间的基底

对于一个向量空间V= （v ,+, ·），和v中一个子集合A = {x ₁， … ， x _k}，如果向量空间V中的每一个向量v都可以由x ₁， … ， x _k组合成，那么A就是V的一个生成集合（generating set）。A中所有线性组合（linear combinations ）的向量称为A的span。我们可以把V和A记为V = span[A]。

对于一个向量空间V和它的 generating set A，如果A已经是最小化的即不存在比A还小的集合是V的generating set，那么这样的A称为向量空间V的基底（basis），记为B。总结来说，B是向量空间V的基底，也是V的最小的生成集合，还是V中最大化的线性独立向量集合。最大化的线性独立（线性无关）向量集合意思是这个集合中每个向量都是线性独立（linearly independent），而且再加入任何向量都会使得这个集合不满足线性独立。

一个向量空间可以有多组基底，但是每个基底都有相同个数的基向量（basis vectors）。基向量的个数也称为向量空间V的维度（dimension），记为dim(V)。

向量空间的基底可以通过寻找最大线性无关向量集合来确定，具体方法是将表示向量空间的矩阵A进行高斯消元，得到倒三角矩阵，也就是行阶梯形矩阵（Row-Echelon Form）。这个矩阵中的pivot columns组成的spanning vectors就是这个向量空间的基底。详细例子见下图。

3.5 向量空间的秩

对于一个矩阵A∈R^{m * n}，A的所有行的相互独立向量个数和A的所有列的相互独立向量个数一样，那么这个个数就是A的秩（rank），记为rk(A)。而且A的转置矩阵的秩也等A的秩，即rk(A) = rk(A^T)。

对于一个方阵A∈R^{n * n}，当且仅当它的秩为n即rk(A)=n，矩阵A是可逆的（invertible），也叫regular。

对于一个等式Ax = b，这个等式是可解的当且仅当rk(A) = rk(A|b)，即A的秩等于A与b的增广矩阵的秩。增广矩阵A|b，又称广置矩阵，是在线性代数中系数矩阵的右边添上线性方程组等号右边的常数列得到的矩阵。

矩阵的秩可以通过将矩阵高斯消元之后pivot columns的数量得到。当一个矩阵A的秩等于在相同维度中所有矩阵所能达到的最大的秩时，这个矩阵A就是满秩的（full rank）。此时A的秩是矩阵行数和列数中较小值，即rk(A) = min (m, n) 。不是满秩的矩阵则称为rank deficient。

4 线性映射（linear mapping）

4.1 线性映射定义

对于两个向量空间V，W，当一个从V到W的映射（mapping）Φ:V → W满足∀x, y ∈ V, ∀λ,ψ ∈ ℝ : Φ( λx + ψy) = λΦ (x) + ψΦ(y)的条件，这个映射称为线性映射（linear mapping，也可以叫homomorphism）。线性映射包含两个性质：Φ (x + y )= Φ (x) + Φ(y) 和 Φ(λx) = λ Φ(x)。也可以从这两个性质判断一个映射是否是线性的。

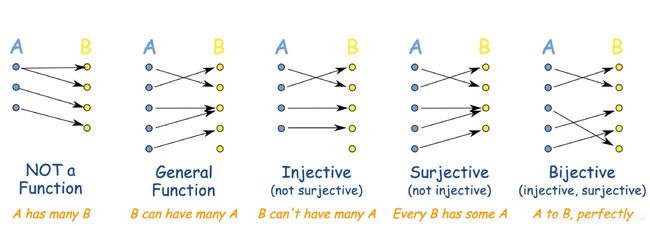
4.2 映射的种类

(1) 单射（injective）：当一个映射满足∀x, y ∈ V:Φ (x) = Φ(y) ⇒ x = y。
(2) 满射（surjective）：当一个映射满足Φ(V) = W 。
(3) 一一映射（bijective）：当一个映射同时满足单射和满射时。
下图对比了不同的映射：

根据映射是线性或者一一映射，可以将这个映射分成四类：（两个向量空间V，W）
(1) 同形（Isomorphism）: Φ: V → W 且这个映射是线性linear和一一映射bijective。
(2) 自同态（Endomorphism）: Φ: V → V 且这个映射是线性linear。
(3) 自同构（Automorphism）: Φ: V → V 且这个映射是线性linear和一一映射bijective。
(4) 标准映射（identity mapping）: id_v: V → V, 且映射中每个向量都是x → x。
(5) 同构（isomorphic）：V和W是同构的当且仅当dim(V)=dim(W)。

4.3 映射的矩阵表示

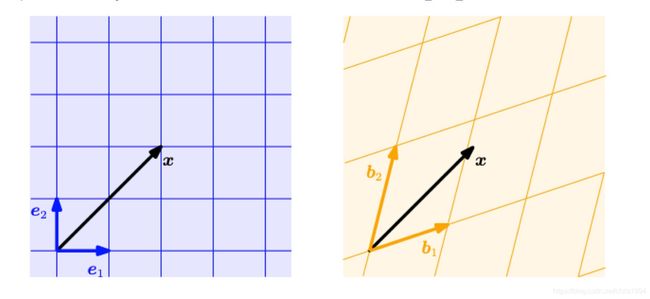
对于给定向量空间V和它的一组基底B = (b₁,…, b_n)，V中每一个向量x都有唯一确定的表达x = a₁*b₁ + …+ a_n*b_n。其中a₁到a_n称为x的坐标（coordinates）。同一个x在不同基底下有不同的坐标，比如下图中两组基底e和b，x的坐标就不一样。

我们可以使用这种坐标表示建立从一个向量空间到另一个向量空间的矩阵表示。给定向量空间V和W，它们各自的基底是B =(b₁,…, b_n)和C= (c₁,…, c_m)。可以建立一个线性映射Φ: V → W。对于j从1到n，有唯一的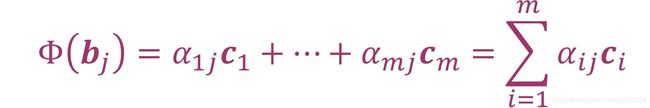
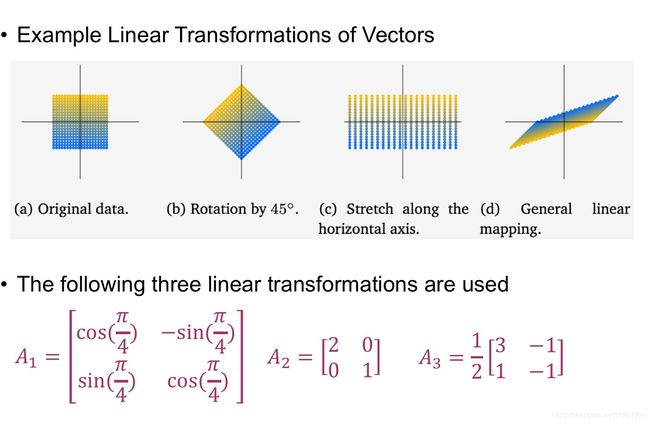
将其中系数a提出组成一个mn的矩阵A，这个矩阵就是从V到W的转移矩阵（transformation matrix）。对于V中的向量X ∈ V的坐标 和W中的向量Y = Φ x ∈ W 的坐标y，有y = Ax。使用转移矩阵可以进行向量的线性变化，如下图所示，进行了旋转，伸缩等三种变化：

4.4 基底转化（basis change）

一个线性映射Φ: V → W，V的两个基底是
W的两个基底是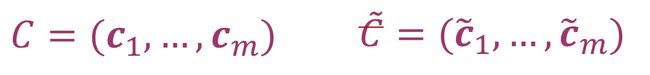
B和C的转移矩阵为A_Φ，B^ 和 C^ 的转移矩阵是A^_Φ。这两个转移矩阵关系是
其中S∈ ℝ^n*n是从B^ 到B的转移矩阵，T是从C^ 到C的转移矩阵。它们的关系如下图（根据给出的四组基底可以求出各自间的转移矩阵）：

5 映射空间（image）和核空间（kernel）

对于一个映射Φ: V → W， 它的核空间（kernel/null space）定义为：

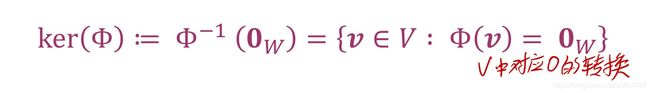
kernel是W中零向量在V中的对应向量。
而它的映射空间（image/range）定义为：

image是所有V中向量对应之后W的向量集合。V和W分别称为映射Φ的作用域（domian）和值域（codomain）。下图展示了kernel和image的具体对应关系：

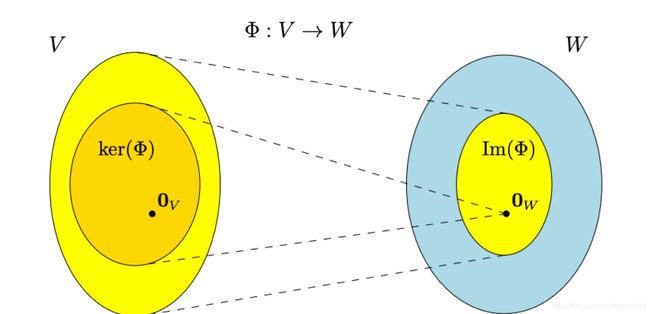
重要性质1：通过映射的image可以求转移矩阵A的秩，rk(A)=dim(Im(Φ))。而ker(Φ)则对应等式A*x=0的解的个数。
重要性质2：对应两个向量空间V和W以及它们的线性映射Φ: V → W ，均有dim(ker(Φ)) + dim(Im(Φ)) = dim(V)

6 仿射空间

6.1 仿射空间定义

仿射空间（affine space）是指没有原点（origin）的向量空间。仿射空间不包含向量子集合。
对于一个向量空间V，x₀是V中的一个向量，U是V的子空间。满足下面条件的子空间L叫做V的仿射子空间（affine subspace），也叫linear manifold：

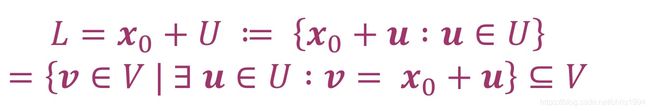
其中U被称为direction space，x₀是支撑点（support point）。

6.2 仿射变换

对于两个向量空间V和W，如果线性映射是Φ ∶ V → W，那么仿射变换（affine mapping）是x→a+Φ(x)。其中a是一个位移向量（translation vector）。线性变换的几何意义是图像的旋转和变形，仿射变换的几何意义是旋转和变性再加上位移。仿射映射保持几何结构不变。它们还保留了尺寸和平行度。

---

三、基础统计学知识

1 离散概率和连续概率

1.1 概率的几个重要概念

离散空间：在集合X上的离散拓扑是通过集合X的所有子集是开集而定义的，那么X是离散拓扑空间（简称离散空间）。在离散空间中，点都在特定意义下是相互孤立的。

概率质量函数（probability mass function）：给定一个离散目标空间（discrete target space）T，一个离散随机变量X取到特定值x（x∈T）的概率叫做概率质量函数，记为P(X=x)。概率质量函数可以看为一个特定点发生的概率。

累积分布函数（cumulative distribution function）：对于连续的目标空间，随机变量X的变化往往要用一个区间（interval）来估计，而不是一个点。为了方便，通常求X小于某一个特定值的概率，即P(X≤x)，这个概率称为累积分布函数。

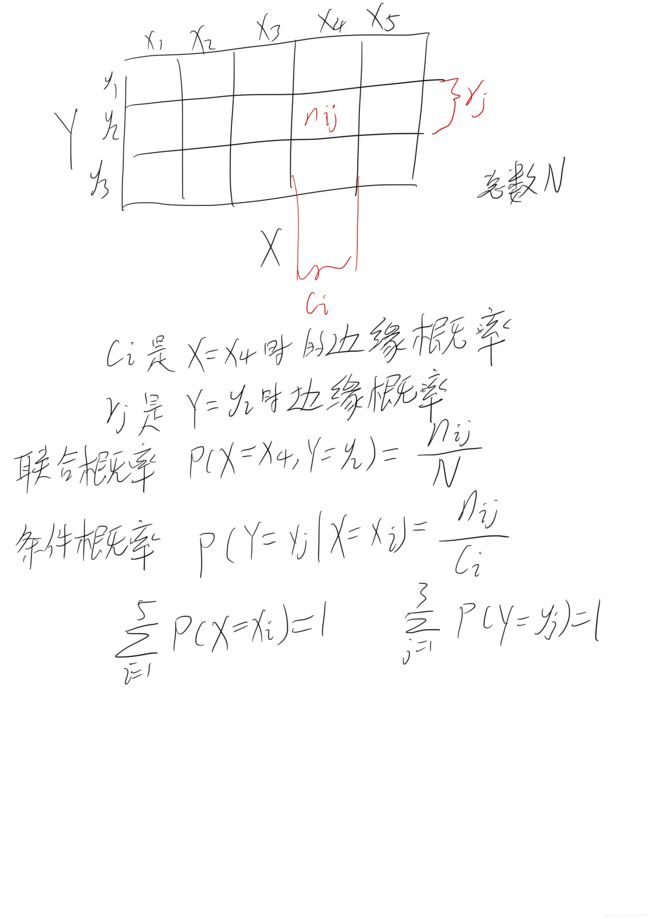
联合概率（joint probability）：X=x_i和Y=y_j两个事件同时发生的概率叫联合概率，记为P(X=x_i,Y=y_j)=n_ij/N。其中n_ij为事件x_i和y_j同时发生下状态的数量，N为事件总数。联合概率也可以写为p(x,y)。

边缘概率（marginal probability）：对于两个变量X和Y，当X=x发生下且与Y取值无关时，事件x的概率，记为p(x)。

条件概率（conditional probability）：当X=x已经发生的情况下，Y=y发生的概率叫做条件概率，记为p(y|x)。
下图举例说明了联合概率，边缘概率和条件概率：

概率密度函数（probability density function）：在连续分布空间中，连续随机变量X在某个特定点附近取到的可能性的概率叫概率密度函数，记为f(x)。对于任意x，f(x)≥0。
X在a≤X≤b这一区间中的概率可以用概率密度函数积分得到：

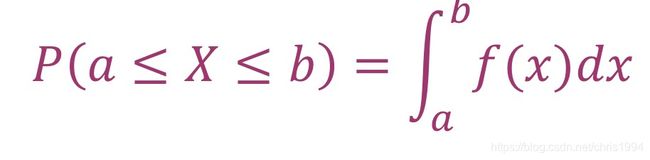
累积分布函数：对于连续随机变量X小于x时的概率可以从上式变化得到，令a为负无穷，b=x就可以得到，一般情况下对于X∈R^D，X=x的累积分布函数是：

1.2 概率的加法和乘法，贝叶斯公式

假设p(x,y)是x和y的联合概率， p(x)和 p(y)分别是x和y的边缘概率， p(y|x)是x条件下y的条件概率。
概率的加法法则（sum rule）是（又被叫做marginalization property边沿性质）：

概率的乘法法则（product rule）：是指y在x条件下的条件概率乘x条件的概率得到x和y的联合概率，用数学式表示就是p(x,y)=p(y|x)*p(x)。同样该联合概率也可以让y成为条件先发生，即p(x,y)=p(x|y)*p(y)。

贝叶斯法则：通过x和y联合概率的两种表达方式等价，可以推出下面公式（将p(y)移到另一侧作为分母）

其中p(x)是先验概率（prior），它是我们在观察任何数据之前对未观察到的（潜在的）变量x的主观先验知识。p(y|x)是似然概率（likelihood），描述了x和y的相关性，也叫x关于y的相似程度。p(x|y)是后验概率，它是贝叶斯统计中的兴趣量，因为它准确地表达了我们所感兴趣的东西。

边缘似然概率（marginal likelihood/evidence）：将似然概率p(y|x)对于x求积分可以得到y的边缘似然概率，数学式表示为：

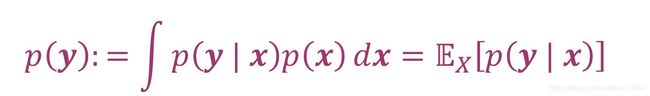
2 统计学概念

2.1 均值和方差

期望值（expected value）：对于函数g：ℝ⟶ℝ，单一连续随机变量X∼p(x)的期望值是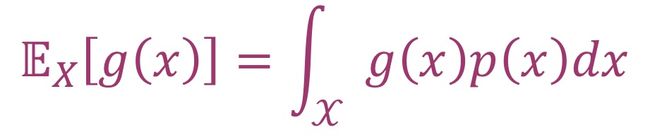
同样的，对于离散随机变量X∼p(x)的期望值是

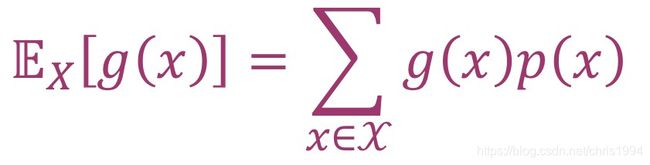
更一般的情况下，将X扩展到D维空间里N个变量组成，g(x)的期望值是D维中每一维依次求期望值所得，数学表达为：

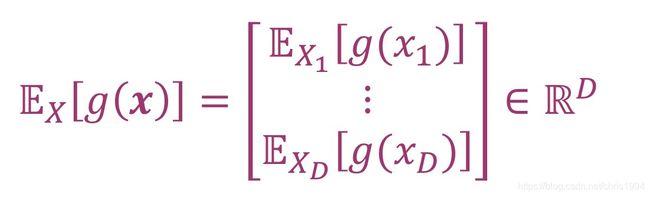
平均值（mean）：随机变量X的平均值可以通过当g(x)取平均状态x∈R^D时求得，数学表达为：

中位数（median）：在所有已经排序的数值中位于中间位置的数值。对于非对称分布或长尾分布，中位数提供了一个比平均值更接近人类直觉的典型值的估计。或者说，中位数比平均值更具有鲁棒性（robust）。

众数（mode）：出现次数/频率最多的数值。对于离散随机变量，众数定义为出现频率最高的x值。对于连续随机变量，众数定义为密度p(x)的峰值。

协方差（covariance）：两个单一随机变量X，Y的协方差是它们偏离各自平均值的乘积的期望值，数学表达为：

当X和Y呈现线性关系时，上式可以化简为：

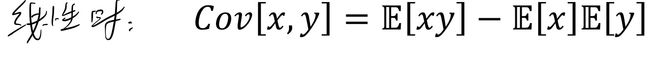
方差（variance）：对同一个变量X和它自身求协方差，得到的就是X的方差。假设X的平均值向量为μ，状态x∈R^D，那么方差可以表示为V[x] = Cov[x,x]，又可以将它拆分到D维中得到每一个维度之间对应的协方差，由这些D*D个协方差构成的矩阵叫做协方差矩阵（covariance matrix ）：

相关性系数（correlation）：相关系数是将协方差标准化之后的结果，是相对数值，没有单位，范围 从-1 到 +1。如果x增长时y也增长则它们的相关性系数为正。

在实际应用中，数据是有限且不准确的，所以之前理论上的均值和方差在实际应用中几乎无法得到。代替的，我们可以使用经验均值和经验方差进行近似求解。

经验均值（empirical mean）：经验均值是每个变量的观测值的算术平均值，数学表达为

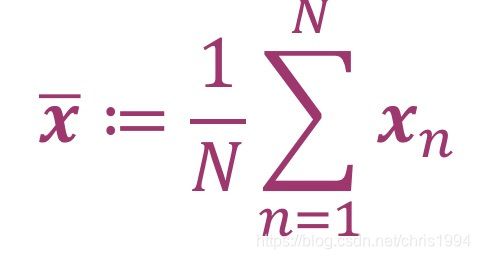
经验方差（empirical covariance ）：利用经验均值替代均值之后求得的方差，经验方差是对称，正半限定（positive semi-definite）。数学表达为

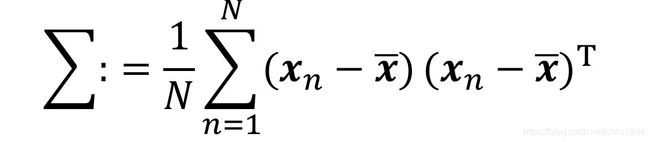
总结来说，方差现在有三种表达式，分别是使用期望值µ计算得到

也可以使用方差的原始公式计算（raw-score formula）得到

还可以使用经验方差进行计算得到

2.2 均值和方差的加减法

对于两个随机变量X和Y的状态值x和y∈R^D，它们的均值和方差可以进行加法或减法运算，运算公式如下：

当我们知道X的均值为μ，协方差矩阵为Σ，以及y是x的仿射变换y=Ax+b。那么y的均值和方差也可以求得

而且x和y的协方差为Cov[x,y]=Σ*A^T。

2.3 线性独立

统计学上的相互独立：对于两个随机变量X，Y，X和Y的相互独立的（statistical independent）当且仅当p(x,y)=p(x)*p(y)。x和y的相互独立可以理解为y的值中不带有任何有关x的信息。

当x和y相互独立时存在下列关系：

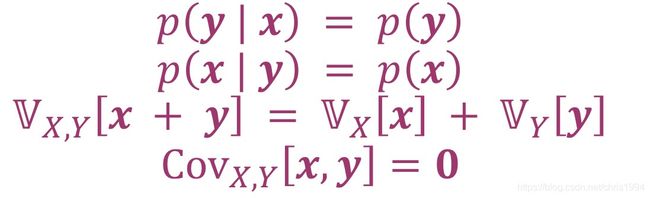
其中，虽然x和y相互独立之后满足它们的协方差为零，但是当x和y的协方差为零时它们不一定相互独立。因为协方差只测量线性相关性。因此，非线性相关的随机变量都可能协方差为零。

条件独立（conditionally independent）：两个随机变量X和Y，如果它们在给定条件变量Z下满足p(x,y|z)=p(x|z)*p(y|z)，z是Z中所有可能的状态，那么X和Y就是在Z的的条件下相互独立（conditionally independent），记为X ⫫ Y|Z。 根据概率的乘法法则可以把p(x,y|z)=p(x|z)*p(y|z)的左边写成等式p(x,y|z)=p(x|y,z)*p(y|z)，再把两个等式合并消除p(y|z)可以得到p(x,y|z)=p(x|z)，这也是条件独立的另一种判断方式。p(x,y|z)=p(x|z)可以理解为当给定条件z时，y的值无法改变x的值。

2.4 内积

随机向量可以看为分布在一个向量空间中的向量，它们之间存在向量相乘和向量夹角。
内积（inner products）：对于两个均值为0的随机变量X和Y，它们的内积定义为

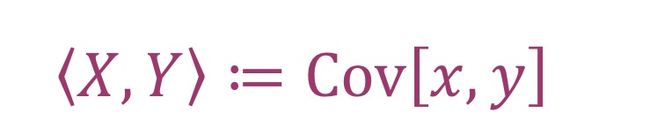
标准差（standard deviation）：随机变量X的标准差就是它的方差开平方，数学表达为

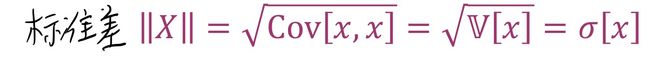
X和Y的向量夹角θ：θ的cos余弦值就是X和Y的相关系数，从这里可以求得θ

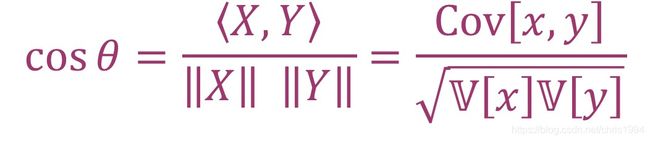
2.5 高斯分布

高斯分布（Gaussian distribution）：它是最常见的连续随机变量的分布，也称为自然分布（normal distribution）。对一个单一随机变量x，它的高斯分布的密度函数为（其中X的均值为μ，标准差为σ）

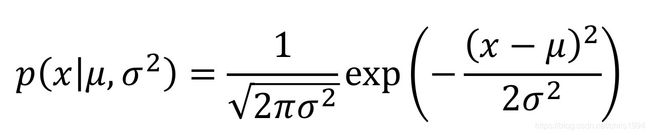
多元高斯分布（multivariate Gaussian distribution ）：当变量X是多维的，它的高斯分布为下式（其中X的均值为μ，协方差矩阵为Σ）。多元高斯分布记为p(x) = N( x| μ, Σ) 或X ∼ N(μ, Σ).

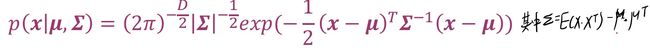
标准正态分布（standard normal distribution）：当高斯分布的均值为0，协方差矩阵为单位矩阵即μ = 0 且Σ = I时，这样的高斯分布叫做正态分布。

对于两个高斯分布X和Y，X和Y的联合（concatenated）分布也是高斯分布，且概率为

其中Σ_xx=Cov[x,x]和Σ_yy=Cov[y,y]是x和y的方差，也叫边缘协方差矩阵（marginal covariance matrices ）。Σ_xy=Cov[x,y]是x和y的交叉协方差矩阵（cross-covariance matrix）。

x和y的条件概率p(x|y)也是高斯分布，它的概率以及均值方差为

两个高斯分布相乘得到的依然是高斯分布，它的概率c为（其中a和A，b和B是相乘之前的两个高斯分布的均值和方差）

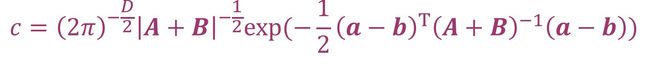
如果两个高斯分布是相互独立的，那么它们相加得到的也是高斯分布，新高斯分布的均值和方差都是之前各自均值和方差之和。和的高斯分布概率为p(x + y) = N( μ_x+μ_y, Σ_x+Σ_y)。

如果变量Y是高斯分布X经过仿射变换得到，即y=Ax+b，那么y也是高斯分布，且它的均值和方差为（其中X的均值为μ，协方差矩阵为Σ）

---

四、机器学习的基础知识

1 模型与数据

1.1 机器学习组成

一个机器学习系统由三部分组成：数据（data），模型（models）和学习（learning）。数据集通常分为三部分：训练集（training set），验证集（validation set）和测试集（test set）。训练集用作模型的训练与学习，验证集用于模型的选取，测试集用于模型正确率的测试，具体将在1.5小节说明。

通过在训练集数据上的学习（learning）得到模型，然后在测试集数据上应用进行预测（prediction）。机器学习的目标是得到一个好的模型，好的模型包括：高的分类正确率（Classification accuracy），与真实值偏差小，运行测试时间短且有效，合适的模型大小。

1.2 数据化向量

机器学习的数据需要经过计算机的处理，所以这些数据是可以量化的（numerical），通常数据需要转换成向量的模式输入计算机。以下面数据为例

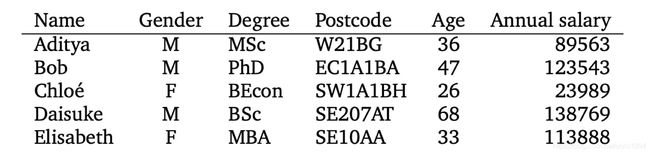
表格中每一行（row）为一个实例（instance）比如Bod的性别，学位等信息；每一列为一个特征（feature），比如性别（gender），年龄（age）。这些数据信息有些事数字，比如年龄，可以直接量化，输入计算机。但是有些是含有特定意义的字符串（string），这些字符串计算机是无法理解的，需要把它们量化，即转化成数字。像性别，只有男女两种，可以使用1
和0表示。但是像邮编（postcode），含有未知数目，但是它们是离散的，可以使用独热编码（one-hot code）将它们数据化，具体在1.4小节讨论。

假设表格中有N行，D列，即数据集含有N个例子或者数据点（data point），使用x_n表示这N个数据点，每一个数据点都要转化为一个向量，总共N个向量。每一个数据点都是D维的，即含有D个特征，所以数据可以转化为D维向量（D-dimensional vector）。这些数据转化的向量就可以输入计算机进行学习。但是不是所有数据点的所有特征都是有用的或有效的，其中无关数据或错误数据需要在模型学习之前进行剔除或者其他处理，这一步就是在机器学习之前的预处理过程（pre-processing），具体将在1.6小节说明。

如果有一列特征被当做标签（label），那么这组数据就可以进行有监督学习，而这一列特征会被单独提取出来，作为目标值y_n。每一个数据点都有对应的目标值y_n，和x_n组成一对实例-标签对（example-label pairs），即（x_n，y_n），这样的实例-标签对总共有N个。在学习模型以及测试中，输入的是这些实例-标签对。

1.3 模型的参数

模型在通过机器学习得到之后可以用来预测新的数据（测试集），这时模型实现的就是预测功能（predictive function），这个模型又叫做预测器（predictor）。模型输入的一组D维向量x_n，输出的一般是一个实数的标量（real-valued scalar）。机器学习最常见的两个功能就是分类和回归，模型对应输出的分类的类别和回归线的取值。这个过程可以使用f(x)表示，即f: ℝ^D→ ℝ。

以线性模型为例，详细说明一下模型。假设模型为f(x)=θ^Tx+θ₀。假设当x=60时我们f(x)求得的是100，100是模型预测值。但是真实应用中，观察到的数据是存在误差或噪音的，所以我们实际得到的数据是由真实数据（true underlying data）和噪音（noise）共同组成，即x’ = x+n，n是噪音。当把x‘输入到模型中计算得到的预测值也应该是存在误差的，是不确定的。比如当x为6预测是100，如果噪音n=10，那么输出可能就是110。一般情况下噪音是正态分布的，意味着n大概率为0，所以我们输出的预测值也是大概率为100。此时我们可以使用概率来表示输出的预测值，即预测值是以正确值（比如100）为均值的正态分布。这样的模型叫做概率性模型（probabilistic models）。

机器学习的目的是找到一个最合适的模型，使得预测值（概率性模型中正态分布的均值）和真实值的误差最小（一般是方差最小，这个误差就是损失函数，在1.7小节说明）。模型实际上是不确定系数（参数）的数学等式，所以机器学习就是在寻找最优的参数（parameters）。机器学习使用三个阶段来寻找最优参数：预测或推断（Prediction or inference），训练或参数估计（Training or parameter estimation）和超参数调整或模型选择（Hyperparameter tuning or model selection）。

预测阶段：使用已经训练好的预测器在测试集中进行预测。
训练阶段：使用训练集数据调整参数使得输出误差最小，即经验风险最小（empirical risk minimization）。在风险最小时的参数即有可能是最优参数。但是数据存在局限性，训练集上的最优不代表整体数据上的最优，甚至可能出现训练集上效果很好但是测试集效果很差（过拟合现象）。这时要使用验证集调整选取参数，也可以使用正则化减小过拟合现象（详细在1.8小节说明）。
超参数微调阶段：模型中有一些参数是无法通过机器学习得到的，需要人为提前设定，比如神经网络中的层数，正则化中的权重，聚类中的类总数。这些参数称为超参数（Hyperparameter）。选取不同超参数或者模型的过程叫做模型选择（model selection）。

超参数和参数的不同：参数是通过数据学习得出的，它们是量化最优的（numerically optimized）。而超参数是通过经验决定的，需要寻找尝试不同模型或技术。

1.4 独热编码

独热编码（one-hot code）：又称为一位有效编码，主要是采用N位状态寄存器来对N个状态进行编码，每个状态都由它独立的寄存器位，并且在任意时候只有一位有效。它会将数据映射到整数值，然后把整数改编为二进制向量。在python中，独热编码的程序存在sklearn中preprocessing库中，使用fit()输入数据，使用transform()转换数据。该函数具体为sklearn.preprocessing.OneHotEncoder(*, categories='auto', drop=None, sparse=True, dtype=, handle_unknown='error') 。其中categories一项表示特征的取值，默认auto即输入编码数据的特征取值；drop是用于删除每个要素的一个类别的方法，默认none不删除；sparse若为True时，返回稀疏矩阵（在矩阵中，若数值为0的元素数目远远多于非0元素的数目，并且非0元素分布没有规律时，则称该矩阵为稀疏矩阵），否则返回数组；dtype是输出数据类型，默认为浮点型float；handle_unknown代表在转换过程中，如果出现不知道的分类特征时，选择抛出错误或直接忽略。

from sklearn import preprocessing  
   
OneHotCode = preprocessing.OneHotEncoder()  
OneHotCode.fit([[0,3],[1,1],[0,1],[1,2]])   # Fit OneHotEncoder to X.
output = OneHotCode.transform([[1,3]]).toarray()  #Transform X using one-hot encoding.
#上述功能可以使用fit_transform(X[, y])一起实现，fit_transform()用处是Fit OneHotEncoder to X, then transform X.

独热编码要求数据的每个类别之间相互独立，它的目的是将类别变量转换为机器学习可以量化的向量。

1.5 训练集，验证集和测试集

在得到数据集后，要将数据集拆分为训练集和测试集，有时还会有验证集。一般情况下，随机选择百分之50到百分之70的数据作为训练集，其余为测试集。当存在验证集时，我们需要单独再提取一部分数据作为验证集。在机器学习过程中，我们仅使用训练集和验证集，注意测试集不参与训练过程；在测试模型阶段才使用测试集，我们把预测器应用在测试集上以计算得到更加通用的误差（generalization error）。训练集和验证集在模型训练过程中一起使用，它们之间要保证没有重复数据，即训练集和验证集的交集为空集。而且一般情况下训练集数据多于验证集，因为小的验证集会使得预测结果的更不稳定，结果的方差更大，更容易得到通用的模型。产生验证集的方法一般是在划分出训练集之后使用交叉验证（Cross-validation）得到。

交叉验证：对给定的建模样本进行交叉验证，将数据分为等量的K份，取出大部分样本（k-1份数据）作为训练集建立模型，留下一小部分样本（一份数据）作为验证集用刚建立的模型进行预测，计算出小部分样本的预测误差并记录其平方和。然后循环替代使用其他份的数据作为验证集，重复上述步骤。这一过程一直持续到所有样本预测一次且仅预测一次。利用验证集对训练模型进行测试，作为评价模型分类的性能指标。然后根据这个指标调整参数，就可以执行提前终止或退出操作。这可以减少过拟合并提高测试集上模型的精度。这种将数据分为k份循环作为验证集的方法叫k折交叉验证（K-fold cross-validation）。下图展示了k=5时每次训练集和验证集的划分

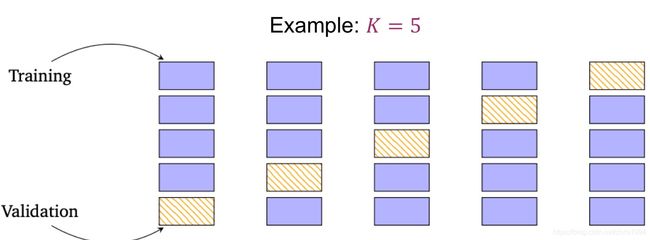
k折交叉验证使用在数据样本较少的情况下，当数据足够多时，可以直接将数据分为训练集，验证集和测试集。k折交叉验证中K越大，每次投入的训练集的数据越多，模型的Bias越小。但是K越大，又意味着每一次选取的训练集之前的相关性越大（考虑最极端的例子，当k=N，N是数据总数，每次都训练数据几乎是一样的）。而这种大相关性会导致最终的test error具有更大的Variance。一般选择k=5或10。

k折交叉验证可以使用sklearn.model_selection库中的KFold函数将数据分成训练集和测试集。具体函数为sklearn.model_selection.KFold(n_splits=5, *, shuffle=False, random_state=None)，其中使用n_splits确定k的取值。

from sklearn.model_selection import KFold

X = ["a", "b", "c", "d"，"e"]
kf = KFold(n_splits=5)
for train, test in kf.split(X):    #use split() to generate indices to split data into training and test set.
	print(train)
kf.get_n_splits(X)     #Returns the number of splitting iterations in the cross-validator

留一验证（LeaveOneOut）：是一个简单的交叉验证。每个学习集都是通过抽取除一个样本外的所有样本来创建的，测试集就是遗漏的样本。留一验证是特殊的当验证集每次仅选取一个数据点的k折交叉验证。

1.6 预处理过程

预处理过程（Preprocessing）：学习算法受益于数据集的标准化。如果集合中存在一些异常值，学习的模型可能存在较大偏差。预处理过程使用定标器（scalers），变换器（transformers）和规范化器（normalizers）等将原始特征向量转换为更适合后续预测器的表示。

1. 缺省值处理

预处理过程要先把其中的缺失数据应该进行特殊处理。一般在读取数据某些特征时会有缺失值，如果缺失值过多基本上可以直接去除掉这一列，在缺失值不多的情况下可以用一些方法处理，比如插入0、平均值、中位数值等等。下面介绍常见的五种缺省值处理办法。

直接删除缺省值：若变量的缺失率较高（大于80%），覆盖率较低，且重要性较低，可以直接将变量删除。一般删除有缺省值的数据点的所有特征，这样会带来数据量的减小。如果是某个特征下的缺失数据较多，而这个特征对整体而言并不重要，可以把这个特征直接删除。直接删除的办法虽然简单，但是会有信息丢失，当数据集比较大时可以使用。

均值插补：缺失值可以使用事先约定的常量值（比如0）进行插补，替换缺省值，也可以使用缺失值所在列的统计信息（平均值、中值值或最频繁值）。在python提供的机器学习库sklearn.impute中可以使用SimpleImputer函数进行均值插值，也可以叫做单变量特征插补（Univariate feature imputation）。因为均值插补应用的是缺失值所在列的统计信息，所以用于填补的数据都来自同一个变量，故叫单变量特征插补。具体函数为sklearn.impute.SimpleImputer(*, missing_values=nan, strategy='mean', fill_value=None, verbose=0, copy=True, add_indicator=False)，其中missing_values是缺少值的占位符，填入缺省值的种类（比如float, str），如果是pandas数据中的null缺省值则要设置为np.nan；strategy是插值策略，默认使用均值插补，也可以使用众数和中位数插补；fill_value是让缺省值为0或null；verbose控制输入程序的详细程度；copy用于复制副本；add_indicator是否MissingIndicator转换将堆叠到输入器变换的输出上。

import numpy as np
from sklearn.impute import SimpleImputer
imp_mean = SimpleImputer(missing_values=np.nan, strategy='mean') #设置SimpleImputer的参数，使用均值插补
imp_mean.fit([[7, 2, 3], [4, np.nan, 6], [10, 5, 9]])  #向插补器输入数据，生成SimpleImputer()模型
X = [[np.nan, 2, 3], [4, np.nan, 6], [10, np.nan, 9]]  #原数据X
print(imp_mean.transform(X))  #将X进行转换并打印
#结果是   [[ 7.   2.   3. ]
#        [ 4.   3.5  6. ]
#        [10.   3.5  9. ]]

多变量特征插补（Multivariate feature imputation）：多变量特征插补也可以叫做多重插补，迭代插补，它是基于贝叶斯估计。每一个缺省值可以估计出可能的预估值，预估值会有多个，它们都可以来插补缺省值，产生多个完整数据集，然后根据不同数据集的训练预测表现选出效果最好的数据集，作为最终的插补。多变量特征插补可以理解为单变量特征插补进行循环迭代选取最优。可以从已有的完整数据训练一个回归器，利用回归器得到缺省值的预估值，然后进行完整数据的训练和评估，根据评估结果调整回归器，进行下一次迭代。这个方法目前还在实验阶段，目前没有一个很完善的回归模型。在python提供的机器学习库sklearn.impute中可以使用IterativeImputer函数进行多变量特征插补，具体为sklearn.impute.IterativeImputer(estimator=None, *, missing_values=nan, sample_posterior=False, max_iter=10, tol=0.001, n_nearest_features=None, initial_strategy='mean', imputation_order='ascending', skip_complete=False, min_value=- inf, max_value=inf, verbose=0, random_state=None, add_indicator=False)，其中estimator设置在循环插补的每个步骤中使用的估计器，missing_values是缺少值的占位符，sample_posterior表示是否从每个插补的拟合估计量的（高斯）预测后验值中取样，max_iter最大迭代次数，initial_strategy选择插补策略（默认均值），random_state选择伪随机数发生器的种子（常用种子0到42），其余可以调整升序降序等。

import numpy as np
from sklearn.experimental import enable_iterative_imputer
from sklearn.impute import IterativeImputer
imp_mean = IterativeImputer(random_state=0) #伪随机数发生器选择0号种子
imp_mean.fit([[7, 2, 3], [4, np.nan, 6], [10, 5, 9]]) #向插补器输入数据，生成IterativeImputer(random_state=0)模型
X = [[np.nan, 2, 3], [4, np.nan, 6], [10, np.nan, 9]] #原数据X
imp_mean.transform(X)
#插补结果是  array([[ 6.9584...,  2.       ,  3.        ],
#               [ 4.       ,  2.6000...,  6.        ],
#               [10.       ,  4.9999...,  9.        ]])

最近邻法插补（Nearest neighbors imputation）：使用K近邻方法进行缺省值补充。当之前的单变量特征插补或多变量特征插补遇到缺省值相关的数据不足，即缺失数据所在行列信息不足，或者数据直接关联不强时，这两种方法的效果都不好。此时就可以使用最近邻法插补。最常见的例子，一张图像中的部分像素点数据缺失，可以使用周围像素点的数据，根据KNN进行分类判断，选取距离最小的数据进行代替缺省值。KNN使用缺失值的欧几里德距离度量方法来查找最近的邻居，如果有多个邻居可以取平均，也可以结合关联插值选取其中关联程度最大的。在python提供的机器学习库sklearn.impute中可以使用KNNImputer函数进行最近邻法插补，具体为sklearn.impute.KNNImputer(*, missing_values=nan, n_neighbors=5, weights='uniform', metric='nan_euclidean', copy=True, add_indicator=False)。其中missing_values是缺少值的占位符，n_neighbors是用于插补的相邻样本数，weights用于预测的权函数（可以是uniform权重一样，也可以是distance按距离的倒数加权点即近点的影响大），metric用于搜索邻居的距离度量，其余与IterativeImputer函数类似。

import numpy as np
from sklearn.impute import KNNImputer
X = [[1, 2, np.nan], [3, 4, 3], [np.nan, 6, 5], [8, 8, 7]] #原数据X
imputer = KNNImputer(n_neighbors=2) #选择缺省值的两个邻居进行插补
imputer.fit_transform(X) #输入数据X并进行转换，输出结果
#插补结果是  array([[1. , 2. , 4. ],
#               [3. , 4. , 3. ],
#               [5.5, 6. , 5. ],
#               [8. , 8. , 7. ]])

标记插补值（Marking imputed values）：这种方法将数据集转换为相应的二进制矩阵，查看数据集中是否存在缺失值，然后进行插补。标记插补值是将二进制转换和缺失值插补结合。有些缺失值在经过二进制转换之后为0，代表它不提供信息，可以不考虑。而对于二进制转换之后的缺失值继续进行插补。在python提供的机器学习库sklearn.impute中可以使用MissingIndicator函数进行标记插补，具体为sklearn.impute.MissingIndicator(*, missing_values=nan, features='missing-only', sparse='auto', error_on_new=True)，其中missing_values是缺少值的占位符，features代表输入掩码是代表全部特征还是一个子集特征，sparse代表输入的掩码格式是稀疏还是密集。

import numpy as np
from sklearn.impute import MissingIndicator
X1 = np.array([[np.nan, 1, 3],
                [4, 0, np.nan],
                [8, 1, 0]])
X2 = np.array([[5, 1, np.nan],
                [np.nan, 2, 3],
                [2, 4, 0]])
indicator = MissingIndicator()
indicator.fit(X1)  #进行数据X1输入生成MissingIndicator()，生成掩码
X2_tr = indicator.transform(X2) #将X2进行插补
#X2的插补结果是 array([[False,  True],
#                 [ True, False],
#               [False, False]])

2. 数据编码

预处理过程然后把训练采集的数据进行量化处理，转化为机器可以识别计算的数据，这一过程叫做编码（encoding）。对于简单的数据也可以使用二元化（比如大于0的转化为，其余为0）。二元化的编码器在python的经典机器学习库sklearn.preprocessing中有Binarizer函数对应。具体为sklearn.preprocessing.Binarizer(*, threshold=0.0, copy=True)，其中threshold表示低于或等于此值的要素值将替换为0，高于此值的要素值将替换为1；copy设置为False以执行就地二值化并避免复制。

from sklearn.preprocessing import Binarizer
X = [[ 1., -1.,  2.],        #原始数据
     [ 2.,  0.,  0.],
     [ 0.,  1., -1.]]
transformer = Binarizer().fit(X)   #输入x，但是无输出
transformer.transform(X)   #将X进行二元化
 #编码结果是array([[1., 0., 1.],
 #          [1., 0., 0.],
 #         [0., 1., 0.]])

更普通的编码可以将简单的字符串（原始数据）转化为输入向量。常见的编码器有LabelEncoder（将标签label转化为向量，即将分类转换为分类数值）和OrdinalEncoder（将特征编码，能够将分类特征转换为分类数值）。这两个编码器在sklearn.preprocessing库中具有对于函数。LabelEncoder对应函数为sklearn.preprocessing.LabelEncoder，该函数对目标标签进行编码，使其值介于0和n_classes-1之间。

from sklearn import preprocessing
le = preprocessing.LabelEncoder()  #导入LabelEncoder函数
le.fit([1, 2, 2, 6])  #输入数据，无输出
le.transform([1, 1, 2, 6])  #进行标签转化
#输出结果是array([0, 0, 1, 2]...)

#如果对字符串进行编码
le.fit(["paris", "paris", "tokyo", "amsterdam"])
le.transform(["tokyo", "tokyo", "paris"])
#输出结果是array([2, 2, 1]...)

OrdinalEncoder对应函数为sklearn.preprocessing.OrdinalEncoder(*, categories='auto', dtype=, handle_unknown='error', unknown_value=None)，其中categories是定义每个功能的类别，”auto”会根据训练数据自动确定类别；dtype是所需的输出数据类型；handle_unknown当设置为“错误”时，如果在转换过程中存在未知的分类特征，则会引发错误。

from sklearn.preprocessing import OrdinalEncoder
enc = OrdinalEncoder()    #载入OrdinalEncoder函数
X = [['Male', 1], ['Female', 3], ['Female', 2]]   #原始数据
enc.fit(X)  #输入数据，无输出
enc.categories_
#输出编码器的分类结果[array(['Female', 'Male'], dtype=object), array([1, 2, 3], dtype=object)]
enc.transform([['Female', 3], ['Male', 1]])
#输出编码结果是array([[0., 2.],
#       [1., 0.]])

适合最普通的数据可以使用1.4节提到的独热编码。使用sklearn.preprocessing.OneHotEncoder函数，详细见1.4节。

from sklearn.preprocessing import OneHotEncoder
enc = OneHotEncoder(handle_unknown='ignore')
X = [['Male', 1], ['Female', 3], ['Female', 2]]  #原始数据
enc.fit(X) #输入数据，无输出
enc.categories_
#输出编码器的分类结果[array(['Female', 'Male'], dtype=object), array([1, 2, 3], dtype=object)]
enc.transform([['Female', 1], ['Male', 4]]).toarray()
#输出编码结果是array([[1., 0., 1., 0., 0.],
#       [0., 1., 0., 0., 0.]])

3. 标准化处理

将数据编码完成后得到了可量化的输入向量，然后预处理过程会将这些向量进行标准化，归一化，将所有数据投射到同一个数量级上。这一步就是利用定标器（Scaler）进行数据标准化。下面介绍常用的四种定标器。

StandardScaler定标器：最常用的一种定标器，主要把数据删除平均值并将数据缩放为单位方差。StandardScaler处理之后的数据在坐标中处在原点附近，这种数据的均值为0，方差为1，更加单位化，消除了特征范围的影响，适用于大部分模型学习。但是计算均值和方差时会受到离群值的影响。当数据存在较大的离群值时，方差也会较大，那么缩减之后的数据范围可能较小，比如在[-0.1,0.1]之间。所以StandardScaler不能保证在存在异常值的情况下平衡的特征尺度。StandardScaler定标器的数学公式是z = (x - u) / s，x是原始数据，u是平均值，s是方差。

StandardScaler定标器在sklearn.preprocessing库中对应StandardScaler函数。具体为sklearn.preprocessing.StandardScaler(*, copy=True, with_mean=True, with_std=True)。其中copy设置为False以执行就地行规范化并避免复制，with_mean如果为真，在缩放之前请先将数据居中，进行中心化需要构建一个密集矩阵，with_std如果为真，则将数据缩放为单位方差。

from sklearn.preprocessing import StandardScaler
data = [[0, 0], [0, 0], [1, 1], [1, 1]] #原始数据
scaler = StandardScaler()  #载入StandardScaler定标器
scaler.fit(data) #向定标器输入数据并计算平均值和标准差，用于以后的定标。
print(scaler.mean_) #打印数据每个特质的均值
#平均值是[0.5 0.5]
print(scaler.transform(data))  #通过中心（均值）和缩放（除以方差）执行标准化
#缩放结果是[[-1. -1.]
#         [-1. -1.]
#         [ 1.  1.]
#         [ 1.  1.]]
print(scaler.transform([[2, 2]]))
#缩放结果是[[3. 3.]]

MinMaxScaler定标器：通过将每个特征缩放到给定范围来变换特征（输入的数据），可以用于替换StandardScaler。该定标器根据所有特征的最大值和最小值缩放和转换每个特征，使得其在训练集中的给定范围内，例如在0和1之间。转换公式是X_std = (X - X.min(axis=0)) / (X.max(axis=0) - X.min(axis=0))；X_scaled = X_std * (max - min) + min。其中，min和max分别是所有输入数据范围的最小值和最大值。

MinMaxScaler定标器在库中sklearn.preprocessing对应MinMaxScaler函数，具体为sklearn.preprocessing.MinMaxScaler(feature_range=0, 1, *, copy=True, clip=False)。其中feature_range是所需的转换数据范围，copy设置为False以执行就地行规范化并避免复制，clip设置为True可将保留数据的转换值剪裁到提供的特征范围。

from sklearn.preprocessing import MinMaxScaler
data = [[-1, 2], [-0.5, 6], [0, 10], [1, 18]] #原始数据
scaler = MinMaxScaler() #载入MinMaxScaler定标器
scaler.fit(data) #向定标器输入数据并计算用于缩放的最小值和最大值。
print(scaler.data_max_) #打印每个特征中的最大值，如果是data_min_则打印最小值
#最大值结果是[ 1. 18.]
scaler.transform(data) #根据特征范围缩放数据data的特征。
#缩放结果是[[0.   0.  ]
#        [0.25 0.25]
#        [0.5  0.5 ]
#        [1.   1.  ]]
scaler.transform([[2, 2]]) #缩放特定数据[[2, 2]]
#缩放结果是[[[1.5 0. ]]

Maxabscaler定标器：与MinMaxScaler定标器类似。将每个特征的最大绝对值缩放到单位大小，即maxabscaler将每个属性值除以该属性的绝对值中的最大值。它不会移动或集中数据，因此不会破坏任何稀疏性。所以这个定标器可以用于稀疏矩阵。

Maxabscaler定标器在sklearn.preprocessing库中对应MaxAbsScaler函数。具体为sklearn.preprocessing.MaxAbsScaler(*, copy=True)，其中copy设置为False以执行就地行规范化并避免复制。

from sklearn.preprocessing import MaxAbsScaler
X = [[ 1., -1.,  2.],  #原始数据
      [ 2.,  0.,  0.],
      [ 0.,  1., -1.]]
transformer = MaxAbsScaler().fit(X) #向定标器输入数据并计算缩放所用的最大绝对值。
transformer.transform(X) #将数据进行缩放
#缩放结果是array([[ 0.5, -1. ,  1. ],
#             [ 1. ,  0. ,  0. ],
#             [ 0. ,  1. , -0.5]])

Normalizer（正则化）定标器：归一化（正则化）是将单个样本缩放为单位范数的过程。归一化有助于使用二次型（如点积或任何其他内核）来量化任何一对样本的相似性。归一化器将每个样本的向量重新扫描为单位范数，而不依赖于样本的分布。Normalizer接受来自稀疏的作为输入。对于稀疏输入，Normalizer在输入之前会将数据转换为压缩的稀疏行表示。

归一化器在sklearn.preprocessing库中对应normalize函数，具体为sklearn.preprocessing.normalize(X, norm='l2', *, axis=1, copy=True, return_norm=False)。其中X是需要规范化的数据，稀疏的矩阵应采用CSR格式；norm用于规格化每个非零采样（或轴为0时每个非零特征）的范数；axis用于规范化数据的轴，如果为1则独立规格化每个样本，否则规格化每个特征；copy设置为False以执行就地行规范化并避免复制；return_norm是否返回计算的归一化值。归一化器也可以使用简化但是等效的Normalizer函数，具体为sklearn.preprocessing.Normalizer(norm='l2', *, copy=True)，其中参数与normalize函数中对应部分一致。

from sklearn.preprocessing import Normalizer
X = [[4, 1, 2, 2], #原始数据
      [1, 3, 9, 3],
      [5, 7, 5, 1]]
transformer = Normalizer().fit(X) #向定标器输入数据，但是无输出
transformer.transform(X) #将原始数据进行归一化
#转化结果是array([[0.8, 0.2, 0.4, 0.4],
#             [0.1, 0.3, 0.9, 0.3],
#             [0.5, 0.7, 0.5, 0.1]])

4. 特征选择

特征选择（Feature selection）：从给定的特征集合中选出相关特征（Feature）子集的过程称为特征选择。在python的经典机器学习库中，sklearn.feature_selection库对应特征选择操作。

首先可以移除相关系数低的特征（Removing features with low variance）。方差或协方差可以用来判断两组数据的相关系数，所以对于两个特征，如果它们的方差为0或者很小，则它们的相关系数很大，即它们包含相同或相似的信息，那么只需留下一个特征就可以保留大部分信息。通过移除相关系数低的特征，减小输入数据的特征数量，降低运算复杂度。实际应用中可以设定一个方差阈值，当特征的方差小于这个阈值就删除该特征，降低总体相似度。在sklearn.feature_selection库中对应VarianceThreshold函数，具体为sklearn.feature_selection.VarianceThreshold(threshold=0.0)，其中threshold表示阈值，即将删除训练集方差低于此阈值的特征。

from sklearn.feature_selection import VarianceThreshold
X = [[0, 2, 0, 3], [0, 1, 4, 3], [0, 1, 1, 3]] #原始数据X
selector = VarianceThreshold() #阈值为0的移除相关系数低的特征选择器
selector.fit_transform(X) #输入数据X，并进行转换（特征选择）
#选择之后的结果   array([[2, 0],
#                     [1, 4],
#                   [1, 1]])

然后对于每个的变量，可以仅对这一个变量进行特征选择，即单变量特征选择（Univariate feature selection）。单变量特征选择法是根据某些统计检验的方法分别对每个变量进行检验，得到一组分数、p-value数据，然后排序选择分数最高(或p-value最小等)的那些特征。单变量特征选择分为两步：第一步先确定如何评分并对所有特征进行评分，第二步根据评分进行排序并选择排序靠前的特征。对于评分，回归问题常用f_regression、mutual_info_regression分数，而分类问题常用f_classif、chi2、mutual_info_classf分数；对于排序和选择，sklearn的feature_selection库提供了SelectKBest、SelectPercentile、SelectFpr和GenericUnivariateSelect。我们这里以SelectKBest为例，这个选择标准就是选取最好的特征，即从所有特征中挑选出最好的K个特征组成新的特征集。而最好的定义就是评分高的，这里以chi2评分为例。SelectKBest函数具体为sklearn.feature_selection.SelectKBest(score_func=, *, k=10)，其中score_func输入评分系统（比如chi2），k表示要选择的特征数量。

from sklearn.datasets import load_digits
from sklearn.feature_selection import SelectKBest, chi2
X, y = load_digits(return_X_y=True) #生成原始数据X和对应的目标值y，进行监督性机器学习
X.shape  #查看原始数据X的大小
#X的数据大小为(1797, 64)，即包含1797*64个数据
X_new = SelectKBest(chi2, k=20).fit_transform(X, y) #向SelectKBest中输入数据并转换，评分选择chi2，选择评分排名前20个特征
X_new.shape #查看选择之后的数据数量
#选择之后的数据X_new只剩(1797, 20)

在机器模型训练的过程中也可以进行特征选择，在每次训练中选择重要的特征留下组成新的数据集（即移除权重比较低的特征），然后用新的数据集进行下一次训练，循环进行直到特征满足要求，这种递归式的特征选择叫做递归特征消除（Recursive feature elimination，简称RFE）。递归特征消除RFE主要分为三步：第一步在特征的初始集合上训练估计器，每个特征的重要性（评分）通过任何特定属性（如coef，feature，importances）或callable获得；第二步将最不重要的特征从当前特征集中剪除，保留下的特征组成新的训练集；第三步重复之前过程在修剪集上递归地重复，直到最终达到所需的要选择的特征数。对于如果确定最后保留的特征数量，可以采用RFECV方法，即交叉验证的递归特征消除，选择最佳数量的特征。递归特征消除在sklearn.feature_selection库中对应RFE函数，具体为sklearn.feature_selection.RFE(estimator, *, n_features_to_select=None, step=1, verbose=0, importance_getter='auto')，其中estimator表示一种有监督的学习估计器，采用拟合方法，提供有关特征重要性的信息（如coef，feature_importances_）；n_features_to_select是要选择的特征数；step如果大于或等于1，则步骤对应于每次迭代中要删除的特征数（整数），如果在（0.0，1.0）之内则步骤对应于在每次迭代中要删除的特征的百分比（向下舍入）；verbose控制输出的详细程度。RFECV对应sklearn.feature_selection库RFECV函数，具体为sklearn.feature_selection.RFECV(estimator, *, step=1, min_features_to_select=1, cv=None, scoring=None, verbose=0, n_jobs=None, importance_getter='auto')，其中min_features_to_select表示要选择的最小功能数，cv确定交叉验证拆分策略，其余参数和RFE相同。

from sklearn.datasets import make_friedman1
from sklearn.feature_selection import RFE
from sklearn.svm import SVR
X, y = make_friedman1(n_samples=50, n_features=10, random_state=0) #生成原始数据集X和目标集y，进行监督性机器学习
estimator = SVR(kernel="linear") #估计器使用SVR，一种基于相关向量机的回归器
selector = RFE(estimator, n_features_to_select=5, step=1) #设置RFE，最终选择五个特征
selector = selector.fit(X, y)
selector.support_ #输出特征的选择结果
#特征的选择结果，false则舍弃该特征 array([ True,  True,  True,  True,  True, False, False, False, False, False])
selector.ranking_ #输出特征的评分排序结果
#特征的评分排序结果 array([1, 1, 1, 1, 1, 6, 4, 3, 2, 5])

除了使用相关系数或评分来消除不重要的特征，也可以使用带惩罚项的基模型用来筛选特征外，而且这个模型同时也进行了降维，进一步减小数据量。常见的带惩罚项的基模型是feature_selection库的SelectFromModel函数，它是结合带L1惩罚项的逻辑回归模型。L1惩罚项降维是通过保留多个对目标值具有同等相关性的特征中的一个特征进行实现的，优点是计算简单，缺点是删除的特征可能包含重要信息。可以结合L2来优化，即当一个特征在L1中的权值1，选择在L2中权值差别不大且在L1中权值为0的特征来构成同类集合。SelectFromModel函数具体为sklearn.feature_selection.SelectFromModel(estimator, *, threshold=None, prefit=False, norm_order=1, max_features=None, importance_getter='auto')，其中estimator是构建变压器的基估计器，threshold是用于特征选择的阈值（重要性大于或等于该值的特征将被保留），max_features是要选择的最大特征数量，prefit表示prefit模型是否希望直接传递到构造函数中；importance_getter决定判断重要性的政策，auto表示使用coef_ 或 feature_importances_，也可以接受一个字符串，该字符串指定用于提取特征重要性的属性名/路径。

from sklearn.feature_selection import SelectFromModel
from sklearn.linear_model import LogisticRegression
X = [[ 0.87, -1.34,  0.31 ], #原始数据集X
      [-2.79, -0.02, -0.85 ],
      [-1.34, -0.48, -2.55 ],
      [ 1.92,  1.48,  0.65 ]]
y = [0, 1, 0, 1] #原始目标集y
selector = SelectFromModel(estimator=LogisticRegression()).fit(X, y) #使用逻辑回归函数作为基本估计器，输入X和y
selector.estimator_.coef_ #输出SelectFromModel的协方差矩阵值（相关系数）
#协方差矩阵是array([[-0.3252302 ,  0.83462377,  0.49750423]])
selector.threshold_ #输出SelectFromModel的阈值
#阈值结果是0.55245...
selector.get_support() #输出SelectFromModel的判断政策
#array([False,  True, False])
selector.transform(X) #对数据集X进行选择
#选择之后的数据集结果是 array([[-1.34],
#                         [-0.02],
#                          [-0.48],
#                          [ 1.48]])

在自然语言处理中，数据是根据时间依次输入的，是时序的。对于这种时序性数据，可以使用顺序（时序）特征选择（Sequential Feature Selection）。时序特征选择是迭代地寻找要添加到所选特征集中的最佳新特征。时序特征选择一般分为前向和后向。前向的时序特征选择过程是从零特征开始，找到一个特征，当一个估计器被训练在这个单一特征上时，它使交叉验证得分最大化；选择了第一个特征之后通过向所选特征集中添加一个新特征来重复这个过程。当达到所需的所选特征数时过程停止。后向的时序特征选择则是从所有特征开始删除。时序特征选择在sklearn.feature_selection库中对应SequentialFeatureSelector函数，具体函数为sklearn.feature_selection.SequentialFeatureSelector(estimator, *, n_features_to_select=None, direction='forward', scoring=None, cv=5, n_jobs=None)。其中direction代表前向或后向，scoring模型评估分数规则，cv确定交叉验证拆分策略，n_jobs表示同时运行的处理器数量，其余参数与之前特征选择函数相同。

from sklearn.feature_selection import SequentialFeatureSelector
from sklearn.neighbors import KNeighborsClassifier
from sklearn.datasets import load_iris
X, y = load_iris(return_X_y=True) #生成原始数据集X和目标集y
knn = KNeighborsClassifier(n_neighbors=3) #使用k近邻方法作为基本估计器
sfs = SequentialFeatureSelector(knn, n_features_to_select=3)
sfs.fit(X, y) #向模型输入数据X和y
#该模型最终参数为SequentialFeatureSelector(estimator=KNeighborsClassifier(n_neighbors=3), n_features_to_select=3)
sfs.get_support()
#选择的策略是array([ True, False,  True,  True])
sfs.transform(X).shape
#选择之后的数据集大小是(150, 3)

5. 主成分分析

进一步进行特征选择，减少要学习的特征（降维），可以使用主成分分析（PCA）选取特征值大的特征向量，给予保留进行下一步学习，这样做的原因是：减轻维数灾难问题；降低学习任务的难度。主成分分析方法是一个经典的机器学习方法，多用于图像降维，具体将在后续经典机器学习方法中介绍。

机器学习一般用于两个领域，图像处理和自然语言处理。在图像处理中可以使用上述介绍的步骤进行预处理。在自然语言处理中，预处理过程主要包括：tokenization，normalization，stemming，stop words。Tokenization预处理将一句话转化为单词，normalization会将字母大小写合并，stemming将同义词干的单词合并，stop words删除无意义单词。这四步预处理的目的也是将训练数据量化（类似于独热编码），然后把输入数据归一化并删除无用数据，方便机器学习或神经网络训练。

1.7 损失函数

我们使用损失函数（loss function）判断模型是否适合。损失函数是估量预测值f(x)和真实值y的不一致程度，即损失函数输入的是真实值y和预测值f(x)，输出一个表示不一致程度的非负数（non-negative）。损失函数可以使用l(y, y’)表示。为了找到模型的最优参数，我们需要使得损失函数值的平均值最小。假设训练集中数据用矩阵X = [x₁,…, x_N]^T,标签用y=[y₁,…, y_N]^T表示，那么损失函数的平均值（也叫empirical risk）是（其中l是损失函数）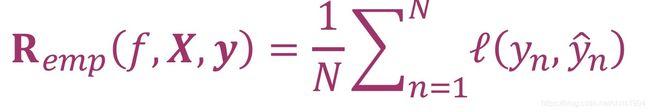
根据不同的机器学习目的和模型应该使用不同的损失函数。因为在特定情况下，有的损失函数可以又更好地收敛性，更不容易产生过拟合等。一般可以根据机器学习是用于分类还是回归，使用不同种类的损失函数。下图中，分别列举了分类和回归情况下常用的损失函数。下面举例说明六种常用的损失函数。

1. 最小平方损失函数

最小平方损失函数（Least-Squares Loss）：也叫均方误差（Mean Square Error，简称MSE），L2 loss。使用真实值和预测值的差的平方求出损失函数，然后再求平均之后的最小值，数学表示为（其中θ为模型的参数）

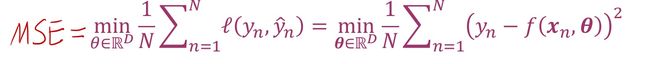
MSE损失函数经常用于回归性机器学习。这不是意味MSE无法用于分类任务，而是效果不好。因为MSE的一个缺点就是其偏导值在输出概率值接近0或者接近1的时候非常小，这可能会造成模型刚开始训练时，偏导值几乎消失。做分类任务时需要使用逻辑回归配合MSE损失函数，当采用梯度下降法进行学习时，会出现模型一开始训练时，学习速率非常慢的情况。所以MSE不适合做分类任务。

在python的机器学习库中，可以使用sklearn.metrics库中的mean_squared_error函数求解MSE。具体为sklearn.metrics.mean_squared_error(y_true, y_pred, *, sample_weight=None, multioutput='uniform_average', squared=True)。其中y_true是真实值，y_pred是预测值，multioutput定义多个输出值的聚合，squared为true时返回MSE否则返回RMSE，RMSE是MSE的开平方值。

from sklearn.metrics import mean_squared_error
y_true = [3, -0.5, 2, 7]
y_pred = [2.5, 0.0, 2, 8]
mean_squared_error(y_true, y_pred)

2. 平均绝对误差损失函数

平均绝对误差损失函数（Mean Absolute Error Loss，简称MAE）：也叫L1 loss，也用在回归问题中。MAE时计算预测值与目标值之间差值的绝对值然后求平均值。MAE 损失的最小值为 0（当预测等于真实值时），最大值为无穷大。随着预测与真实值绝对误差 [y-y‘] 的增加，MAE 损失呈线性增长。

MAE 和 MSE 作为损失函数的主要区别是：MSE 损失相比 MAE 通常可以更快地收敛，但 MAE 损失对于异常值（outliers）更加有鲁棒性，即更加不易受到异常值影响。而且由于MAE 损失与绝对误差之间是线性关系，MSE 损失与误差是平方关系，当误差非常大的时候，MSE 损失会远远大于 MAE 损失。因此当数据中出现一个误差非常大的数据时，MSE 会产生一个非常大的损失，对模型的训练会产生较大的影响。如果训练数据被异常值破坏（即在训练环境中错误地接收到大量不切实际的负值/正值），则MAE是更有效果的。

在python的机器学习库中，可以使用sklearn.metrics库中的mean_absolute_error函数求解MAE。具体为sklearn.metrics.mean_absolute_error(y_true, y_pred, *, sample_weight=None, multioutput='uniform_average')。其中参数与MSE的一致。

from sklearn.metrics import mean_absolute_error
y_true = [3, -0.5, 2, 7]
y_pred = [2.5, 0.0, 2, 8]
mean_absolute_error(y_true, y_pred)

3. 合页损失函数

合页损失函数（Hinge loss）：是二分类损失函数，适用于 maximum-margin 的分类，支持向量机（Support Vector Machine，SVM) 模型。合页损失函数使用真实值的阶跃函数（sgn函数，输入为正时返回1，为负时返回-1）与1比较，然后计算损失。数学表达是（其中z=sgn(y)y’， y是真实值，y’是预测值）

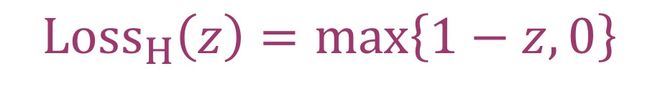
当y 为正类时，模型输出负值会有较大的惩罚，当模型输出为正值且在[0,1] 区间时还会有一个较小的惩罚。即合页损失不仅惩罚预测错的，并且对于预测对了但是置信度不高的也会给一个惩罚，只有置信度高的才会有零损失。所以合页损失函数可以找到一个决策边界，根据边界进行分类。

在python的机器学习库中，可以使用sklearn.metrics库中的hinge_loss函数求解合页损失函数。具体为sklearn.metrics.hinge_loss(y_true, pred_decision, *, labels=None, sample_weight=None)。其中y_true是真实值，pred_decision是预测值，labels用于多分类中的标签。下面代码是多分类问题中合页损失函数的应用。

from sklearn import svm       #调用相关向量机模型
from sklearn.metrics import hinge_loss。#调用hinge loss
import numpy as np   #使用np库建立模拟的数据
X = np.array([[0], [1], [2], [3]])   #输入训练集数据
Y = np.array([0, 1, 2, 3])
labels = np.array([0, 1, 2, 3])  #多分类中的不同类别标签
est = svm.LinearSVC()
est.fit(X, Y)  #学习相关向量机模型
pred_decision = est.decision_function([[-1], [2], [3]])。 #预测值，输入测试集数据
y_true = [0, 2, 3]   #真实值，测试集数据
hinge_loss(y_true, pred_decision, labels=labels)。 #计算多分类中的合页损失函数

4. 0-1损失

0-1损失（Zero-One Loss）：用于二分类问题。当分类正确时loss为0，分类错误时loss为1。数学表达为

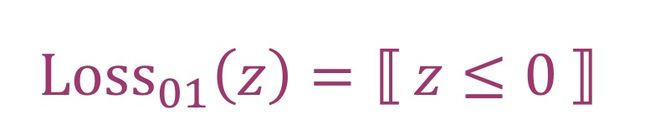
0-1 损失优点是计算简单，但是缺点是对每个错分类点都施以相同的惩罚（损失为 1），这样对犯错比较大的点（ys 远小于 0）无法进行较大的惩罚。而且它是不连续、非凸、不可导，无法使用梯度优化算法。

在python的机器学习库中，可以使用sklearn.metrics库中的zero_one_loss函数求解合页损失函数。具体为sklearn.metrics.zero_one_loss(y_true, y_pred, normalize=True, sample_weight=None)。其中y_true是真实值，y_pred是预测值，normalize（默认值为True）如果为False则返回错误分类的数目，否则返回错误分类的分数。

from sklearn.metrics import zero_one_loss
y_pred = [1, 2, 3, 4]
y_true = [2, 2, 3, 4]
zero_one_loss(y_true, y_pred)   #输出0.25
zero_one_loss(y_true, y_pred, normalize=False)。 #输出1

5. 交叉熵损失函数

交叉熵损失函数（Cross Entropy Loss）：也称负对数似然函数（Log loss），二分类问题中最常用的损失函数。交叉熵损失函数是在概率估计的基础上定义的，它对概率求log然后求负，所以又叫负对数似然函数。它通常用于logistic回归和神经网络，以及评估分类器的概率输出。数学表达式是（其中p=Pr(y=1)，即分类为1的概率，ps二分类总共有1和0两个类；其中y是模型的输出，已经通过使用Sigmoid函数将模型的输出压缩到 (0, 1) 区间内，用来代表模型判断为正类即1的概率。）

熵是一种衡量事件包含的信息量的数据，它可以从h(x)=-log(p(x))求出,p(x)是事件发生的概率。从这个式子还可以得出信息量与概率成反比而且两个独立事件发生的信息量是各自求和。所以二分类的熵是两个类的熵求和，即交叉熵。交叉熵衡量了两个概率分布的差异。其值越大，两个概率分布相差越大；其值越小，则两个概率分布的差异越小。对于分类任务，目的是预测的概率分布与真实的概率分布接近，所以要使得交叉熵最小，即机器学习在二分类任务中在调整参数使得上述交叉熵损失函数最小。

交叉熵损失函数也可以用于多分类任务。在多分类的任务中，真实值是将输出的独热向量使用Softmax函数进行压缩，将每个维度的输出范围都限定在 [0，1] 之间，同时所有维度的输出和为 1。然后对所有分类求它们的交叉熵，再求最小值。

在python的机器学习库中，可以使用sklearn.metrics库中的log_loss函数求解交叉熵损失函数。具体为sklearn.metrics.log_loss(y_true, y_pred, *, eps=1e-15, normalize=True, sample_weight=None, labels=None)。其中y_true是真实值；y_pred是预测值；eps是当交叉熵在p=0和p=1无定义时，概率被剪裁为max(eps，min(1-eps，p))；normalize（默认值为True）为真，则返回每个样本的平均损失，否则返回每个样本损失的总和；label设置标签的由来，默认为y_true。

from sklearn.metrics import log_loss
y_true = [0, 0, 1, 1]
y_pred = [[.9, .1], [.8, .2], [.3, .7], [.01, .99]]
log_loss(y_true, y_pred)

6. 逻辑损失函数

逻辑损失函数（Logistic Loss）：用于解决分类问题中的逻辑回归（Logistic Regression）。 逻辑损失函数本质是交叉熵（cross entropy loss） L = -( y1₁* log(y₁‘) + y₂ * log(y₂’) ) 在 y₁ + y2₂= 1时候的化简。它的数学表达为

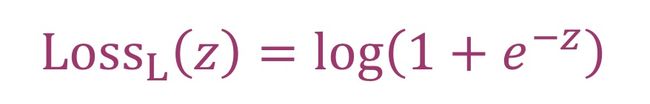
交叉熵用于多分类问题（也可以是二分类），在做k个分类时交叉熵的预测值y‘是一个k维向量。逻辑损失函数用于的逻辑回归本质是时二分类问题，预测值y‘是一个数。所以当k=2时，也就是只有y₁和y₂，它们的概率和为1。在Logistic回归模型使用的Loss函数为Logistic Loss函数，使用极大似然估计法为了使得该Loss函数最小。

下图将这几种常见损失函数的曲线图进行了比较：

1.8 过拟合及其解决办法

当模型在训练集上的正确率很高，但是在测试集上的正确率较低时，可能就出现了过拟合现象（overfitting）。即模型在训练集上数据的特征描述过拟合，模型过训练（overtraining），但是模型缺乏一般性，在其余更广泛的数据上（比如测试集）的预测和回归的正确度较差。在损失函数上体现为，过拟合模型在训练集有较低的误差（error），但是在测试集上有着高的误差。

数据在采集过程中一般带有随机误差（即噪音noise）。这些噪音整体呈正态分布，所以整体上对数据和建模影响不大。但是当模型在训练过程中过于包含每个数据点的所有信息，那么噪音就会对模型的预测产生较大的影响。因为噪音的随机性，也导致了数据之间的噪音会不同。训练集的数据和测试集的数据也会有差异。这些噪音的差异原本是微小的，但是当模型过拟合时将这些噪音的影响放大，测试集和训练集的差异也被放大，这也导致了训练集锁训练的模型不适用于测试集，模型缺乏一般性。如下图所示，左边的回归模型虽然是简单的线性模型，但是表示了正确的回归趋势；右边的模型过于复杂，包含了每个点的噪音，出现了过拟合现象。

过拟合现象一般由过于复杂的模型结构和数据的缺少导致。对于解决过拟合的方法有四种：早停止（early stopping），正则化（regularization），交叉验证和增加数据数量。前两种方法是降低了模型的复杂度，后两种是增加用于训练的数据。对于神经网络还可以通过dropout和减少神经元数量即层次来避免过拟合，这两个方法也是降低模型（神经网络）的复杂度。也可以使用Bagging避免过拟合，即将多个弱学习器Bagging一下效果会好很多（通俗的讲就是分别训练不同的模型，然后让所有模型表决最终的输出结果），Bagging的应用如随机森林。

• 早停止

早停止（early stopping）中会先指定一个验证集（validation_fraction），它是整个数据集的一部分，但是该部分将不进行训练，仅评估模型的验证损失和正确率。使用训练集对模型进行训练，并使用验证集对其进行评估。当每个阶段新的回归模型（回归树regression tree）被训练出来并添加到原模型中时，将使用验证集对模型进行评分。训练持续进行，直到更多的训练迭代却没有改进模型的阶段（n_iter_no_change），这时模型评分没有增加，该模型被认为已经收敛。此时停止添加阶段，进行尽早停止（early stopping）。早停止可以显着减少训练时间，内存使用量和预测延迟。而且早停止可以减少模型复杂度，一定程度上减小过拟合。
早停止可以在sklearn模型的参数中设置，比如下面的梯度下降模型就是加入了早停止，它设置了validation_fraction和n_iter_no_change进行早停止的设定。

gbes = ensemble.GradientBoostingClassifier(n_estimators=n_estimators,
                                               validation_fraction=0.2,
                                               n_iter_no_change=5, tol=0.01,
                                               random_state=0)

• 正则化

正则化一般有三种：L0正则化，L1正则化和L2正则化。L0正则化表示模型参数中非零参数的个数。L1正则化表示各个参数绝对值之和。L2正则化表示各个参数的平方的和的开方值。以最小方差做损失函数为例，在最小方差后面加上一项变成了下式

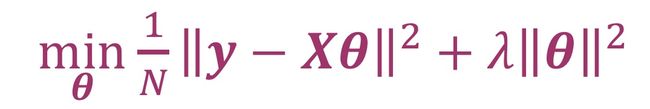
新添加的项就是正则化项（regularizer），也叫惩罚项（penalty term）。系数λ叫做正则化系数（regularization parameter）。λ可以在最小化训练集的损失函数和参数θ的之间进行调整。如果发生过拟合，θ参数的大小会变得相对较大，也就是加大λ。而且λ是超参数，需要人为在训练前设置。

L0正则化通过添加L0范数（即非零参数的个数）使得参数变得稀疏化，减小模型的复杂度，从而避免过拟合。但是L0的求解过程复杂，是个NP难问题，所以可以采用L1正则化代替L0正则化。L1正则化是L0正则化的最优凸近似，计算更加简单。

L1正则化的回归模型也称为Lasso回归（Lasso Regression），它的损失函数是（黄色部分是L1的惩罚项）：

Lasso回归（全称是最小绝对收缩和选择算子，Least Absolute Shrinkage and Selection Operator）将系数的“幅度绝对值”作为损失项的惩罚项。如果lambda为零，那么模型回到了OLS。但是，如果lambda很大，则会增加过多的惩罚，会导致拟合不足即欠拟合。Lasso回归将次要特征的系数缩小为零，从而完全删除了某些特征。与L0正则化类似，L1正则化也可以产生更稀疏的权值矩阵。所以Lasso回归适用于功能选择（feature selection），同时一定程度上防止过拟合。而且L1正则化适用于特征之间有关联的情况。

Lasso回归在python的机器学习库sklearn中对应sklearn.linear_model.Lasso函数。具体为sklearn.linear_model.Lasso(alpha=1.0, *, fit_intercept=True, normalize=False, precompute=False, copy_X=True, max_iter=1000, tol=0.0001, warm_start=False, positive=False, random_state=None, selection='cyclic')，其中alpha是与L1项相乘的常数，默认为1.0；fit_intercept是否计算此模型的截距，false代表不计算即数据居中；normalize如果为True，则将在回归之前通过减去均值并除以l2-范数来对回归变量X进行归一化；precompute代表是否使用预先计算的Gram矩阵来加快计算速度；max_iter代表最大迭代次数；random_state选择随机特征进行更新的伪随机数生成器的种子。具体应用如下：

from sklearn import linear_model
clf = linear_model.Lasso(alpha=0.1)
clf.fit([[0,0], [1, 1], [2, 2]], [0, 1, 2])
#训练模型Lasso(alpha=0.1)
print(clf.coef_)
#结果是[0.85 0.  ]
print(clf.intercept_)
#结果是0.15...
#可以使用clf.predict(X)进行预测

L2正则化的回归模型也称为Ridge回归（Ridge Regression），它的损失函数是（黄色部分是L2的惩罚项）：

Ridge回归（也叫岭回归）将系数的“平方大小”作为损失项添加到损失函数中。如果lambda为零，那么模型回到了OLS。但是，如果lambda很大，则会增加过多的惩罚，会导致拟合不足即欠拟合。Ridge回归适用于数据中存在共线性的情况(非满秩矩阵)。而且Lasso回归系数beta可以缩减到0，Ridge回归的beta不可以为0。L2正则化主要用于防止模型过拟合。而且L2正则化适用于特征之间没有关联的情况。

Ridge回归在python的机器学习库sklearn中对应sklearn.linear_model.Ridge函数。具体为sklearn.linear_model.Ridge(alpha=1.0, *, fit_intercept=True, normalize=False, copy_X=True, max_iter=None, tol=0.001, solver='auto', random_state=None)，其中参数与Lasso回归模型中对应参数意义相同。具体应用如下：

from sklearn.linear_model import Ridge
import numpy as np
n_samples, n_features = 10, 5
rng = np.random.RandomState(0)
y = rng.randn(n_samples)
X = rng.randn(n_samples, n_features)
clf = Ridge(alpha=1.0)
clf.fit(X, y)   #生成Ridge()模型
#可以使用clf.predict(X)进行预测

• 交叉验证

使用交叉验证在训练中实时对模型进行检测，选择效果最好的模型。交叉验证其实是对训练集数据的循环应用，当训练数据较少时采用，但是训练数据足够多时则没有必要。交叉验证的具体实现见1.5节的k折交叉验证。

• 增加数据数量

增加更多数据进行训练是最好的减少过拟合的方法，但是一般情况下数据的采取比较困难（尤其是带label的数据），这个方法也是最难实现的。增加更多数据的方法有：1. 从数据源头采集更多数据；2. 复制原有数据并加上随机噪声； 3. 重采样； 4. 根据当前数据集估计数据分布参数，使用该分布产生更多数据。

2 机器学习主要步骤

机器学习主要有五步：

1. 数据采集或生成
2. 数据预处理
3. 机器学习模型选择，调整参数
4. 模型训练和验证
5. 模型测试并选择最终模型

下图展示了从问题的定义到最后生成模型的步骤。

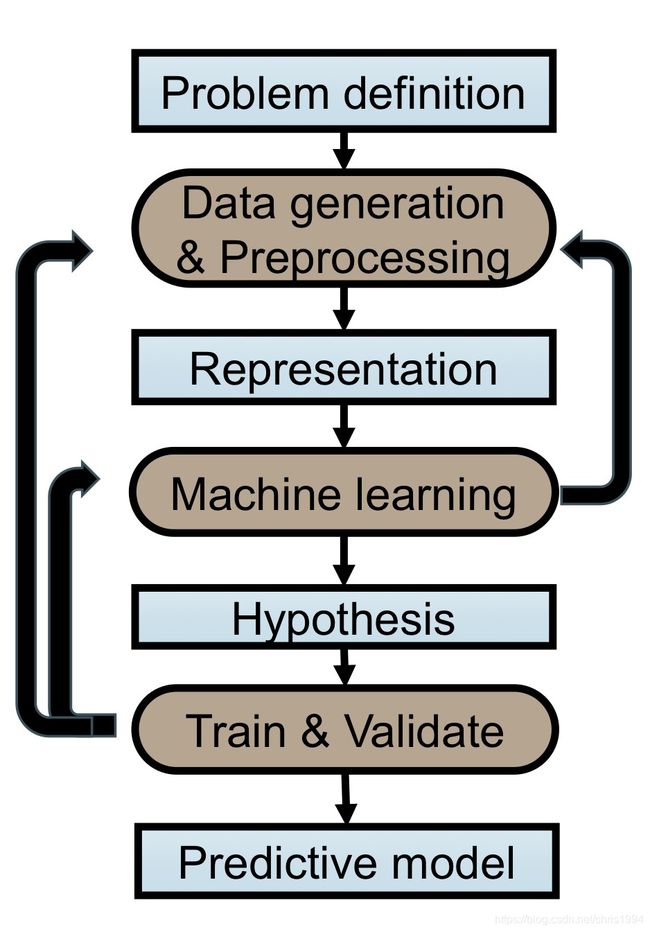
从图可以看出，机器学习的第一步就是数据的采集和生成。这些数据通过实验或者调查得到，有的在经过人为加工（贴标签）后成为带标签的数据。数据中可能有噪音和一些无用数据。下一步就是对数据进行预处理，将非数字数据进行独热编码，将其变成数据性向量，便于计算。对无用数据进行删除，对缺失数据进行填补，对量级过大的数据或量级过小的数据通过标准化和归一化处理。然后要分析问题，判断机器学习的类型，是有监督学习还是无监督学习，是预测还是回归，是分类还是聚簇。然后根据机器学习类型选择合适的机器学习方法。比如若是回归问题可以使用线性回归，lasso回归或ridge回归。若是分类问题则选择k近邻或基于支持向量机的分类。若是聚簇问题可以使用kmeans。下图是sklearn库中给出的根据数据的类型进行机器学习种类的判断，图中根据数据的大小，有无标签或其他条件一步步分析使用不同的机器学习方法。

选择完机器学习方法之后就需要建模，一般可以直接使用sklearn中的模型函数，也可以使用pytorch等搭建神经网络。建模中最重要的就是参数的选择，尤其是超参数的选取。同样的模型，不同的参数，导致的结果也会千变万化。比如kmeans中使用几个中心点和中心点的生成。可以通过分析数据确定其中参数，也可以通过多次尝试不同参数训练选择最佳（超参数一般都要多次尝试）。模型选择这个阶段可能会对问题又进一步的认识，可能发现有些特征不是模型需要的，也有可能有些缺省值的填补会影响模型（比如0）。如果是有监督学习，还要选择某一个特征作为目标值。这时就要重回数据预处理过程，对数据进行再次的特征选择和缺省值填补。在进行训练之前，还有将数据分成训练集和测试集，有时也要有验证集（不是必须）。如果数据的数量过少，可以使用交叉验证。然后要选择合适的损失函数。根据机器学习的种类选择合适的损失函数，也可以尝试不同损失函数的训练效果，再进行选择。接下来就可以进行模型的训练和验证了。设定好训练的次数，训练误差的阈值，选择是否使用梯度下降等，开始训练（真正的机器学习）。模型的大部分参数都会在训练中计算机根据数据进行学习得到。使用训练集对已经搭建好的模型（假设）进行训练，使用验证集选择效果最好的模型，使用测试集对模型进行评估。此时如果测试集的评估效果不好，正确率过低，可能要对模型进行调整。当发送过拟合时，要在模型中加入正则化，在训练中设置早停止，如果是神经网络则要在训练中加入dropout。模型的调整根据问题和数据而定。评估效果不好可能不是过拟合，而是模型选择的问题。当线性回归或者lasso回归等的效果不好时，可以使用SVR或者直接该换成神经网络（神经网络是在线性神经元的基础上加上激励函数，更加适用非线性问题）。当线性分类效果不好，使用SVM（支持向量机），使用超平面代替单一分界线。当kmeans的效果不好时可以使用高斯混合模型（GMM），GMM适用解决数据由多个高斯分布组成，也可以使用EM算法（kmeans和GMM都是基于EM算法实现的）进行其他模型的建立。在调整完模型，进行了新的假设，之后继续训练和评估，直到模型效果达到要求。最后生成学习好的模型，使用这个模型进行之后的预测或者其他问题研究（sklearn库中的模型函数一般带有predict()函数用于预测数据）。