数据结构与算法之美
数据结构与算法之美
- 概念
- 数据结构
- 指一组数据的存储结构
- 图书馆储藏书籍,为了方便查找,一般会将书籍分门别类进行“存储”;按照一定规律编号,就是书籍这种“数据”的存储结构
- 算法
- 操作数据的一组方法
- 那如何来查找一本书呢?有很多种办法,你当然可以一本一本地找,也可以先根据书籍类别的编号,是人文,还是科学、计算机,来定位书架,然后再依次查找;笼统地说,这些查找方法都是算法
- 数据结构是为算法服务的,算法要作用在特定的数据结构之上
- 数据结构
- roadMap
- 脑图

- 复杂度分析
- 时间复杂度
- 最好、最坏、平均、均摊
- 空间复杂度
- 时间复杂度
- 数据结构
- 线性表
- 数组
- 链表
- 单链表
- 双向链表
- 循环链表
- 双向循环链表
- 静态链表
- 栈
- 顺序栈
- 链式栈
- 队列
- 普通队列
- 双端队列
- 阻塞队列
- 并发队列
- 阻塞并发队列
- 散列表
- 散列函数
- 冲突解决
- 链表法
- 开放寻址
- 其他
- 动态扩容
- 位图
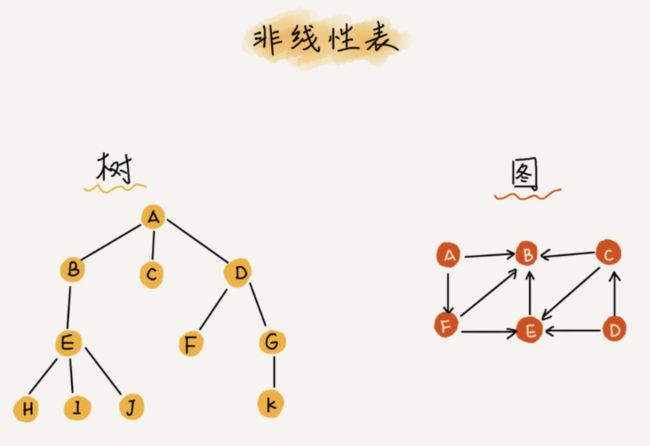
- 树
- 二叉树
- 平衡二叉树
- 二叉查找树
- 平衡二叉查找树
- AVL树
- 红黑树
- 完全二叉树
- 满二叉树
- 多路查找树
- B树
- B+树
- 2-3树
- 2-3-4树
- 堆
- 小顶堆
- 大顶堆
- 优先级队列
- 斐波那契堆
- 二项堆
- 其他
- 树状数组
- 线段树
- 二叉树
- 图
- 图的存储
- 邻接矩阵
- 邻接表
- 拓扑排序
- 最短路径
- 关键路径
- 最小生成树
- 二分图
- 最大流
- 图的存储
- 线性表
- 算法
- 基本算法思想
- 贪心算法
- 分治算法
- 动态规划
- 回溯算法
- 枚举算法
- 排序
- O(n^2)
- 冒泡排序
- 插入排序
- 选择排序
- 希尔排序
- O(nlogn)
- 归并排序
- 快速排序
- 堆排序
- O(n)
- 计数排序
- 基数排序
- 桶排序
- O(n^2)
- 搜索
- 深度优先查找
- 广度优先查找
- A*启发式搜索
- 查找
- 线性表查找
- 树结构查找
- 散列表查找
- 字符串匹配
- 朴素
- KMP
- Robin-Karp
- Boyer-Moore
- AC自动机
- Trie
- 后缀数组
- 其他
- 数论
- 计算几何
- 概率分析
- 并查集
- 拓扑网络
- 矩阵运算
- 线性规划
- 基本算法思想
- 脑图
- 常见数据结构
- 数组(Array)
- 一种线性表数据结构,用一组连续的内存空间,来存储一组具有相同类型的数据
- 数组和链表的区别
- 链表适合插入、删除,时间复杂度 O(1)
- 数组适合查找,支持随机访问,根据下标随机访问的时间复杂度为 O(1)
- 数组查找的时间复杂度并不为 O(1),即便是排好序的数组,用二分查找,时间复杂度也是 O(logn)
- 低效的“插入”和“删除”
- 插入(O(n))
- 有序的
- 最好O(1),最坏O(n),平均O(n)
- 无序的
- O(1)
- 数组中存储的数据并没有任何规律,数组只是被当作一个存储数据的集合
- 直接将第 k 位的数据搬移到数组元素的最后,把新的元素直接放入第 k 个位置
- 时间复杂度就会降为 O(1)
- 有序的
- 删除(O(n))
- 最好O(1),最坏O(n),平均O(n)
- 在某些特殊场景下,我们并不一定非得追求数组中数据的连续性,如果我们将多次删除操作集中在一起执行,删除的效率是会提高很多(垃圾桶)
- 每次的删除操作并不是真正地搬移数据,只是记录数据已经被删除
- 当数组没有更多空间存储数据时,我们再触发执行一次真正的删除操作,这样就大大减少了删除操作导致的数据搬移
- JVM 标记清除垃圾回收算法的核心思想
- 插入(O(n))
- 数组访问越界
- 在 C 语言中,只要不是访问受限的内存,所有的内存空间都是可以自由访问的
- 数组越界一般都会出现莫名其妙的逻辑错误
- 不是所有语言都和C一样,Java 、Python等会自己做越界检查,不需要程序员来做
- 容器能否完全替代数组?
- 针对数组类型,很多语言都提供了容器类,比如 Java 中的 ArrayList、C++ STL 中的 vector
- ArrayList 最大的优势就是可以将很多数组操作的细节封装起来、支持动态扩容
- 更适合用数组情况
- Java ArrayList 无法存储基本类型,比如 int、long,需要封装为 Integer、Long 类,而 Autoboxing、Unboxing 则有一定的性能消耗,所以如果特别关注性能,或者希望使用基本类型,就可以选用数组
- 如果数据大小事先已知,并且对数据的操作非常简单,用不到 ArrayList 提供的大部分方法,也可以直接使用数组
- 当要表示多维数组时,用数组往往会更加直观。比如 Object[][] array;而用容器的话则需要这样定义:ArrayList array
- 为什么大多数编程语言中,数组要从 0 开始编号,而不是从 1 开始呢?
- 从0开始编号,计算 a[k] 的内存地址:
a[k]_address = base_address + k * type_size - 从1开始编号,计算 a[k] 的内存地址:
a[k]_address = base_address + (k-1) * type_size - 每次随机访问数组元素都多了一次减法运算,对于 CPU 来说,就是多了一次减法指令
- 另外一个历史原因,C 语言设计者用 0 开始计数数组下标,之后的 Java、JavaScript 等高级语言都效仿了 C 语言
- 从0开始编号,计算 a[k] 的内存地址:
- 链表(Linked list)
- 应用场景
- 缓存
- 一种提高数据读取性能的技术,有着非常广泛的应用,比如常见的 CPU 缓存、数据库缓存、浏览器缓存
- 缓存的大小有限,当缓存被用满时,哪些数据应该被清理出去,哪些数据应该被保留?
- 缓存淘汰策略
- 先进先出策略 FIFO(First In,First Out)
- 最少使用策略 LFU(Least Frequently Used)
- 最近最少使用策略 LRU(Least Recently Used)
- 缓存淘汰策略
- 缓存
- 应用场景
- 栈
- 队列
- 散列表
- 二叉树
- 堆
- 跳表
- 图
- Trie 树
- 数组(Array)
- 常见算法
- 递归
- 排序
- 二分查找
- 搜索
- 哈希算法
- 贪心算法
- 分治算法
- 回溯算法
- 动态规划
- 字符串匹配算法
- 技巧
- 每种数据结构和算法,要学习它的“来历”“自身的特点”“适合解决的问题”以及“实际的应用场景”
- 边学边练,适度刷题
- 建议每周花 1~2 个小时的时间,集中把这周的三节内容涉及的数据结构和算法,全都自己写出来,用代码实现一遍
- 可以“适度”刷题,但一定不要浪费太多时间在刷题上,学习的目的还是掌握,然后应用
- 多问、多思考、多互动
- 学习最好的方法是,找到几个人一起学习,一块儿讨论切磋,有问题及时寻求老师答疑
- 打怪升级学习法
- 学习的过程中,我们碰到最大的问题就是,坚持不下来
- 为什么很多看起来非常简单又没有乐趣的游戏,会玩得不亦乐乎呢?这是因为,当你努力打到一定级别之后,每天看着自己的经验值、战斗力在慢慢提高,那种每天都在一点一点成长的成就感就不由自主地产生了
- 所以,我们在枯燥的学习过程中,也可以给自己设立一个切实可行的目标,就像打怪升级一样
- 每节课后都写一篇学习笔记或者学习心得,发布到平台,让大家点赞评论,激励自己
- 如果你能这样学习一段时间,不仅能收获到知识,你还会有意想不到的成就感,因为,这其实帮你改掉了一点学习的坏习惯
- 知识需要沉淀,不要想试图一下子掌握所有
- 学习知识的过程是反复迭代、不断沉淀的过程
- 想听一遍、看一遍就把所有知识掌握,这肯定是不可能的
- 碰到“拦路虎”,可以先沉淀一下,过几天再重新学一遍
- 书读百遍其义自见
- FLAG
- 所有数据结构与算法用Python实现一遍
- 所有数据结构与算法用Java实现一遍
- 学完就辞职
- 复杂度分析
-
数据结构和算法本身解决的是“快”和“省”的问题,即如何让代码运行得更快,如何让代码更省存储空间
-
执行效率是算法一个非常重要的考量指标
-
复杂度分析是整个算法学习的精髓,只要掌握了它,数据结构和算法的内容基本上就掌握了一半
-
事后统计法
- 把代码跑一遍,通过统计、监控,就能得到算法执行的时间和占用的内存大小
- 局限性
- 测试结果非常依赖测试环境
- 测试环境中硬件的不同会对测试结果有很大的影响
- 测试结果受数据规模的影响很大
- 测试结果非常依赖测试环境
-
大 O 复杂度表示法
- 一个不用具体的测试数据来测试,就可以粗略地估计算法的执行效率的方法
int cal(int n) { int sum = 0; # 1 个 unit_time int i = 1; # 1 个 unit_time int j = 1; # 1 个 unit_time for (; i <= n; ++i) { # n 个 unit_time j = 1; # n 个 unit_time for (; j <= n; ++j) { # n*n 个 unit_time sum = sum + i * j; # n*n 个 unit_time } } } # 执行时间 T(n) = (2n^2+2n+3) * unit_time # T(n) = O(2n^2+2n+3) # T(n) = O(n^2)- 从 CPU 的角度来看,每一行都执行着类似的操作:读数据-运算-写数据
- 假设每行代码执行的时间都一样,为 unit_time
- 所有代码的执行时间 T(n) 与每行代码的执行次数成正比
- T ( n ) = O ( f ( n ) ) T(n)=O(f(n)) T(n)=O(f(n))
- T(n) ——代码执行的时间
- n ——数据规模的大小
- f(n) ——每行代码执行的次数总和
- O——代码的执行时间 T(n) 与 f(n) 表达式成正比
- 公式中的低阶、常量、系数三部分并不左右增长趋势,所以都可以忽略。我们只需要记录一个最大量级就可以
- 上面的例子最终可以表示为 ‘ T ( n ) = O ( n 2 ) ‘ `T(n)=O(n^2)` ‘T(n)=O(n2)‘
- T ( n ) = O ( f ( n ) ) T(n)=O(f(n)) T(n)=O(f(n))
-
时间复杂度分析
-
渐进时间复杂度(asymptotic time complexity),简称时间复杂度
-
表示算法的执行时间与数据规模之间的增长关系,并不具体表示代码真正的执行时间
-
分析方法
-
只关注循环执行次数最多的一段代码
-
加法法则:总复杂度等于量级最大的那段代码的复杂度
int cal(int n) { int sum_1 = 0; int p = 1; for (; p < 100; ++p) { sum_1 = sum_1 + p; } int sum_2 = 0; int q = 1; for (; q < n; ++q) { sum_2 = sum_2 + q; } int sum_3 = 0; int i = 1; int j = 1; for (; i <= n; ++i) { j = 1; for (; j <= n; ++j) { sum_3 = sum_3 + i * j; } } return sum_1 + sum_2 + sum_3; # 100 + n + n^2 } # O(n^2) -
乘法法则:嵌套代码的复杂度等于嵌套内外代码复杂度的乘积
int cal(int n) { int ret = 0; int i = 1; for (; i < n; ++i) { ret = ret + f(i); } } int f(int n) { int sum = 0; int i = 1; for (; i < n; ++i) { sum = sum + i; } return sum; } # T(n) = T1(n) * T2(n) = O(n*n) = O(n^2)
-
-
几种常见时间复杂度实例分析
- 多项式量级
-
常数阶O(1)
int i = 8; int j = 6; int sum = i + j; # T(n)=O(1), T(n)!=O(3)- 只是常量级时间复杂度的一种表示方法,并不是指只执行了一行代码
- 只要代码的执行时间不随 n 的增大而增长,这样代码的时间复杂度我们都记作 O(1)
- 一般情况下,只要算法中不存在循环语句、递归语句,即使有成千上万行的代码,其时间复杂度也是Ο(1)
-
对数阶O(logn)、线性对数阶O(nlogn)
i=1; while (i <= n) { i = i * 2; } # T(n)=O(log2n) ==> T(n)=O(logn) i=1; while (i <= n) { i = i * 3; } # T(n)=O(log3n) ==> T(n)=O(logn)- 在对数阶时间复杂度的表示方法里,我们忽略对数的“底”,统一表示为 O(logn)
- O ( l o g 3 n ) = O ( l o g 3 2 ∗ l o g 2 n ) = O ( l o g 3 2 ) ∗ O ( l o g 2 n ) = O ( l o g 2 n ) O(log_{3}n) = O(log_{3}2*log_{2}n)=O(log_{3}2)*O(log_{2}n)=O(log_{2}n) O(log3n)=O(log32∗log2n)=O(log32)∗O(log2n)=O(log2n)
- 如果一段代码的时间复杂度是 O(logn),我们循环执行 n 遍,时间复杂度就是 O(nlogn) 了(乘法法则)
- 在对数阶时间复杂度的表示方法里,我们忽略对数的“底”,统一表示为 O(logn)
-
线性阶O(n)
int cal(int m, int n) { int sum_1 = 0; int i = 1; for (; i < m; ++i) { sum_1 = sum_1 + i; } int sum_2 = 0; int j = 1; for (; j < n; ++j) { sum_2 = sum_2 + j; } return sum_1 + sum_2; } # T(n) = O(m+n) # 无法事先评估 m 和 n 谁的量级大 -
平方阶O(n2)、立方阶O(n3)、……、k次方阶O(n^k)
-
- 非多项式量级
- 指数阶O(2^n)
- 阶乘阶O(n!)
- 当 n 越来越大时,非多项式量级算法的执行时间会急剧增加,是非常低效的算法
- 多项式量级
-
-
空间复杂度分析
- 渐进空间复杂度(asymptotic space complexity),简称空间复杂度
- 表示算法的存储空间与数据规模之间的增长关系
void print(int n) { int i = 0; int[] a = new int[n]; # n unit_space for (i; i <n; ++i) { a[i] = i * i; } for (i = n-1; i >= 0; --i) { print out a[i] } } # S(n)=O(n)- 常见的空间复杂度就是 O(1)、O(n)、O(n^2 ),像 O(logn)、O(nlogn) 这样的对数阶复杂度平时都用不到
- 空间复杂度分析比时间复杂度分析要简单很多
-
最好情况时间复杂度(best case time complexity)、最坏情况时间复杂度(worst case time complexity)、平均情况时间复杂度(average case time complexity)
- 最好情况时间复杂度就是,在最理想的情况下,执行这段代码的时间复杂度
- 最坏情况时间复杂度就是,在最糟糕的情况下,执行这段代码的时间复杂度
- 平均时间复杂度的全称应该叫加权平均时间复杂度或者期望时间复杂度
// n 表示数组 array 的长度 int find(int[] array, int n, int x) { int i = 0; int pos = -1; for (; i < n; ++i) { if (array[i] == x) pos = i; } return pos; } # T(n)=O(n) // n 表示数组 array 的长度 int find(int[] array, int n, int x) { int i = 0; int pos = -1; for (; i < n; ++i) { if (array[i] == x) { pos = i; break; } } return pos; } # 最好情况时间复杂度 O(1) # 最坏情况时间复杂度 O(n) # 平均情况时间复杂度 O(n)- 要查找的变量 x 在数组中的位置,有 n+1 种情况:在数组的 0~n-1 位置中和不在数组中。我们把每种情况下,查找需要遍历的元素个数累加起来,然后再除以 n+1,就可以得到需要遍历的元素个数的平均值
- T ( n ) = O ( 1 + 2 + 3 + . . . + n + n n + 1 ) = O ( n ( n + 3 ) 2 ( n + 1 ) ) = O ( n ) T(n)=O(\frac{1+2+3+...+n+n}{n+1})=O(\frac{n(n+3)}{2(n+1)})=O(n) T(n)=O(n+11+2+3+...+n+n)=O(2(n+1)n(n+3))=O(n)
- 考虑概率,要查找的变量 x,要么在数组里,要么就不在数组里。这两种情况对应的概率统计起来很麻烦,为了方便你理解,我们假设在数组中与不在数组中的概率都为 1/2。另外,要查找的数据出现在 0~n-1 这 n 个位置的概率也是一样的,为 1/n。所以,根据概率乘法法则,要查找的数据出现在 0~n-1 中任意位置的概率就是 1/(2n)
- T ( n ) = O ( 1 ∗ 1 2 n + 2 ∗ 1 2 n + 3 ∗ 1 2 n + . . . + n ∗ 1 2 n + n ∗ 1 2 ) = O ( 3 n + 1 4 ) = O ( n ) T(n)=O(1*\frac{1}{2n}+2*\frac{1}{2n}+3*\frac{1}{2n}+...+n*\frac{1}{2n}+n*\frac{1}{2})=O(\frac{3n+1}{4})=O(n) T(n)=O(1∗2n1+2∗2n1+3∗2n1+...+n∗2n1+n∗21)=O(43n+1)=O(n)
-
均摊时间复杂度(amortized time complexity)
// array 表示一个长度为 n 的数组 // 代码中的 array.length 就等于 n int[] array = new int[n]; int count = 0; void insert(int val) { if (count == array.length) { int sum = 0; for (int i = 0; i < array.length; ++i) { sum = sum + array[i]; } array[0] = sum; count = 1; } array[count] = val; ++count; } # 这段代码实现了一个往数组中插入数据的功能。当数组满了之后,也就是代码中的 count == array.length 时, # 我们用 for 循环遍历数组求和,并清空数组,将求和之后的 sum 值放到数组的第一个位置,然后再将新的数据插入。 # 但如果数组一开始就有空闲空间,则直接将数据插入数组 # 最理想的情况下,数组中有空闲空间,我们只需要将数据插入到数组下标为 count 的位置就可以了,所以最好情况时间复杂度为 O(1) # 最坏的情况下,数组中没有空闲空间了,我们需要先做一次数组的遍历求和,然后再将数据插入,所以最坏情况时间复杂度为 O(n) # 平均时间复杂度:O(1) # 假设数组的长度是 n,根据数据插入的位置的不同,我们可以分为 n 种情况,每种情况的时间复杂度是 O(1)。 # 除此之外,还有一种“额外”的情况,就是在数组没有空闲空间时插入一个数据,这个时候的时间复杂度是 O(n)。 # 而且,这 n+1 种情况发生的概率一样,都是 1/(n+1) # 1*1/(n+1) + 1*1/(n+1) + ... + 1*1/(n+1) + n*1/(n+1) = O(1) # 均摊时间复杂度:O(1) # insert() 在大部分情况下,时间复杂度都为 O(1) # O(1)时间复杂度的插入和 O(n) 时间复杂度的插入,出现的频率是非常有规律的 # 而且有一定的前后时序关系,一般都是一个 O(n) 插入之后,紧跟着 n-1 个 O(1) 的插入操作,循环往复 # 每一次 O(n) 的插入操作,都会跟着 n-1 次 O(1) 的插入操作,所以把耗时多的那次操作均摊到接下来的 n-1 次耗时少的操作上, # 均摊下来,这一组连续的操作的均摊时间复杂度就是 O(1) // 全局变量,大小为 10 的数组 array,长度 len,下标 i。 int array[] = new int[10]; int len = 10; int i = 0; // 往数组中添加一个元素 void add(int element) { if (i >= len) { // 数组空间不够了 // 重新申请一个 2 倍大小的数组空间 int new_array[] = new int[len*2]; // 把原来 array 数组中的数据依次 copy 到 new_array for (int j = 0; j < len; ++j) { new_array[j] = array[j]; } // new_array 复制给 array,array 现在大小就是 2 倍 len 了 array = new_array; len = 2 * len; } // 将 element 放到下标为 i 的位置,下标 i 加一 array[i] = element; ++i; } # 最好是O(1),最差是O(n), 平均均摊是O(1)- 均摊时间复杂度就是一种特殊的平均时间复杂度
- 均摊时间复杂度和摊还分析应用场景比较特殊
- 对一个数据结构进行一组连续操作中,大部分情况下时间复杂度都很低,只有个别情况下时间复杂度比较高,而且这些操作之间存在前后连贯的时序关系,这个时候,我们就可以将这一组操作放在一块儿分析,看是否能将较高时间复杂度那次操作的耗时,平摊到其他那些时间复杂度比较低的操作上。而且,在能够应用均摊时间复杂度分析的场合,一般均摊时间复杂度就等于最好情况时间复杂度
-