使用MATLAB进行数据分析 - Matlab数据分析方法 - 插值与拟合

1 数据插值

一般地，从各种试验得来的数据总是有一定的数量，而利用插值技术能够从有限的数据中获取系统整体的状态，因此，数据插值在各行各业，特别是信号处理领域内有着广泛的应用。

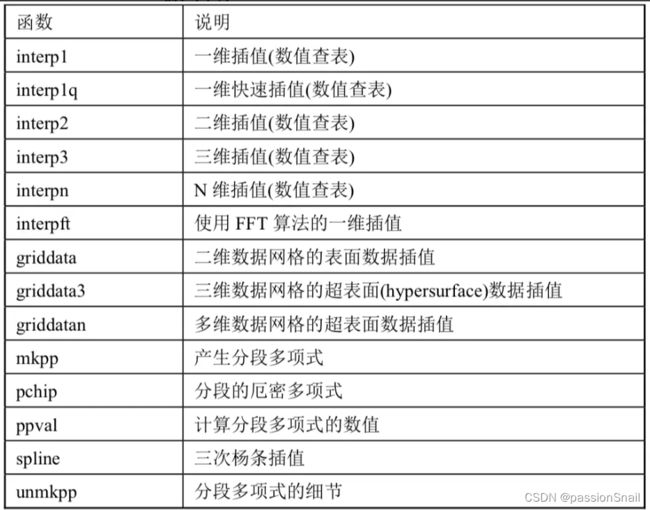
常用数据插值函数如下：

函数中较常用的就是进行基本插值的 interp 系列函数，其中 interp1 和 interp1q 函数比较起来，后者在处理 X 为单调递增的向量，Y 为列向量或者行数同 X 向量长度的矩阵进行插值计算的时候，速度较快，而且仅能进行线性插值。

interp1 函数一般的用法为 yi = interp1(x, y, xi, method)

其中:

• x 和 y 为原始数据，xi 为需要计算的插值点。method 可以为插值计算指定相应的算法，为字符串类型，其取值可以为 nearestlinearsplinecubicpchipv5cubic。

若进行插值运算时，xi 的取值超过了 x 的范围，则需要进行外插运算，这个时候需要在使用函数的时候指定参数 extrap，即函数的使用方法为yi = interp1(x, y, xi, method, 'extrap')

插值方法	说明
'linear'	线性插值。这是默认的插值方法
'nearest'	最近邻居插值
'next'	下一个邻居插值
'previous'	先前的邻居插值
'pchip'	保形分段三次插值
'cubic'	和'pchip'一样
'v5cubic'	在MATLAB使用三次卷积
'makima'	修改的Akima立方Hermite插值
'spline'	使用无结节结束条件的样条插值

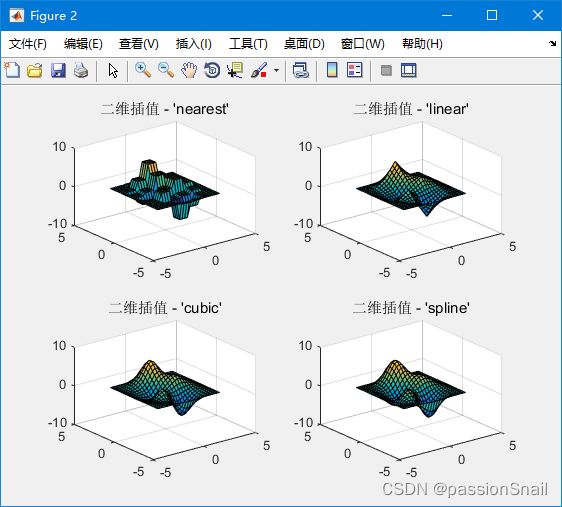
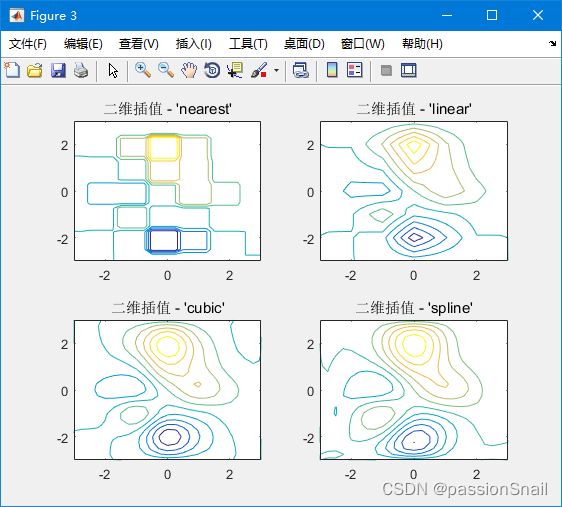
二维插值运算函数的使用方法类似一维插值运算函数的使用方法，同样也可以在使用函数的同时指定相应的算法：nearestlinearcubicspline 等。与一维插值不同的是，这里使用的插值算法都需要进行双次运算，所以也可以在算法选择时使用 bilinear 或者bicubic关键字指定相应的算法。在例子中，对这几种插值算法进行了比较，并用 contour 进行了可视化处理：

close all
clear
clc

%% COMPARE_INTERP 不同插值运算的比较
% 原始数据
[x,y]=meshgrid(-3:1:3);
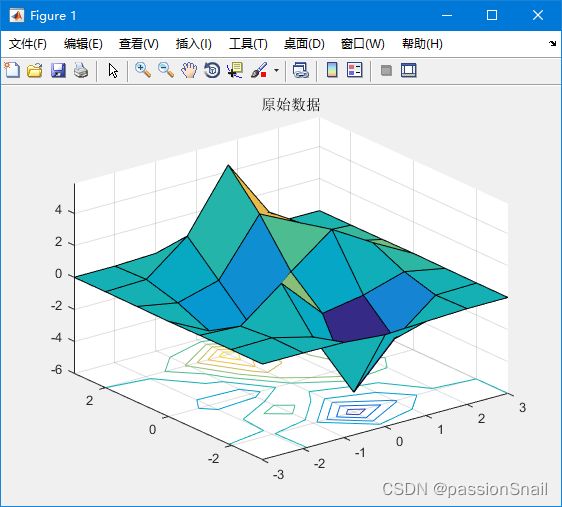
z =peaks(x,y);figure(1); clf
surfc(x,y,z);title('原始数据')% 进行插值运算
[xi, yi]=meshgrid(-3:0.25:3);

zi1 =interp2(x,y,z,xi,yi,'nearest');
zi2 =interp2(x,y,z,xi,yi,'linear');
zi3 =interp2(x,y,z,xi,yi,'cubic');
zi4 =interp2(x,y,z,xi,yi,'spline');% 通过可视化结果比较

figure(2)
subplot(2,2,1);surf(xi,yi,zi1);title('二维插值 - ''nearest''')
subplot(2,2,2);surf(xi,yi,zi2);title('二维插值 - ''linear''')
subplot(2,2,3);surf(xi,yi,zi3);title('二维插值 - ''cubic''')
subplot(2,2,4);surf(xi,yi,zi4);title('二维插值 - ''spline''')% 可视化结果

figure(3)
subplot(2,2,1);contour(xi,yi,zi1);title('二维插值 - ''nearest''')
subplot(2,2,2);contour(xi,yi,zi2);title('二维插值 - ''linear''')
subplot(2,2,3);contour(xi,yi,zi3);title('二维插值 - ''cubic''')
subplot(2,2,4);contour(xi,yi,zi4);title('二维插值 - ''spline''')

2 曲线拟合

回归分析是曲线拟合的常用方法，最小二乘法是回归分析法的一种方法。

回归分析法曲线拟合：

close all
clear
clc

%%
t = [0 .3 .8 1.1 1.6 2.3]';
y = [0.5 0.82 1.14 1.25 1.35 1.40]';
plot(t,y,'r*')
grid on

%%
X = [ones(size(t))  t  t.^2];
A = X\y;
T = (0:0.1:2.5)';
Y = [ones(size(T))  T  T.^2]*A;
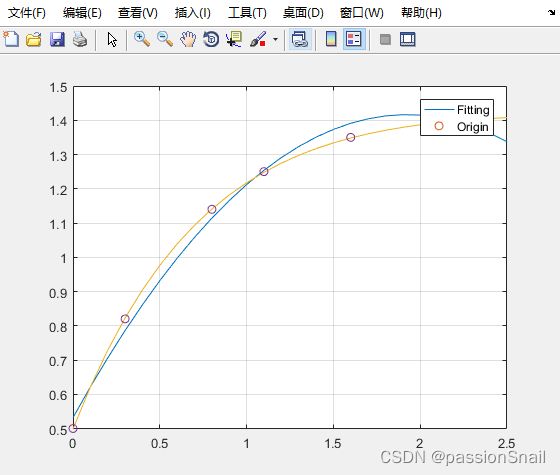
plot(T,Y,'-',t,y,'o')
grid on
legend('Fitting','Origin')
hold on;        % 保留之前绘制的曲线

%% 
X = [ones(size(t))  exp(-t)  t.*exp(-t)];
A = X\y;
T = (0:0.1:2.5)';
Y = [ones(size(T))  exp(-T)  T.*exp(-T)]*A;
plot(T,Y,'-',t,y,'o')
grid on
legend('Fitting', 'Origin')

做最小二乘拟合：polyfitpolyval

close all
clear
clc

%%
x = 0:.1:10;
y = sin(x)+cos(2*x);

%% 5次多项式拟合a
k5 = polyfit(x,y,5);    % 得到5次多项式系数
y5 = polyval(k5, x);    % 得到离散的数值

%% 11次多项式拟合
k11 = polyfit(x,y,11);
y11 = polyval(k11, x);

%% 绘制数据曲线
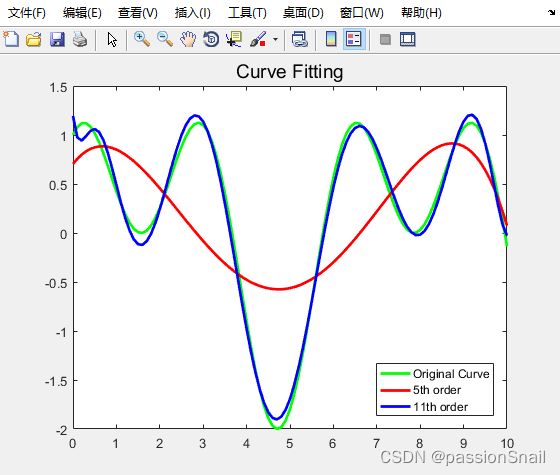
plot(x, y, 'g', x, y5, 'r', x, y11, 'b')

%% 标注
title('Curve Fitting', 'Fontsize',14)
legend('Original Curve', '5th order', '11th order','Location','southeast')
set(findobj('Type', 'line'), 'LineWidth', 2)

运用次方越多，和函数越接近，但是运算量也会变大。如果你的数据精度够高，可以尝试高次的拟合；反之，若你只需要获得数据的大趋势，低次的拟合可能效果更好。总而言之，Matlab 只是工具，关键看对知识的理解和如何运用公式。

3 图形界面曲线拟合

Matlab 提供了基本的曲线拟合图像工具，利用这个界面可以完成以下工作：

• 使用三次样条曲线(cubic spline)或最高10阶的多项式拟合数据

• 对一组给定的数据同时绘制多条拟合曲线

• 绘制拟合残差曲线

• 查看拟合的数值结果

• 对拟合曲线求值(内插或外推)

• 用拟合数值结果和残差的范数标注图形

• 把拟合的结果保存到 MATLAB工作区

使用基本的曲线拟合工具，以 Matlab 自带的 Demo 为例 help census :

3.1 加载数据

  clear
  clc
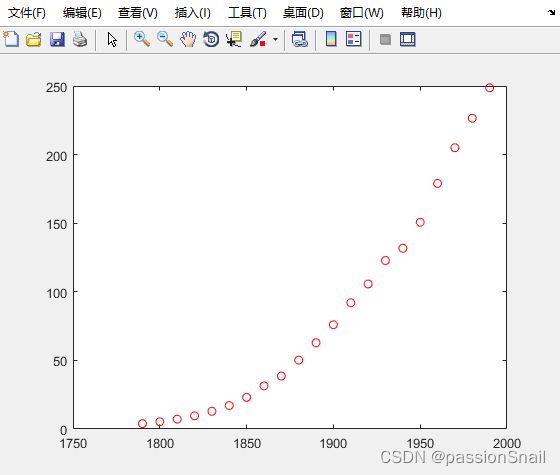
  load census         % 美国每十年的人口数据
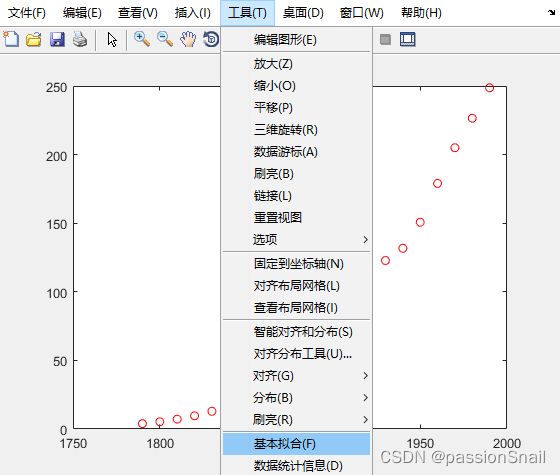
  plot(cdate,pop,'ro');

3.2 图形化拟合

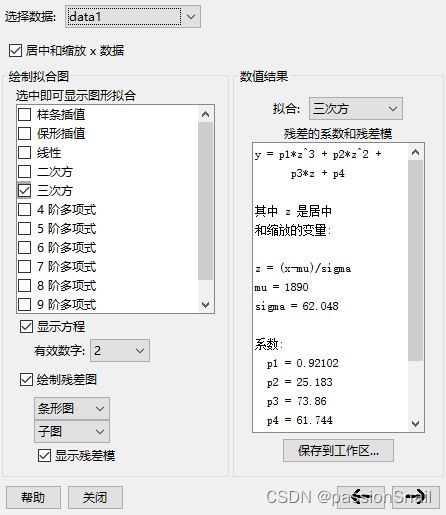
在 figure 窗口点击 工具 → 基本拟合 ，后续可以选择中心化并缩放 X 数据、拟合方式、绘制残差图、显示残差模等，之后 保存到工作区

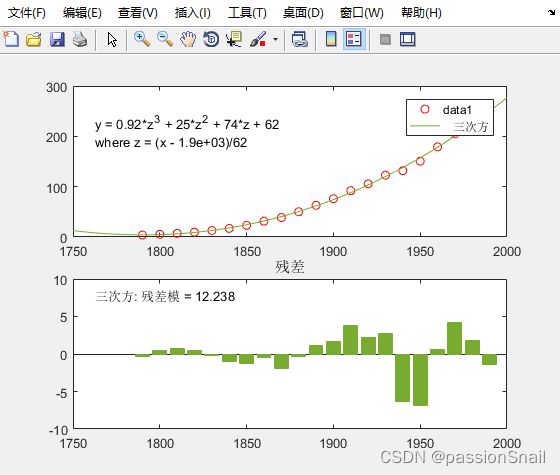
3.3 拟合结果

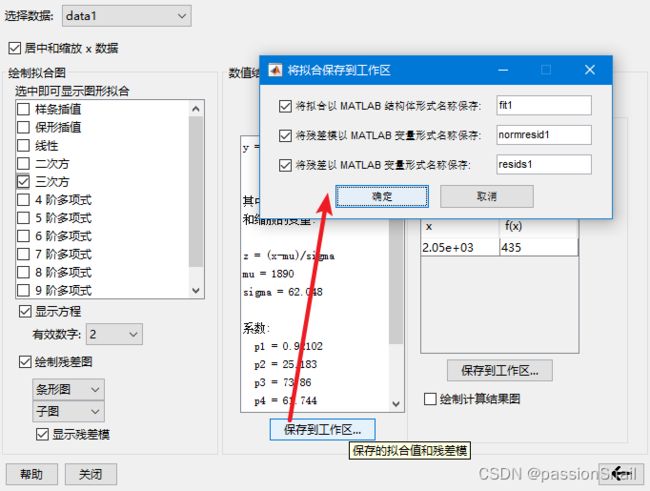
3.4 保存数据

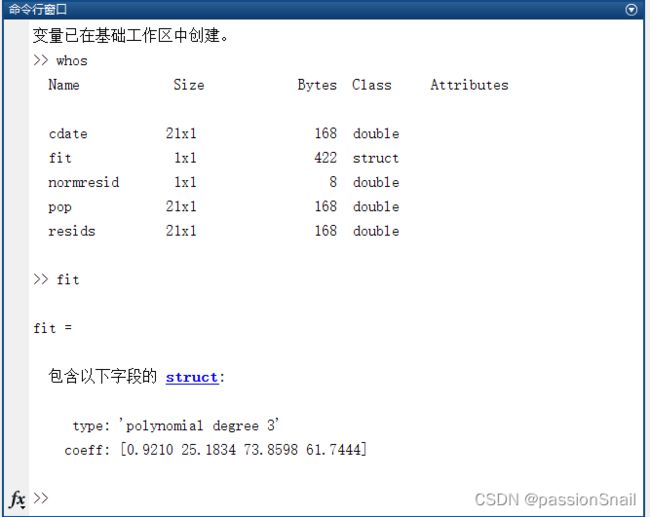
3.5 查看数据

  whos
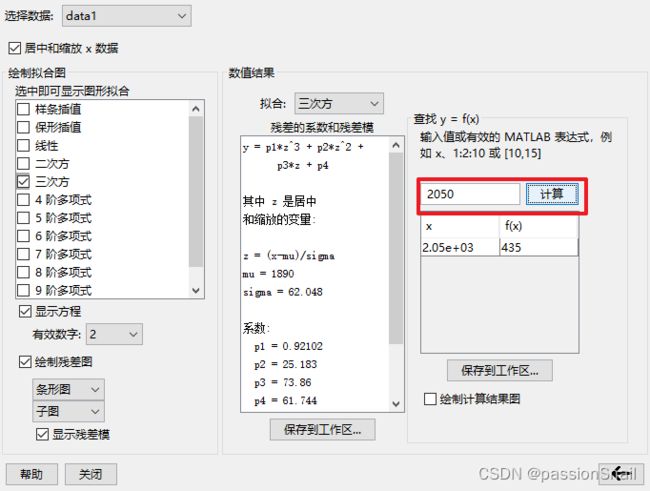
  fit

3.6 拟合预测

之后可以继续扩展使用工具箱，计算到 2050 年的计算结果