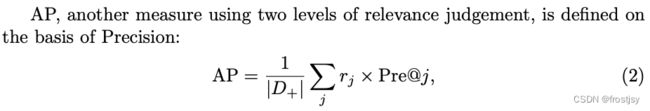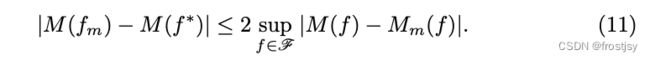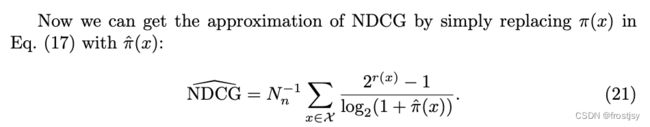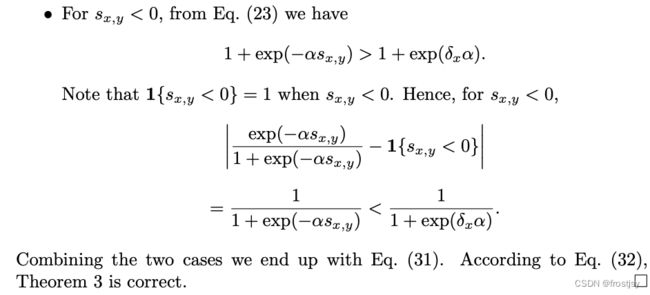信息检索指标直接优化的通用近似框架
1、直接优化信息检索指标的背景
1.1、存在问题
直接优化信息检索的指标是信息检索的一大方向。主要包含两类方法，一类是将IR指标作为上界进行优化；另一类是使用平滑函数近似表示IR指标进行优化。
- 直接优化IR指标方式很自然，但没有提供理论支持。
- 代理函数与IR指标之间的关系未充分得到论证，代理函数是否能够表述IR指标的度量在优化过程中很有必要。
- 现有代理函数不容易优化，很难扩展到其他的指标。例如
、
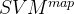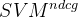采用结构化的SVM来优化ap和ndcg指标。
1.2、提出优化框架解决问题
提出了一个优化框架来直接优化IR指标，可以有效避免下列3个问题
- 基于统计学的一致性理论，在大量数据情况下，IR指标有界代理函数不是很复杂时，直接优化IR指标有较好的表现。基于泛化理论，进一步论证了直接优化IR指标的效果。
- 提出的框架可以准确近似地表示任何基于位置的IR指标，并将IR的优化转换为代理函数的优化。直接优化IR 度量指标的难点在于，度量是基于位置的，基于位置的指标不连续也不可微。如果可以连续可微地表示基于位置的度量，则可以优化任何基于位置的度量指标。实验表明，高精度近似表示，高效率。
- 很容易导出学习算法来优化框架中的代理函数
1.3、主要贡献
- 为直接优化IR 指标提供了理论依据
- 提供了一个基于位置的IR指标度量框架
- 给出了ap和ndcg两个指标优化的示例
2、相关工作
2.1、常见IR 指标
2.1.1、p@k
top k个doc中相关doc的比例
2.1.2、ap
两级相关性判断的标准,位置平均的p@k
2.1.3、map
所有query的ap均值
2.1.4、NDCG@k
NDCG@k是多级相关性评估标准的IR评估指标
2.2、直接优化IR指标的常见方法
直接优化1-ap的上界
直接优化1-ndcg的上界
AdaRank设定为指数函数，该函数可以设定为1-ap、1-ndcg的上界
SoftRank将随机性引入相关性分数来平滑ndcg指标
3、理论论证
3.1、效果度量
为针对指标M的预期度量(测试度量)，
为针对指标M的经验度量(训练度量)，具体公式表示如下：
3.2、两个理论
3.2.1、理论1：一致性理论
如果排序函数空间F不复杂，并且IR度量M(q, f) 在函数空间 F 上一致有界，则训练
学习排序算法的效率M(f)一致收敛于测试效率M(f)。
对ndcg、map、p@k其范围为[0,1]之间，IR度量M(q, f)在函数空间上是一致有界的
3.2.2、理论2:泛化性理论
测试效率和最佳测试效率有上界，表述如下：
当query量足够大时，直接优化排序指标是最佳的优化方式
3.3、remarks
像DCG无界的指标，不满足理论1的一致有界条件，代理函数不能保证取得较好的效果。
两个理论只在大样本条件下成立
代理函数和IR指标的关系没有论证，无法保证直接优化的方式优于其他方式
4、IR指标代理框架
4.1、重要4步
- 1、重新定义IR指标，将IR指标按照依据位置索引的变更为依据doc索引。新定义的公式中包含位置函数和可选的截断函数，其中位置函数和截断函数不可导。
- 2、用rank score的平滑函数来近似位置函数
- 3、用位置平滑函数近似截断函数
- 4、应用优化技术来优化近似指标(代理函数)
4.2、IR指标定义
X为q的一系列doc，x为X中的一个，f为x的排序打分函数，x的分数记为
,其表述如下：
根据可以得到一个排序
,根据label会有一个原始的相关度排序r(x),和r(x)之间可以通过IR指标进行度量，公式化表示如下：
4.3、IR指标重新定义
4.3.1、ap指标重定义
4.3.2、ndcg指标重定义
重定义中的位置函数和截断函数均不可导
4.4、位置近似函数
4.4.1、排序分位置表示
位置可视为排序分的产出，位置和截断函数均不连续可导
4.4.2、平滑函数替代位置表示
用逻辑回归函数表示指示函数
sigmiod函数预测为0的部分
逻辑函数是sigmoid函数的特例，其他的sigmiod函数也满足要求
4.4.3、替换后的位置表示
用平滑函数替代后的位置表示
4.4.4、位置表示与近似位置表示对比
位置近似表示和真实表示几乎接近
4.5、截断函数近似
截断函数为两个分数的差值，可以将位置的差值直接进行sigmiod，引入截断函数表示后的ap指标表示如下所示：
4.6、代理函数优化
指标函数使其变得连续可微，简单的优化方法就能直接进行优化，使其最大。
5、理论分析
5.1、位置近似理论分析
正值最小差距表示
理论3：给定一个包含n个doc集的X，当
时，近似位置表示可以以如下精度接近真实位置表示
当
很大时，位置表示和近似位置表示接近
理论3证明
理论4:给定一个包含n个doc集的X,当
时，近似位置表示接近真实位置表示的精度在如下区间中
5.2、度量近似理论分析
理论5：误差
时，近似ap度量和真实ap度量精度上界如下：
理论6:ndcg度量的精度上界如下所示：
5.3、精度近似的理由
直接指标优化表现良好，近似指标精度高，能达到同等的效果。
理论7:近似度量在测试集上的表现和最优表现有上界
6、实验结论
6.1、数据集
采用LETOR5数据集来进行实验结果验证，LETOR上的TD2003 （50个query，每个对应1000个doc）和 TD2004（75个query，每个对应1000个doc，2个相关性等级（相关/不相关），44维query-doc对特征表示）去测试ApproxAP算法。LETOR上的OHSUMED（106个query，16,140个query-doc pair样本，3个相关性档位(完全相关、部分相关、不相关)，25维特征表示）被用来去测试ApproxNDCG算法。
6.2、IR指标近似度量
IR指标近似和真实IR指标之间的差距，AP、NDCG指标之间差距公式表示
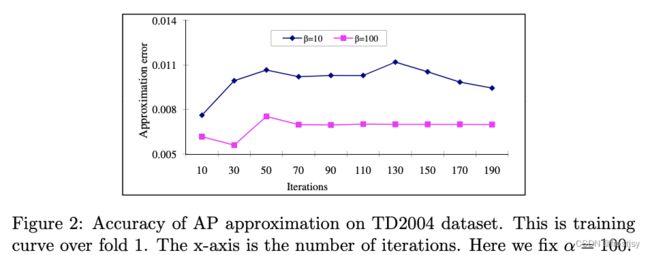
固定超参
=10，ap error随
超参变化的曲线图
=100时，近似IR指标估计和真实指标估计准确率高达98%
固定超参=100，ap error随超参变化的曲线图
ndcg度量精度和精度随超参变化的曲线
ndcg和ap能得出一样的结论
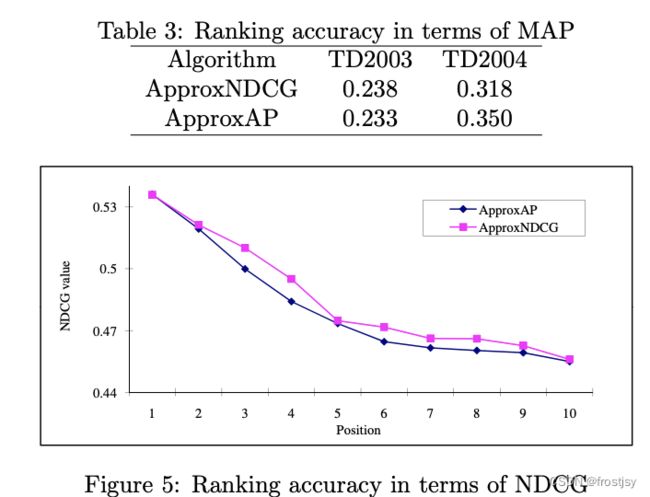
6.3、approxNDCG和approxAP的实验对比
6.3.1、approxAP指标
approxAP和AdaRank.MAP、SVMmap结果对比，AdaRank.MAP从论文中引用，SVMmap结果为论文作者提供参数跑出
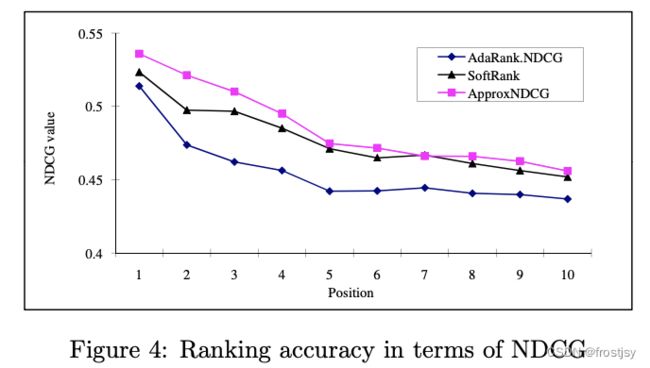
6.3.2、approxNDCG指标
NDCG@n指标在SoftRank、 AdaRank.NDCG 、 ApproxNDCG中的表现分别为0.6680, 0.6589 、 0.6698。
不同位置的表现，3种算法随位置的变化曲线如下：
6.4、讨论
选择哪个指标更加合适？
论文中给出，只有两个相关性等级时，使用MAP指标比较合适；当有多个相关性档位时，选择NDCG指标比较合适。
在训练时，就M指标，直接优化M指标是否比直接优化M'指标更好？
如果指标M'包含了M,优化M'可能比优化M更好
在TD2003数据集上approxAP和approxNDCG表现相当，在TD2004数据集上approxAP较approxNDCG表现好。直接优化M指标是否比直接优化M'指标无法定论，还有待调研论证。
7、总结
此paper为直接优化IR指标提供了理论依据；在一定条件下，直接优化IR指标是合理的；直接优化指标可能是排序学习最优的方法之一。
提出了基于位置IR指标直接优化的整体框架，核心思想在于使用排序分近似表述IR指标。主要有3个优点，1）近似估计法简单通用；2) 许多现有技术可以直接用于优化，且优化本身是与测量无关的；3）设置合理的参数可以获得较高的近似逼近。以ap和ndcg为例，展示了如何优化框架，在公开数据集上验证了理论分析的正确性和有效性。
8、参考文献
https://arxiv.org/pdf/2102.07831.pdf NeuralNDCG
排序学习-4.ApproxNDCG与NeuralNDCG - 知乎
https://www.microsoft.com/en-us/research/wp-content/uploads/2016/02/tr-2008-164.pdf ApproxNDCG