数据结构分析:红黑树、B+树
数据结构分析:红黑树、B+树
前言
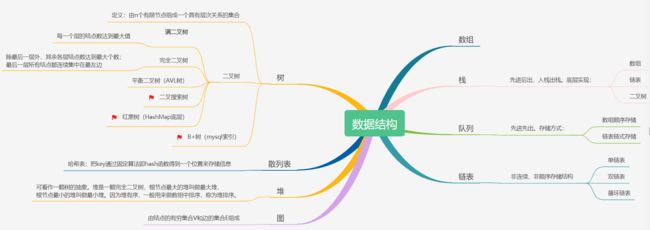
常见的数据结构大概分为以下8种,作为一个开发人员,数据结构是内功之一。 本文参考了网络上相关知识,加之自己的理解。简单说明红黑树、B+树的特性。
1. 二叉搜索树(Binary Search Tree,简称BST)
介绍红黑树之前先介绍下二叉搜索树的特点:
-
左子树不为空,则左子树上结点值小于根结点
-
右子树不为空,则右子树上结点值大于根结点
-
子树同样也要遵循以上两点
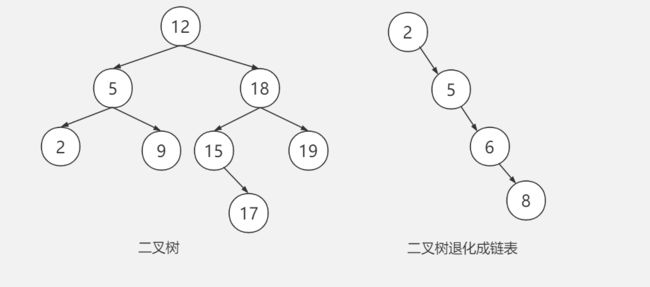
极端情况会退化成链表;时间复杂度就是树的深度O(n)。
所有就有了平衡的二叉查找树。
AVL树:平衡二叉树,它的左右子树高度之差不超过1,并且左右两个子树都是一棵平衡二叉树。时间复杂度O(logn)。
2. 红黑树(Red-Black Tree,以下简称RBTree)
红黑树是一种自平衡的二叉查找树(二叉搜索树、二叉排序树),高效的查找算法数据结构,特殊的二叉树。
性质:
-
每个结点不是红色就是黑色,
-
根结点是黑色,
-
每个叶子结点(NIL)都是黑色的空结点,
-
从根结点到叶子结点,不会出现两个连续的红色结点,
-
从任何一个结点出发到叶子结点,这条路径上都有相同数目的黑色结点。
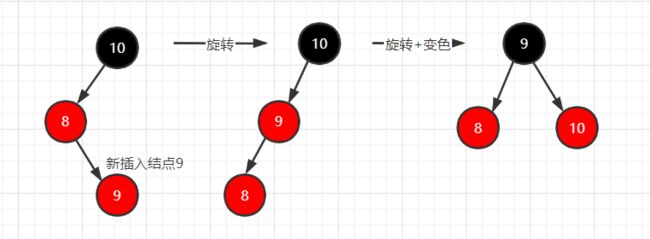
为了满足这些性质,因此需要变颜色,旋转。 旋转和颜色变换规则:所有插入的点默认为红色,只有这样数据结构才会变化。
变颜色情况:
如果当前结点的父亲是红色,且它的祖父结点的另一个子结点(叔叔结点)也是红色,则:
-
把父结点设为黑色,
-
叔叔结点设为黑色,
-
把祖父结点设为红色,
-
指针指向祖父结点。
下面左旋、右旋规则前提:
新结点(当前插入结点)、父结点、祖父结点在同一条斜线上 适用下面规则。如不在一条斜线,hashmap红黑树源码是先做一次旋转,达到一条斜线,再左旋或右旋。
举例说明
左旋:
当前父结点是红色,叔叔是黑结点或空结点的时候,且当前的结点是右子树。左旋,则:
-
父结点变黑色;
-
祖父结点变红色;
-
以祖父结点旋转。
网图:左旋
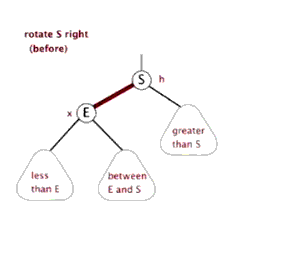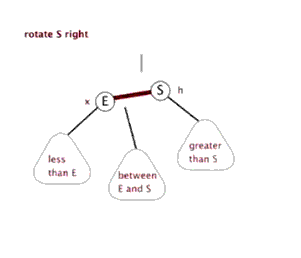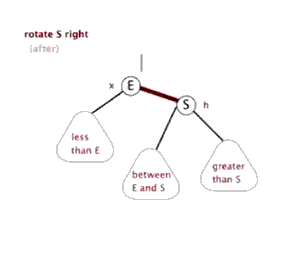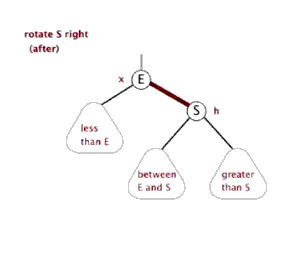
右旋:
当前父结点是红色,叔叔是结点或空结点的时候,且当前的结点是左子树。右旋,则:
-
把父结点变为黑色,
-
把祖父结点变为红色,
-
以祖父结点旋转。
网图:右旋
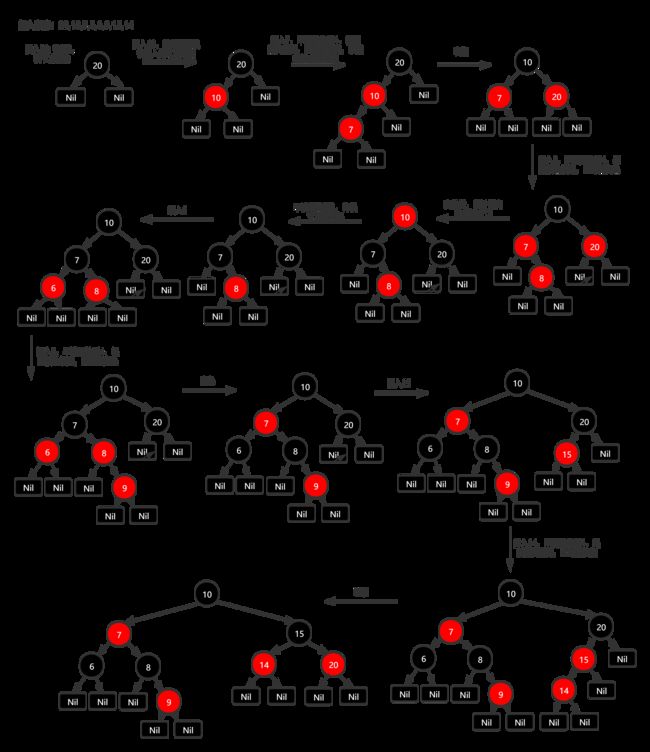
下图是我用processon画的插入过程,需要原图的可私我拿走。
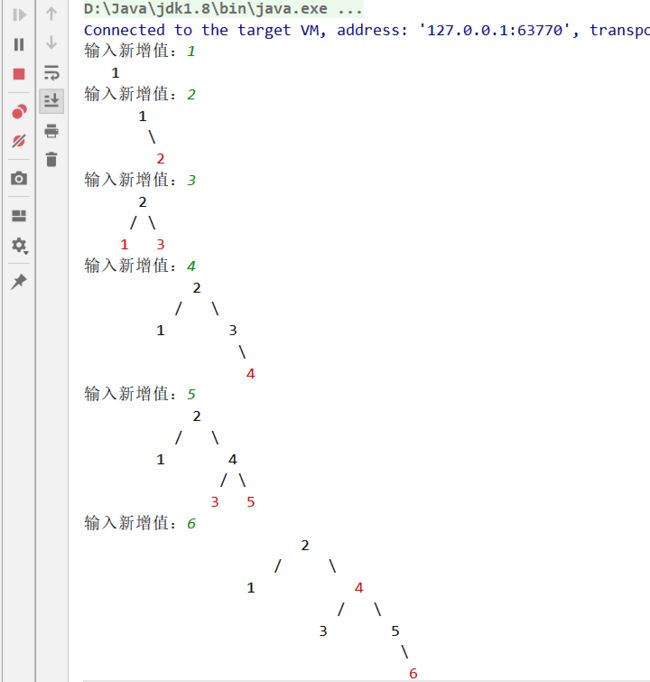
随机选了几个数字模拟插入过程;根结点是没有父结点的,入度为0。先插入20,若根结点为空,那么插入结点20作为根结点;再插入10,从根结点找,比20小,查找20的左子树,为空,则插入。查找插入位置同二叉搜索树一样,找到后插入,再看是否需要变颜色或者旋转,防止退化成链表。
原创:可点击放大
红黑树删除操作
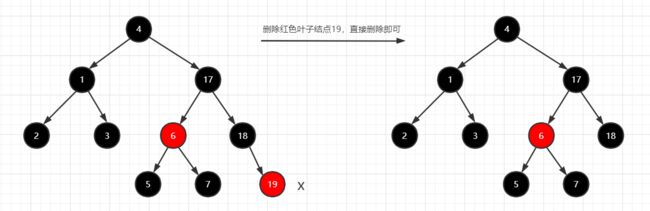
- 删除叶子结点:
-
红色结点直接删除 ①
- 黑色叶子结点,做删除平衡操作:
-
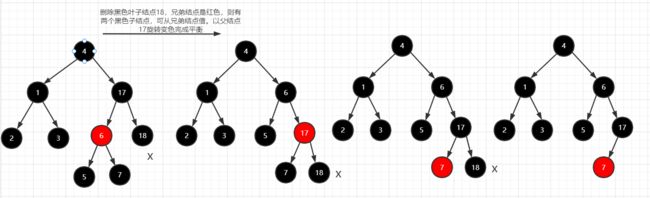
兄弟结点是红色,则兄弟结点必有两个黑色子结点。② [以兄弟结点这条线旋转,变色,替补删除的结点]
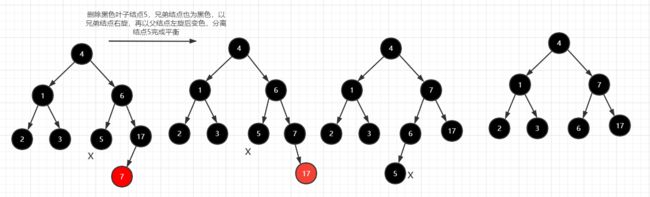
- 兄弟结点是黑色:
-
有子结点,子结点必为红色。③ [以兄弟结点这条线旋转,变色,完成平衡操作]
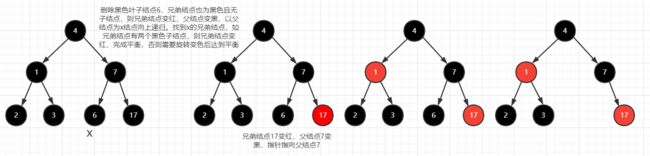
-
没子结点。④ [兄弟结点变红,父结点变黑,指针指向父结点递归完成平衡]
-
-
-
- 删除非叶子结点:
-
有一个子结点,子结点必为红色。⑤ [用子结点替换后做平衡操作]
-
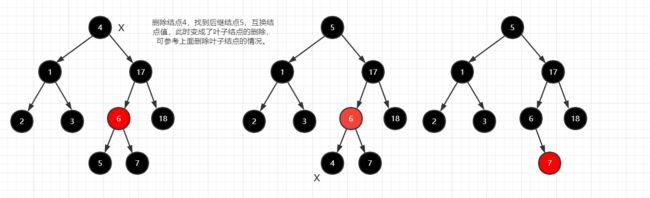
有两个子结点则找后继结点(大于当前结点的最小结点)。⑥ [找到后继结点,作为替换结点,此时就变成了删除叶子结点的情况]
-
图①
图②
图③
图④
图⑤
图⑥
JDK HashMap红黑树源码
为了简单分析,微调了部分代码,删除了部分代码:
static final class TreeNode> {
K key;
TreeNode parent; // red-black tree links
TreeNode left;
TreeNode right;
boolean red;
TreeNode(K key) {
this.key = key;
}
TreeNode getLeft() {
return this.left;
}
TreeNode getRight() {
return this.right;
}
boolean isColor() {
return !this.red;
}
K getValue(){
return key;
}
/**
* Returns root of tree containing this node.
*/
final TreeNode root() {
for (TreeNode r = this, p;;) {
if ((p = r.parent) == null)
return r;
r = p;
}
}
/**
* 查找结点是否存在
* @param key
* @param p 初始传入root结点查询
* @return
*/
final TreeNode find(TreeNode p, Object key) {
if (p == null) {
return null;
}
int k = p.key.compareTo(key);
if (k > 0) {
p = find(p.left, key);
}
else if (k < 0) {
p = find(p.right, key);
}
return p;
}
/**
* 插入结点
* @param key
* @return
*/
final TreeNode insert(TreeNode root, int key) {
if (root == null) {
return null;
}
TreeNode p = new TreeNode(key);
while (true) {
int k = root.key.compareTo(key);
if (k > 0) {
if (root.left == null) {
p.parent = root;
root = root.left = p;
break;
}
root = root.left;
}
else if (k < 0) {
if (root.right == null) {
p.parent = root;
root = root.right = p;
break;
}
root = root.right;
}
else {
break;
}
}
return root;
}
/**
* 红黑树插入平衡
* @param root
* @param x
* @return
*/
static TreeNode balanceInsertion(TreeNode root, TreeNode x) {
//默认插入为红色
x.red = true;
//xp: 当前结点父节点 xpp:当前结点爷爷结点 xppl: 当前结点左叔叔节点 xppr: 当前结点右叔叔节点
for (TreeNode xp, xpp, xppl, xppr;;) {
//x结点父结点为空,说明当前x结点是根结点,根节点是黑色。
if ((xp = x.parent) == null) {
x.red = false;
return x;
}
//xp结点为黑色,说明插入当前结点不会破坏红黑树性质,直接返回根节点
//xp结点为红色的情况,则xp的父结点xpp不可能为空,假如为空,说明xp为红色的根结点,这样不符合红黑树性质。 这里如果说的不对请指出
else if (!xp.red || (xpp = xp.parent) == null) {
return root;
}
//判断条件:当前父结点为爷爷结点的左子树,大家可以画个图,贼清晰
if (xp == (xppl = xpp.left)) {
//当前结点x的爷爷结点xpp 的右子树xppr不为空,并且为红色结点,则变颜色。根据我上面写的变色规则,如果当前结点父亲和叔叔结点
//都是红色,则变色。父亲和叔叔结点变黑,爷爷结点变红,指针指向爷爷结点
if ((xppr = xpp.right) != null && xppr.red) {
xppr.red = false;
xp.red = false;
xpp.red = true;
x = xpp;
}
//这里有两种情况
//1.xppr结点为空,为空则xp结点两个子结点一个为空,一个为当前结点x, x可能在左子树或右子树
//2.如果xppr为黑色结点,则xp结点两个子结点一个为黑色结点,一个为当前结点x, x可能在左子树或右子树
else {
//如果当前结点为xp父结点的右节点,则左旋 (先左旋,再右旋)
//如果当前结点为xp父结点的左结点 (少一步左旋操作,直接右旋)
if (x == xp.right) {
//左旋
root = rotateLeft(root, x = xp);
//
xpp = (xp = x.parent) == null ? null : xp.parent;
}
//两个红节点,右旋
if (xp != null) {
//将父结点变黑
xp.red = false;
if (xpp != null) {
//爷爷结点变红
xpp.red = true;
//右旋
root = rotateRight(root, xpp);
}
}
}
}
else {
if (xppl != null && xppl.red) {
xppl.red = false;
xp.red = false;
xpp.red = true;
x = xpp;
}
else {
//先右旋,再左旋
if (x == xp.left) {
root = rotateRight(root, x = xp);
xpp = (xp = x.parent) == null ? null : xp.parent;
}
if (xp != null) {
xp.red = false;
if (xpp != null) {
xpp.red = true;
root = rotateLeft(root, xpp);
}
}
}
}
}
}
/**
* 左旋
* @param root
* @param p
* @return
*/
static TreeNode rotateLeft(TreeNode root, TreeNode p) {
//当前旋转的结点为p, 定义r为当前结点的右子结点,pp为当前p结点的父结点,rl为r结点的左结点
TreeNode r, pp, rl;
//左旋提前是当前结点不为空,且当前结点的右子节点不为空
if (p != null && (r = p.right) != null) {
//r结点左子结点rl不为空,则rl的父结点指向p
if ((rl = p.right = r.left) != null) {
rl.parent = p;
}
//如果p的父结点为空,说明p是根节点,左旋后,r为根结点,则r的颜色涂黑
if ((pp = r.parent = p.parent) == null) {
(root = r).red = false;
}
//如果p的父结点不为空,且p结点为pp的左子结点,则pp的左子树指向r
else if (pp.left == p) {
pp.left = r;
}
//p结点为pp的右子结点,pp的右子树指向r
else {
pp.right = r;
}
//r的左子树指向p
r.left = p;
//p的父结点指向r
p.parent = r;
}
return root;
}
/**
* 右旋
* @param root
* @param p
* @return
*/
static TreeNode rotateRight(TreeNode root, TreeNode p) {
//当前旋转的结点为p, 定义l为当前结点的左子结点,pp为当前p结点的父结点,lr为l结点的右结点
TreeNode l, pp, lr;
//右旋提前是当前结点不为空,且当前结点的左子节点不为空
if (p != null && (l = p.left) != null) {
//l结点右子结点lr不为空,则lr的父结点指向p
if ((lr = p.left = l.right) != null) {
lr.parent = p;
}
//如果p的父结点为空,说明p是根节点,右旋后,l为根结点,则l的颜色涂黑
if ((pp = l.parent = p.parent) == null) {
(root = l).red = false;
}
//如果p的父结点不为空,且p结点为pp的右子结点,则pp的右子数指向l
else if (pp.right == p) {
pp.right = l;
}
//p结点为pp的左子结点,pp的左子树指向r
else {
pp.left = l;
}
//l的右子树指向p
l.right = p;
//p的父结点指向l
p.parent = l;
}
return root;
}
/**
* 删除节点p
* @param root
* @param p
*/
final TreeNode removeTreeNode(TreeNode root, TreeNode p) {
//定义当前删除结点为p, pl为p的左结点,pr为p的右结点, replacement为替代结点
TreeNode pl = p.left, pr = p.right, replacement;
//左结点和右结点都不为空
if (pl != null && pr != null) {
TreeNode s = pr, sl;
while ((sl = s.left) != null){
// find successor 找后继结点
s = sl;
}
// swap colors 交换后继结点和p结点颜色
boolean c = s.red; s.red = p.red; p.red = c;
TreeNode sr = s.right;
TreeNode pp = p.parent;
if (s == pr) {
//p是后继结点s的父结点,则p的父结点指向s, s右节点指向p
p.parent = s;
s.right = p;
}
else {
//此时sp == pr, 改变s和p的指针
TreeNode sp = s.parent;
if ((p.parent = sp) != null) {
if (s == sp.left) {
sp.left = p;
} else {
sp.right = p;
}
}
if ((s.right = pr) != null) {
pr.parent = s;
}
}
//p之前关联的左结点指向空
p.left = null;
if ((p.right = sr) != null) {
sr.parent = p;
}
//改变pl的父结点,从p变为s
if ((s.left = pl) != null) {
pl.parent = s;
}
//s父结点不为空,则看p是在左结点还是右节点,替换成s
if ((s.parent = pp) == null) {
root = s;
}
else if (p == pp.left) {
pp.left = s;
}
else {
pp.right = s;
}
//后继结点的右结点sr不为空,则sr为替代结点,否则后继结点为替代结点
if (sr != null) {
replacement = sr;
}
else {
replacement = p;
}
}
//如果左结点pl或pr不为空,则pl或pr为红色结点
else if (pl != null) {
replacement = pl;
}
else if (pr != null) {
replacement = pr;
}
//替代结点为待删除结点p, 也就是叶子结点
//叶子结点分两种情况:红色,黑色
else {
replacement = p;
}
//替代结点不等于当前结点,则分离当前结点,当前结点父结点指向替代结点
if (replacement != p) {
TreeNode pp = replacement.parent = p.parent;
if (pp == null) {
root = replacement;
}
else if (p == pp.left) {
pp.left = replacement;
}
else {
pp.right = replacement;
}
p.left = p.right = p.parent = null;
}
//如果待删除结点为黑色结点,则进行删除平衡操作
TreeNode r = p.red ? root : balanceDeletion(root, replacement);
// detach
if (replacement == p) {
//删除结点为替换结点,则分离
TreeNode pp = p.parent;
p.parent = null;
if (pp != null) {
if (p == pp.left) {
pp.left = null;
}
else if (p == pp.right) {
pp.right = null;
}
}
}
return r;
}
/**
* 红黑树删除平衡
* @param root
* @param x 替代结点
* @return
*/
static TreeNode balanceDeletion(TreeNode root, TreeNode x) {
//定义x为当前结点,xp为x的父结点,xpl为父结点的左子结点,xpr为父结点的右子结点
for (TreeNode xp, xpl, xpr;;) {
if (x == null || x == root) {
return root;
}
else if ((xp = x.parent) == null) {
x.red = false;
return x;
}
//如果x为红色结点,涂黑
else if (x.red) {
x.red = false;
return root;
}
//x为父结点的左子结点
else if ((xpl = xp.left) == x) {
//父结点的右结点不为空且为红色结点
if ((xpr = xp.right) != null && xpr.red) {
//父结点变红,父结点的右结点变黑,以父结点左旋
xpr.red = false;
xp.red = true;
root = rotateLeft(root, xp);
TreeOperation.show(root);
//改变指针,上面旋转后xpr变成了xp的父结点,所以xpr的结点重新指向
xpr = (xp = x.parent) == null ? null : xp.right;
}
if (xpr == null) {
x = xp;
}
else {
//此时xpr为x的兄弟结点,判断兄弟结点的左右子结点是否为空或为黑色结点,
//如满足,则兄弟结点变红,指针指向父结点,以父结点为x结点继续做删除平衡操作
TreeNode sl = xpr.left, sr = xpr.right;
if ((sr == null || !sr.red) && (sl == null || !sl.red)) {
xpr.red = true;
x = xp;
}
else {
if (sr == null || !sr.red) {
if (sl != null) {
//x兄弟结点右孩子为空或为黑色结点,且左孩子不为空,则涂黑
sl.red = false;
}
//x兄弟结点变红,以兄弟结点右旋
xpr.red = true;
root = rotateRight(root, xpr);
TreeOperation.show(root);
//改变xp的右指针,xpr指向sl结点
xpr = (xp = x.parent) == null ? null : xp.right;
}
//x的兄弟结点xpr修改成父结点的颜色,右子结点不为空变黑,父结点变黑,以父结点左旋
if (xpr != null) {
xpr.red = (xp == null) ? false : xp.red;
if ((sr = xpr.right) != null) {
sr.red = false;
}
}
if (xp != null) {
xp.red = false;
root = rotateLeft(root, xp);
TreeOperation.show(root);
}
x = root;
}
}
}
else {
if (xpl != null && xpl.red) {
xpl.red = false;
xp.red = true;
root = rotateRight(root, xp);
TreeOperation.show(root);
xpl = (xp = x.parent) == null ? null : xp.left;
}
if (xpl == null) {
x = xp;
}
else {
TreeNode sl = xpl.left, sr = xpl.right;
if ((sl == null || !sl.red) && (sr == null || !sr.red)) {
xpl.red = true;
x = xp;
}
else {
if (sl == null || !sl.red) {
if (sr != null) {
sr.red = false;
}
xpl.red = true;
root = rotateLeft(root, xpl);
TreeOperation.show(root);
xpl = (xp = x.parent) == null ? null : xp.left;
}
if (xpl != null) {
xpl.red = (xp == null) ? false : xp.red;
if ((sl = xpl.left) != null) {
sl.red = false;
}
}
if (xp != null) {
xp.red = false;
root = rotateRight(root, xp);
}
x = root;
}
}
}
}
}
}
本地打印红黑树插入:
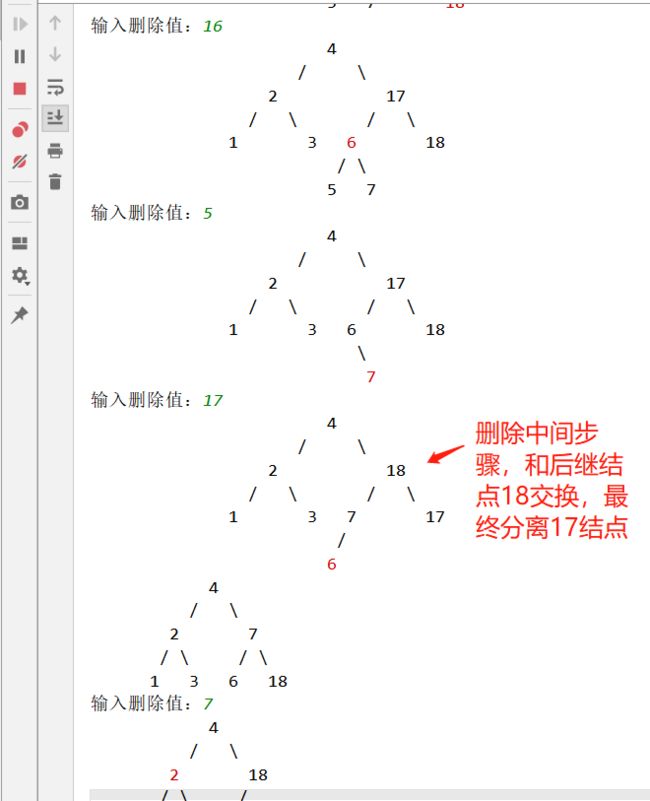
本地打印红黑树删除:
总结:
红黑树的复杂之处在于删除,删除需要变色,旋转来保持树的平衡。所以删除大概理解为:
-
红色叶子结点直接删除
-
黑色叶子结点则从兄弟结点借,兄弟结点有子结点,可借,通过旋转变色完成;兄弟结点没子结点,则递归父类做平衡
-
非叶子结点则找后继结点作为替换结点,就变成了叶子结点的删除。
B+树放在下一篇分析。(文中不对之处请指出,谢谢)