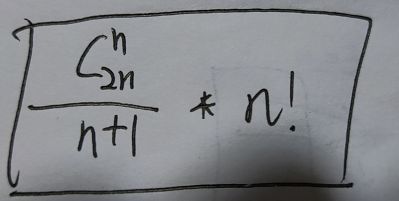根据前序遍历和中序遍历创建二叉树

欢迎关注我的微信公众号：MatlabGUI QtCPP等学习记录

Contents

前言四种遍历树的方法简介简介两种快速获得遍历结果的方法根据前序遍历和后续遍历创建树代码实现四种遍历树的方法的代码

前言

昨天参加了两场笔试，都考了这个题。第一场是根据pre_order和in_order把创建二叉树的代码写出来，第二场是根据pre_order和in_order把这个二叉树画出来！

当时第一场是C++开发的岗位的笔试，我没做出来，虽然代码写了，但是有Bug一直没改出来（主要还是不熟），他们不让在本地IDE中写，所以没法调试。。。所以第一场笔试我凉了。

第二场是和传感器有关的岗位，虽然这个画出来了，但是其他笔试题有的没学过（没学过那个专业课），有的忘了(比如概率统计)。考的太杂了，感觉也不行。。。

不说废话了，下面讲讲如何根据pre_order和in_order创建二叉树。

四种遍历树的方法简介

简介

首先这里简单介绍一下二叉树的4种遍历方式：

• 前序遍历（pre_order）

• 中序遍历（in_order）

• 后序遍历（post_order）

• 层序遍历（level_order）

至于这些遍历的代码放在文章的最后。

前序遍历就是先对当前的根节点进行操作，然后到左子节点，再到右子节点！

中序遍历就是先对当前左子节点进行操作，然后到当前根节点，再到右子节点！

后序遍历就是先对当前左子节点进行操作，然后到右子节点，再到当前根节点！

层序遍历就是按照从上到下从左到右的顺序对每个节点进行操作！代码写起来比前三个复杂点，得借助队列，并用迭代的方式来做。

如下图(之前上课做的笔记)：

两种快速获得遍历结果的方法

另外，介绍两个 可以快速地 根据树的形状 得出 前序、后序、中序 的遍历结果。

法一：

法二：

根据前序遍历和后续遍历创建树

给你一个数组，用这个数组的值来创建一个树，结果有多种可能：

其中n是数组中元素的个数！

但是，如果我们给了两个数组，分别是前序遍历和后续遍历的结果，那么我们就能创建唯一的一个树！

Note：要求数组中的元素不重复，是唯一的！

看过上面对树的那几种遍历方式后，可以发现：

Note：下面的这个过程有点枯燥，我表述地也不太好，可以看后面的图。

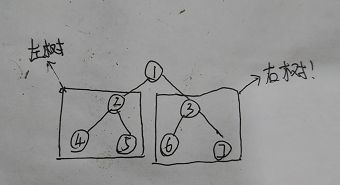
• 前序遍历的第一个元素就是树的根节点；第二个元素是根节点的左子节点，这个左子节点也是后面的根节点；

• 根节点把中序遍历的数组一分为二，中序遍历的数组中：根节点的左边是左树，根节点的右边是右树

• 

• 所以，我们就对前序遍历的数组进行遍历，当前索引记为pre_i，在每次遍历中，到中序遍历的数组中找这个pre_i对应的值，用这个pre_i把中序遍历的结果一分为二。这样往复下去就能还原树了。

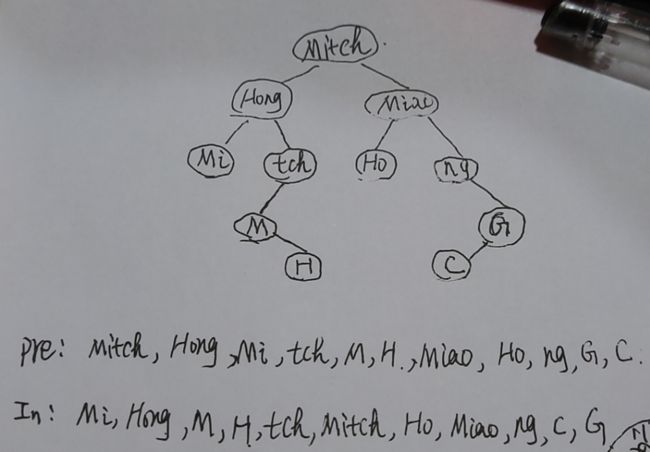
下面我画一下整个流程：

大概就是这样，不断地对中序遍历的数组一分为二（根据前序遍历的数组的当前元素进行分割）；中序遍历的数组的当前元素就是当前的根节点。

代码实现

先定义树的节点：

template 
struct Node{
    T val;
    Node* left;
    Node* right;

    explicit Node(T v) : val(v), left(nullptr), right(nullptr){}
};

根据前序遍历和中序遍历创建树：

/**
 * @brief 根据前序遍历和中序遍历创建树
 * @param[in] pre_vec   前序遍历的数组
 * @param[in] in_vec    中序遍历的数组
 * @param[in] left_in   中序遍历当前段的左边界
 * @param[in] right_in  中序遍历当前段的右边界（超尾）
 * @static pre_i        前序遍历的当前的索引
 *
 * @note 在每一层递归中，当前的 中序遍历 数组段 被分为：[left_in, pre_i), pre_i, [pre_i+1, right_in)
 * */
template 
Node* CreateTreeR(vector& pre_vec, vector& in_vec, int left_in, int right_in)
{
    static int pre_i = 0;

    if (left_in < right_in)
    {
        /// 从 前序遍历 的数组中 获取 当前 根节点！
        T cur_root_val = pre_vec.at(pre_i);
        auto* cur_root = new Node(cur_root_val);

        /// 遍历 中序遍历 的数组，找到当前根节点对应的索引
        int i = left_in;
        while (i < right_in && cur_root_val != in_vec.at(i)) ++i;

        /// 下次递归前 pre_i 是需要向后移动一位的
        ++pre_i;

        /// 一分为二！(注意，i是当前节点的索引哦！)
        cur_root->left  = CreateTreeR(pre_vec, in_vec, left_in, i);              /// 左树
        cur_root->right = CreateTreeR(pre_vec, in_vec, i+1, right_in);   /// 右树

        return cur_root;
    }

    /// 当分到只剩最后一个元素时就返回空了
    return nullptr;
}

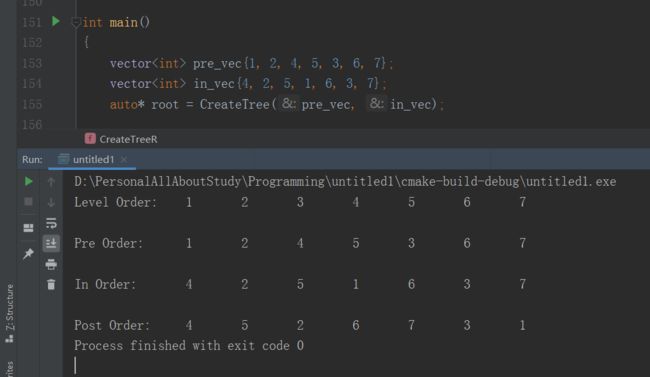
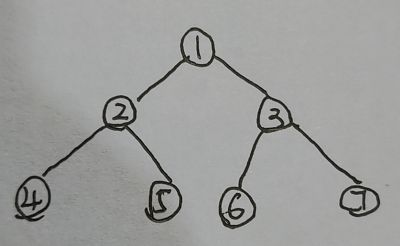
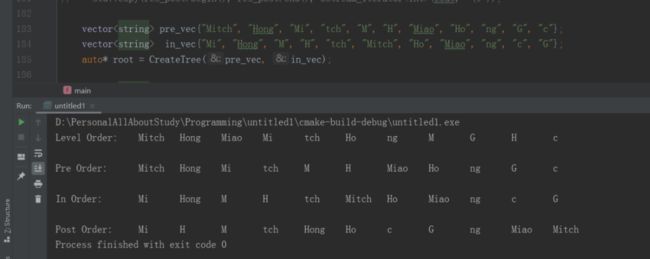
测试这段程序

对创建出来的这个树，用四种遍历方法分别遍历一下子，四种遍历的代码在文末。

 

---

上面这个是数字的，我现在拿字符串的试试：

 

---

四种遍历树的方法的代码

1.层序遍历：

/**
 * @brief 树的层序遍历
 * */
 template
 void LevelOrder(Node* root, vector& vec)
{
     /// 如果根节点为空就直接返回
     if (!root) return;

     /// 定义一个队列放所有可能会成为 "根节点" 的节点（每次循环中都会pop出一个 "根节点" ）
     queue< Node* > q;
     q.push(root);

     while (!q.empty())
     {
         /// 从队列中拿出最前面的根节点
         Node* cur_root = q.front();  /// 这个变量在while外面声明更好，不用每次都创建一个新变量。
         q.pop();
         /// 保存当前 "根节点" 的值
         vec.push_back(cur_root->val);

         /// 如果左子节点非空就把左子节点放入队列
         if (cur_root->left)
             q.push(cur_root->left);

         /// 如果右子节点非空就把右子节点放入队列
         if (cur_root->right)
             q.push(cur_root->right);
     }
}

2.前序遍历：

/**
 * @brief 树的前序遍历
 * */
template
void PreOrder(Node* root, vector& vec)
{
    if (root)
    {
        vec.push_back(root->val);
        PreOrder(root->left, vec);
        PreOrder(root->right, vec);
    }
}

3.中序遍历：

/**
 * @brief 树的中序遍历
 * */
template
void InOrder(Node* root, vector& vec)
{
    if (root)
    {
        InOrder(root->left, vec);
        vec.push_back(root->val);
        InOrder(root->right, vec);
    }
}

4.后序遍历：

/**
 * @brief 树的后序遍历
 * */
template
void PostOrder(Node* root, vector& vec)
{
    if (root)
    {
        PostOrder(root->left, vec);
        PostOrder(root->right, vec);
        vec.push_back(root->val);
    }
}

---