海明码（Hamming Code）：利用奇偶校验矩阵纠错

本文主要介绍如何利用奇偶校验矩阵（Parity Check Matrix）进行纠错。

 

关于如何产生奇偶校验矩阵的方法：https://blog.csdn.net/weixin_57915039/article/details/117523933?spm=1001.2014.3001.5501

 

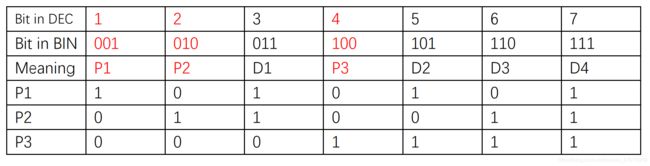
我们可以知道，奇偶校验矩阵H确定了每个奇偶校验位的 “管辖范围”。

如：

1=001

2=010

4=100

8=1000

16=10000

etc.

即：

P1对 xxxx1 的数进行奇偶校验。

P2对 xxx1x 的数进行奇偶校验。

P3对 xx1xx 的数进行奇偶校验。

.......

除此之外，H可以随着输入海明码的总长而进行改变，并且遵循H的每一列都是位置的二进制表示，即H=( 1, 2, 3, ....., 总长)。

 

利用奇偶校验矩阵纠错

 

既然奇偶校验矩阵H确定了每个奇偶校验位的 “管辖范围”，那么如果我们让奇偶校验矩阵H乘以编码过后的海明码 (没有错误的），每一行都能将奇偶校验位和它的 “管辖范围” 给提出来。

 

此时如果模二处理，那么结果将会是三个0。

原因是，正确的海明码都已经进行了偶校验，1的个数会是偶数，模二为0.

即：

 

此时，我们把编码后的海明码中的其中一位翻转（一位的原因是海明码无法处理多个错误）。

 

这个时候H和有错误的海明码相乘的结果将会变成错误位置的二进制表示！

我们接下来只需把错误位置翻转就能实现查错纠错功能。