【力扣——动态规划】整理题目1：基础题目：509、70、746、62、63、343、96（附链接、题目描述、解题方法及代码）

如果对你有帮助的话
为博主点个赞吧
点赞是对博主最大的鼓励
爱心发射~

【动态规划整理合集】
【力扣—动态规划】整理题目1：基础题目：509、70、746、62、63、343、96
【力扣—动态规划】整理题目2：背包问题：0-1背包、完全背包

代码随想录知识星球

动态规划总结

基础知识

• 动态规划是由前一个状态推导出来的
• 而贪心算法是局部直接选最优的

解题步骤

1. 确定dp数组（dp table）以及下标的含义
2. 确定递推公式
3. dp数组如何初始化
4. 确定遍历顺序
5. 举例推导dp数组

解题步骤-简洁

1. 确定dp数组下标含义
2. 递推公式
3. 初始化
4. 遍历顺序
5. 推导结果

509. 斐波那契数

力扣

动态规划

class Solution {
    public int fib(int n) {
        /*
            动态规划:
                1. 确定dp数组（dp table）以及下标的含义
                    - 第i个斐波那契数 的值
                2. 确定递推公式
                    - F(n) = F(n - 1) + F(n - 2)
                3. dp数组如何初始化
                    - F(0) = 0，F(1) = 1
                4. 确定遍历顺序
                    - 从前到后
                5. 举例推导dp数组
                    - 0 1 1 2 3 5 8 13 21 34 55
        */
        if(n < 2) return n;
        int a=0, b=1, c=0;
        for(int i=1; i<n; ++i){
            c = a + b;
            a = b;
            b = c;
        }
        return c;
    }
}

70. 爬楼梯

力扣

动态规划

class Solution {
    public int climbStairs(int n) {
        /*
            动态规划：
                1. 确定dp数组（dp table）以及下标的含义
                    - 爬第n个台阶，有dp[n]种方法
                2. 确定递推公式
                    - dp[n] = dp[n-1] + dp[n-2]
                3. dp数组如何初始化
                    - dp[1]=1  dp[2]=2
                4. 确定遍历顺序
                    - 从前向后
                5. 举例推导dp数组
                    - 1、2、3、5、8
        */
        if(n<=2) return n;
        int a=1, b=2,c=0;
        for(int i=2; i<n; ++i){
            c = a + b;
            a = b;
            b = c;
        }
        return c;
    }
}

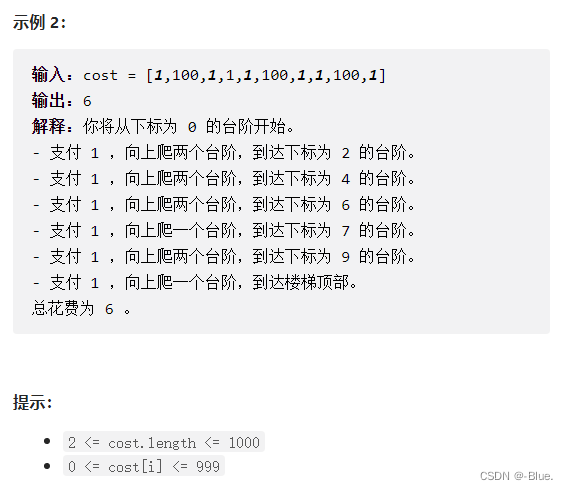
746. 使用最小花费爬楼梯

力扣

动态规划

class Solution {
    public int minCostClimbingStairs(int[] cost) {
        /*
            1. 确定dp数组（dp table）以及下标的含义
                - 到第i个台阶需要的最少体力
            2. 确定递推公式
                - dp[i] = min(dp[i - 1], dp[i - 2]) + cost[i];
            3. dp数组如何初始化
                - dp[0] = cost[0], dp[1] = cost[1]
            4. 确定遍历顺序
                - 从前向后
            5. 举例推导dp数组
        */
        if(cost == null || cost.length == 0) return 0;
        if(cost.length == 1) return cost[0];
        int[] dp = new int[cost.length];
        dp[0] = cost[0];
        dp[1] = cost[1];
        for(int i=2; i<cost.length; ++i){
            dp[i] = Math.min(dp[i-1], dp[i-2]) + cost[i];
        }
        return Math.min(dp[cost.length-1], dp[cost.length -2]);
    }
}

62. 不同路径

力扣

动态规划

class Solution {
    public int uniquePaths(int m, int n) {
        /*
            1. 确定dp数组下标含义—— dp[i][j] 到每一个坐标可能的路径种类
            2. 递推公式—— dp[i][j] = dp[i-1][j]+ dp[i][j-1]
            3. 初始化—— dp[i][0]=1 dp[0][i]=1 初始化横竖就可
            4. 遍历顺序—— 一行一行遍历
            5. 推导结果 
        */
        int[][] dp = new int[m][n];
        for(int i=0; i<m; ++i){
            dp[i][0] = 1;
        }
        for(int i=0; i<n; ++i){
            dp[0][i] = 1;
        }
        for(int i=1; i<m; ++i){
            for(int j=1; j<n; ++j){
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }
}

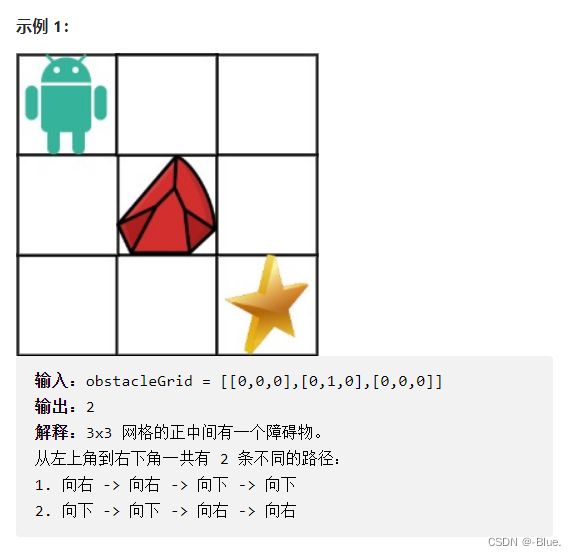
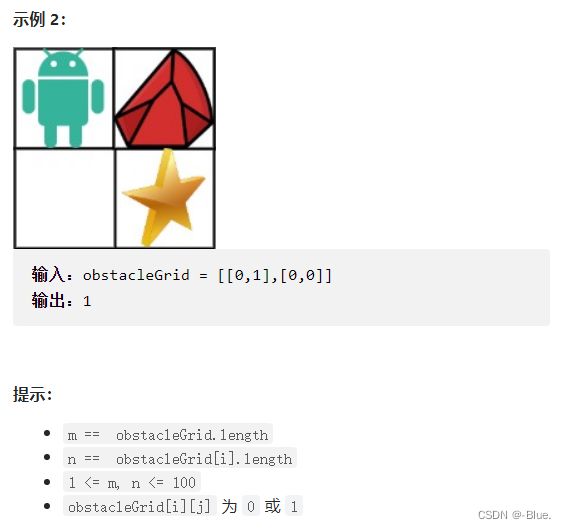
63. 不同路径 II

力扣

动态规划

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        /*
            1. 确定dp数组下标含义—— 到dp[i][j]有几种路径 
            2. 递推公式 —— dp[i][j] = dp[i][j-1] + dp[i-1][j]
            3. 初始化 —— dp[][] 循环初始化，遇见障碍物，跳出，后边都为0
            4. 遍历顺序 —— 从前到后，一层一层
            5. 推导结果
        */
        int m = obstacleGrid.length, n = obstacleGrid[0].length;
        int[][] dp = new int[m][n];
        for(int i=0; i<m && obstacleGrid[i][0]==0; ++i){
            dp[i][0] = 1;
        }
        for(int i=0; i<n && obstacleGrid[0][i]==0; ++i){
            dp[0][i] = 1;
        }
        for(int i=1; i<m; ++i){
            for(int j=1; j<n; ++j){
                if(obstacleGrid[i][j]==1){
                    continue;
                }
                dp[i][j] = dp[i][j-1] + dp[i-1][j];
            }
        }
        return dp[m-1][n-1];

    }
}

343. 整数拆分

力扣

1、动态规划

class Solution {
    public int integerBreak(int n) {
        /*
            1. 确定dp数组下标含义—— 数字i得到的最大乘积dp[i]
            2. 递推公式 —— dp[i] = max({dp[i], (i - j) * j, dp[i - j] * j});
            3. 初始化 —— dp[2]=1 ， dp[3]=2
            4. 遍历顺序 —— 从前到后  外边i从3开始。就从1
            5. 推导结果
        */
        int[] dp = new int[n+1];
        dp[2] = 1;
        for(int i=3; i<=n; ++i){
            for(int j=1; j<=i-j; ++j){
                dp[i] = Math.max(dp[i], Math.max(j*(i-j), j*dp[i-j]));
            }
        }
        return dp[n];
    }
}

2、以因子3等分

class Solution {
    public int integerBreak(int n) {
        /*
            以因子3等分，即分成多个3：
                余数为0 —— 3 的a次方
                1 —— 3的a-1次方 * 4
                2 —— 3的a次方 * 2
        */
        if(n<=3) return n-1;
        int a = n /3, b = n % 3;
        if(b == 0) return (int)Math.pow(3, a);
        if(b == 1) return (int)Math.pow(3, a-1) *4;
        return (int)Math.pow(3, a) * 2;
    }
}

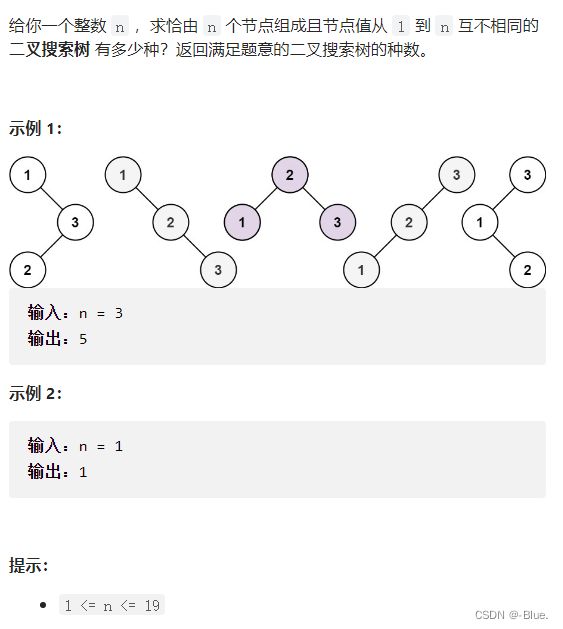
96. 不同的二叉搜索树

力扣

卡特兰数

class Solution {
    public int numTrees(int n) {
        // 卡特兰数
        int[] dp = new int[n+1];
        dp[0] = 1;
        dp[1] = 1;
        for(int i=2; i<=n; ++i){
            for(int j=1; j<=i; ++j){
                dp[i] += dp[j-1] * dp[i -j];
            }
        }
        return dp[n];
    }
}