数据结构——栈和队列

  经过三天悠哉游哉地的学习，终于把栈和队列搞定了。出发之前，永远是梦想；出发之后，永远是挑战。

 

我宁愿做错，也不愿什么都不做。

 

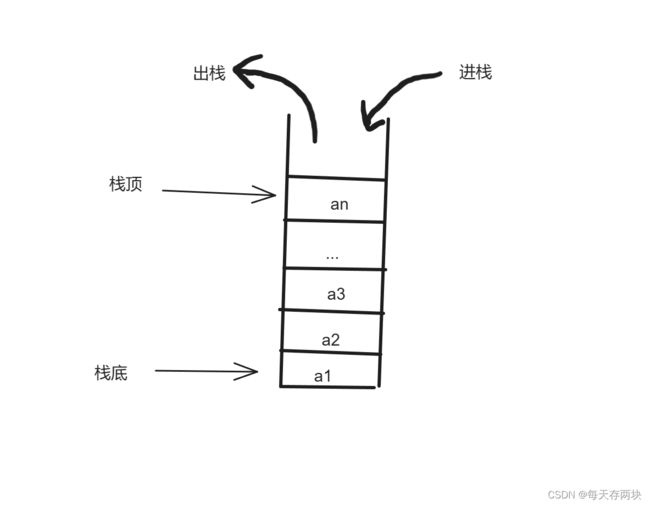
限定性线性表---栈

栈的定义：栈是一种常见的数据结构，它遵循先进后出（LIFO）的原则。栈由一系列元素组成，可以进行两种基本操作：压入（push）和弹出（pop）。压入操作将元素添加到栈的顶部，弹出操作则将栈顶的元素移除。

  在栈中，只能访问栈顶的元素，其他元素都无法直接访问。栈的一个典型应用是函数调用的过程中，函数的局部变量和返回地址都存储在栈中。

 

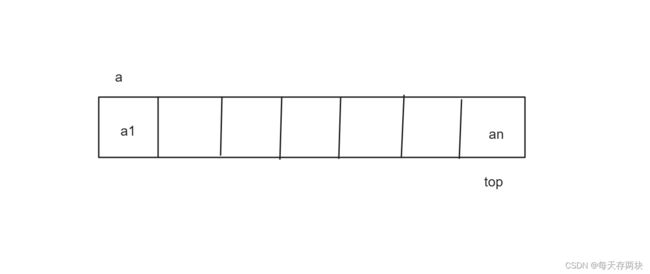
栈可以使用数组或链表实现，具体的实现方式有很多种。 以下是用c语言数组方式实现。

栈的创建

  栈用数组实现的话，只需将顺序表中的size换成top即可。少了一些功能，只让一端进一段出就可以实现栈的特性。这里便让顺序表尾插尾删就行。

typedef int MyType;

typedef struct Stack {
	MyType* a;
	int top;
	int capacity;
}Stack;

 

初始化和销毁栈

//初始化栈
void StackInit(Stack* ps) {
	assert(ps);

	ps->a = NULL;
	ps->top =0;
	ps->capacity = 0;
}
//摧毁栈
void StackDestroy(Stack* ps) {
	assert(ps);

	free(ps->a);
	ps->a = NULL;
	ps->top = ps->capacity = 0;
}

 查空。c语言中要用bool类型，需要引入

bool StackEmpty(Stack* ps) {
	assert(ps);
	return ps->top == 0;
}

 插入元素（压栈）

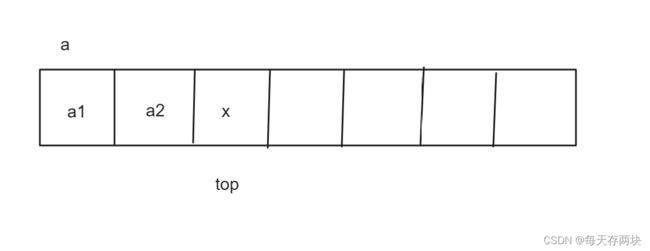
由于是动态数组，所以当空间满时需要增容。

//插入数据
void StackPush(Stack* ps, MyType x) {
	assert(ps);
	//增容
	if (ps->top == ps->capacity) {
		int newCapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;
		MyType* temp=(MyType*)realloc(ps->a, sizeof(MyType) * newCapacity);
		if (temp == NULL) {
			printf("realloc frustration\n");
			exit(-1);
		}
		ps->a = temp;
		ps->capacity = newCapacity;

	}
	ps->a[ps->top] = x;
	ps->top++;

}

 

 删除元素（出栈）

书上的代码是将x返回出去，这里就直接跳过了。

//删除栈顶元素
void StackPop(Stack* ps) {
	assert(ps);
	assert(!StackEmpty(ps));
	ps->top--;
}

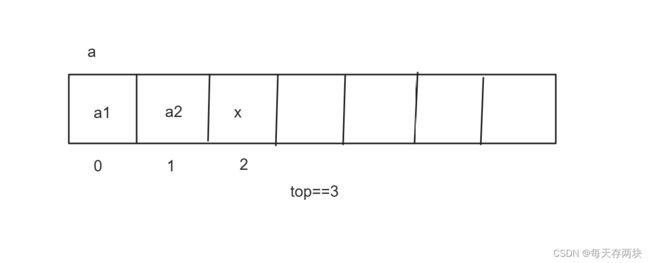
 返回栈顶元素：因为top是从0开始，所以栈顶元素为top-1；

//查找栈顶元素
MyType StackTop(Stack* ps) {
	assert(ps);
	assert(!StackEmpty(ps));
	return ps->a[ps->top-1];

}

 

 一般这种删除，查找操作都需要判断是否为空。

 栈内元素个数：直接就是top个啊。

int StackSize(Stack* ps) {
	assert(ps);
	return ps->top;
}

 

当然后面还有什么双端顺序栈，链栈。原理大致相同，我只简单的了解一下。还有许多无尽的知识，例如栈与递归的实现，阿克曼函数，汉诺塔问题，还有经典的括号匹配问题。

最近看六级作文中有句话是这么说的，there are more knowledges you have,there is you realize how little you know. 意思是你学的知识越多，你就会意识到你知道的越少。

比如以前我只知道用二维数组实现杨辉三角，现在可以用队列实现。

 

队列

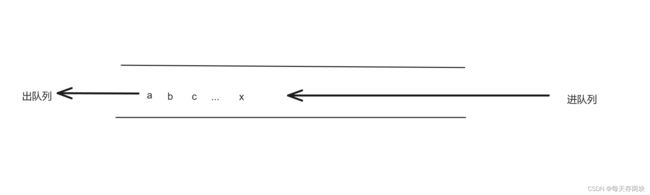
队列的定义：队列是一种常见的数据结构，它遵循先进先出（FIFO）的原则。队列由一系列元素组成，可以进行两种基本操作：入队（enqueue）和出队（dequeue）。入队操作将元素添加到队列的尾部，出队操作则将队列头部的元素移除。

   在队列中，只能访问队列头部的元素，其他元素都无法直接访问。队列的一个典型应用是任务调度，比如操作系统中的进程调度，新任务进入队列的尾部，而正在运行的任务则从队列头部被选取执行。

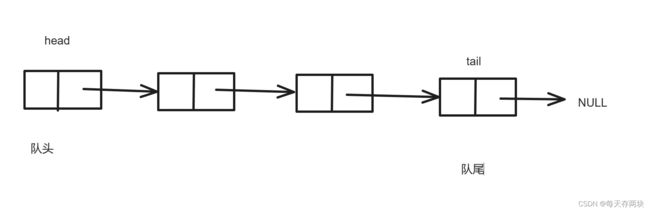
队列可以使用数组或链表实现，具体的实现方式有很多种。以下用单链表实现，因为数组队首出数据，需要挪动后面一大块数据相对麻烦，所以可以用链表的头删实现了出队列。

队列的创建

由于需要一个队尾指针方便插入数据，所以可以用一个结构体包含head 和tail指针，这样对队列节点进行操作时，也只需要传一级指针了。

typedef int MyType;

typedef struct QueueNode {
	MyType data;
	struct QueueNode* next;
}QNode;

typedef struct Queue {
	QNode* head;
	QNode* tail;
}queue;

 

 

初始化和销毁队列 

销毁队列时，需要将所有的节点都释放。

//队列初始化
void QueueInit(queue* pq) {
	assert(pq);
	pq->head = NULL;
	pq->tail = NULL;
}
//销毁队列
void QueueDestroy(queue* pq) {
	assert(pq);
	QNode* cur = pq->head;
	while (cur) {
		QNode* next = cur->next;
		free(cur);
		cur = next;
	}
}

查空：

bool QueueEmpty(queue* pq) {
	assert(pq);
	return pq->head == NULL;
}

 插入元素（入队）

void QueuePush(queue* pq, MyType x) {
	assert(pq);
	QNode* newnode=(QNode*)malloc(sizeof(QNode));
	newnode->data = x;
	newnode->next = NULL;
	if (pq->head == NULL) {
		pq->head = newnode;
		pq->tail = newnode;
	}
	else {
		pq->tail->next = newnode;
		pq->tail = newnode;
	}

}

删除元素（出队）

//删除元素
void QueuePop(queue* pq) {
	assert(pq);
	assert(!QueueEmpty(pq));

	QNode* del = pq->head;
	pq->head = pq->head->next;
	free(del);
	del = NULL;
	if (pq->head == NULL) {
		pq->tail = NULL;
	}
}

队首、队尾元素及队列元素个数：

//队首元素
MyType QueueFront(queue* pq) {
	assert(pq);
	assert(!QueueEmpty(pq));

	return pq->head->data;
}
//队尾元素
MyType QueueTail(queue* pq) {
	assert(pq);
	assert(!QueueEmpty(pq));

	return pq->tail->data;
}
//队列元素个数
int QueueSize(queue* pq) {
	assert(pq);
	assert(!QueueEmpty(pq));

	int count = 0;
	QNode* cur = pq->head;
	while (cur) {
		++count;
		cur = cur->next;
	}
	return count;
}

这样就简单地实现了一个队列。

循环队列

  循环队列是一种使用数组实现的队列，它通过循环利用数组空间来解决普通队列中空间浪费的问题。在循环队列中，数组的首尾是相连的，形成了一个循环。

  具体实现方式是使用两个指针，一个指向队列的头部，称为队头（front），另一个指向队列的尾部的下一个位置，称为队尾（rear）。

  当入队（enqueue）操作时，元素添加到队尾，并将队尾指针后移。如果队列满了，则无法再添加元素。当出队（dequeue）操作时，移除队头元素，并将队头指针后移。如果队列为空，则无法执行出队操作。

  利用循环队列的特点，即队列尾部的下一个位置是队头的位置，可以让队列的元素循环利用数组的空间，减少了空间的浪费。循环队列在实现上需要注意队空和队满的判断条件，并且需要特殊处理队尾指针的移动操作。

 

 如果指针到队尾，只需要+1模上队列长度。

#define QUEUE_SIZE 10 // 定义循环队列的大小
int queue[QUEUE_SIZE]; // 定义循环队列的数组
int front = 0, rear = 0; // 定义队头和队尾指针

// 入队操作
void enqueue(int data) {
    if ((rear + 1) % QUEUE_SIZE == front) { // 队满判断
        printf("Queue is full.\n");
        return;
    }
    queue[rear] = data;
    rear = (rear + 1) % QUEUE_SIZE; // 队尾指针后移
}

// 出队操作
int dequeue() {
    if (front == rear) { // 队空判断
        printf("Queue is empty.\n");
        return -1;
    }
    int data = queue[front];
    front = (front + 1) % QUEUE_SIZE; // 队头指针后移
    return data;
}

 书接上文，如何用队列实现杨辉三角。

 队列实现杨辉三角

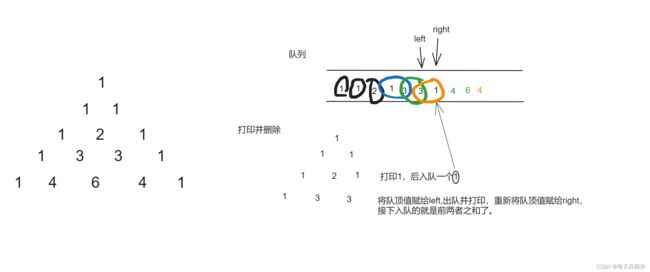
杨辉三角（Pascal’s Triangle）是一个经典的数学图形，由数字构成的三角形。它的第一行只有一个元素1，接下来的每一行都从左到右逐渐增加，每个元素是它上方两个元素的和。

 

 在杨辉三角中，每一行的元素均可以由组合数计算得到，例如第n行第k个元素可以表示为C(n, k)，即从n个元素中选取k个元素的组合数。

思路：

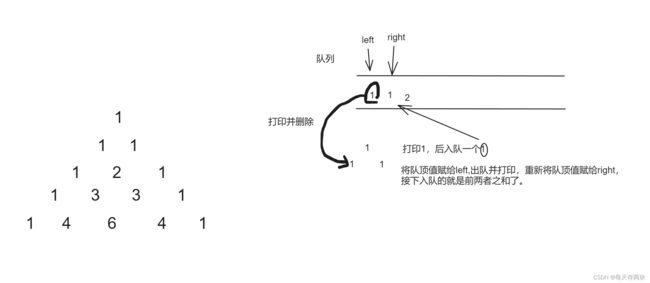
1.每行杨辉三角的起始和末尾都有1，先让第一行的1入队，以后每打印一行结尾就打印一个1并换行，再入队一个1.

 

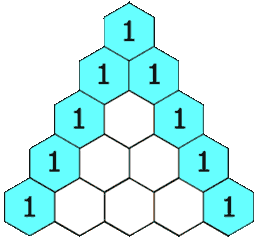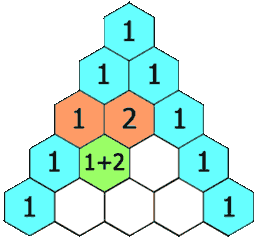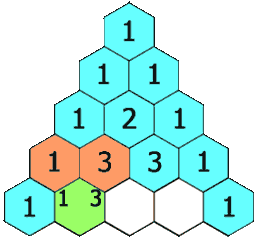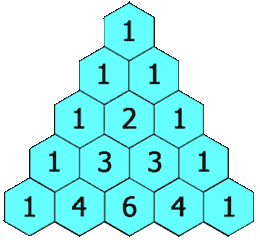
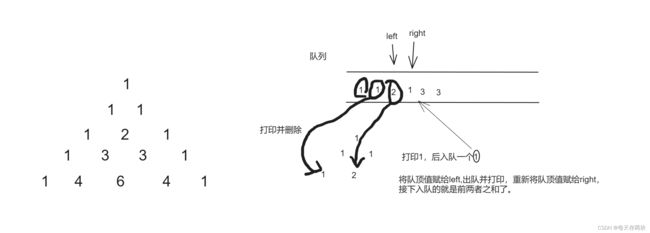
 2.将队顶值赋给left,出队并打印，重新将队顶值赋给right，接下入队的就是前两者之和（left+right）了。

 

 接下来就以此类推：

第3行，需要进行2次入队分别是3，3

 第4行，需要进行3次入队分别是4，6，4

这样假设有n层，每层就需要进行n-1次添加元素， 添加完成后，打印1换行，入队1，无限迭代下去，代码只需要两个for循环就搞定了。下面是用C++队列实现杨辉三角。

#include 
#include 
using namespace std;

int main() {
	queue Yanghui;
	Yanghui.push(1);
	int n;
	cin >> n;
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < i; j++) {
			int left = Yanghui.front();
			Yanghui.pop();
			cout << left<<' ';
			int right = Yanghui.front();
			Yanghui.push(left + right);

		}

		cout << 1 << endl;
		Yanghui.push(1);
	}
	return 0;
}

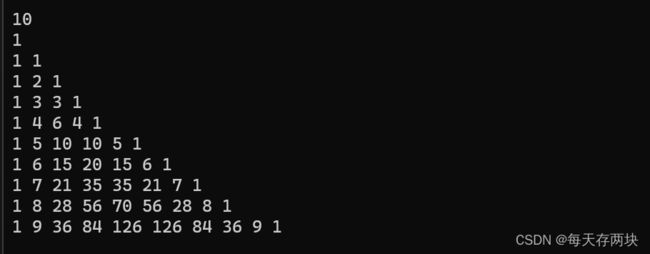
运行结果：

 

今天的总结就到这里了。知识的巩固需要不断温习和刷题，希望我们都能成为想成为那样的人。