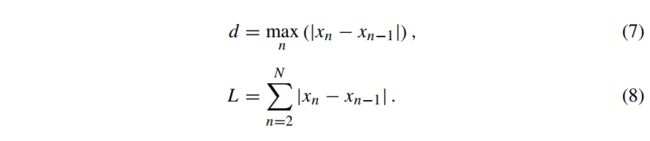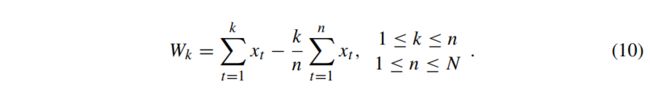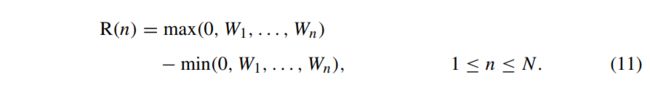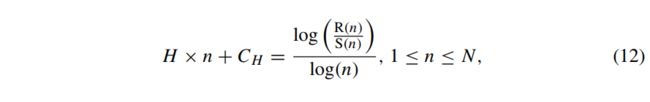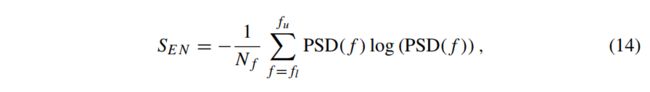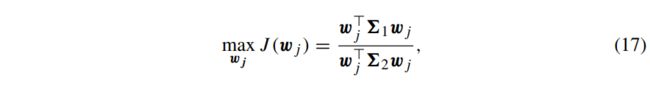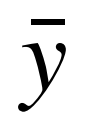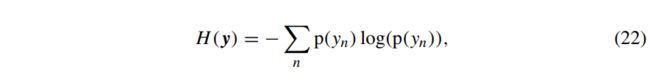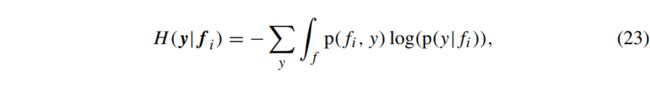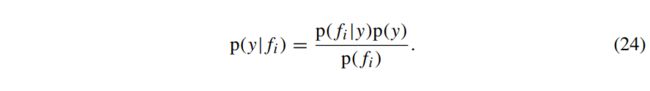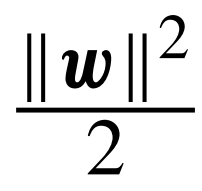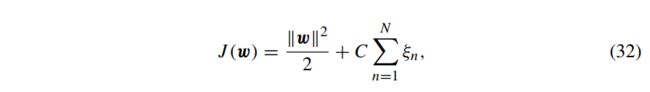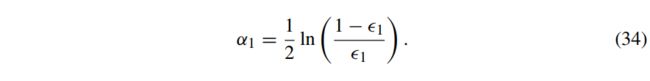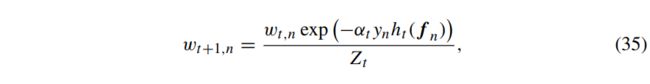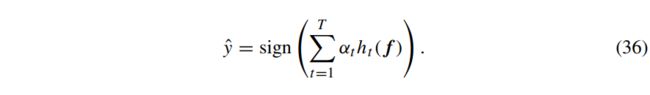脑电机器学习：理论与应用

导读

EEG是一种广泛用于研究记录和监测脑电活动的方法。已经开发了机器学习算法来从EEG中提取信息，以帮助诊断多种疾病(例如癫痫、阿尔茨海默症和精神分裂症)，并识别各种大脑状态。尽管机器学习算法在神经科学中具有精妙且易于使用的特性，但如果执行不当，可能会产生不准确甚至错误的结果。本文概述了基于EEG的机器学习、模式识别和分类的一般方法。首先，描述了从各个领域提取的特征。其次，概述了监督和无监督特征降维方法。重点关注分类算法、性能评估和防止过拟合的方法。最后，讨论了基于EEG机器学习的两个应用：脑机接口(BCI)和微睡眠的检测与预测。

前言

EEG是一种非侵入性方法，可通过头皮上的电极直接测量神经活动。大量神经元的同步活动会产生一个强到足以到达头皮的电场，这被记录为具有高时间分辨率的脑电图。与其他神经成像方法(如fMRI和fNIRS)相比，直接记录神经活动是EEG的优势之一。此外，由于EEG具有高时间分辨率，可以捕获大范围的神经振荡。这些节律分为五个标准波段：δ(0.5-4Hz)、θ(4-8Hz)、α(8-12Hz)、β(13-30Hz)和γ(＞30Hz)。研究表明，每个频段的大脑活动与不同的认知功能有关。这些优点使EEG不仅可以研究神经工程和神经科学中的重要问题，而且是临床应用和疾病诊断过程中的一种可行和实用的选择。

EEG信号包含有关空间、时间和频谱方面的大量信息。这使得EEG成为研究大脑功能和认知等方面的合适方法。然而，EEG的丰富性是有代价的，其中数据可能是高维的，并且可能具有低信噪比，这对处理EEG和识别感兴趣的模式提出了相当大的挑战。为了解决EEG固有的挑战，机器学习在该领域得到了相当多的关注。

EEG通常受到噪声和伪影的影响，如眼动、慢漂移和肌肉伪影。为了提高信噪比，通常包括预处理步骤，都会最大限度地减少伪迹和不必要的噪声。该步骤可以包括各种程序，例如带通滤波、伪影子空间重建、独立成分分析、空间滤波器、最小化肌肉伪影和伪影拒绝。然而，在预处理中，必须谨慎并可视化数据，以避免去除任何有意义和信息丰富的EEG成分。

机器学习

机器学习是一组算法，使我们能够自动识别数据中的模式，并对新观察到的测量值进行预测。在神经科学研究领域中，通常会出现这些情况：①对比各种条件，②诊断疾病，③识别与行为相关的电生理变化。尽管具体应用不同，但机器学习的过程在大多数情况下是相似的，如图1所示。

图1.基于EEG的机器学习的概览图。

一般来说，机器学习有两个阶段：训练和测试。在训练阶段，有一组可用的示例(即带有相应标签的数据)。使用给定的机器学习算法，示例数据被用于训练模型(即调整其参数)，以便它可以识别输入数据和标签之间的关系。在测试阶段，没有标签的输入数据经过与训练阶段相同的方法进行预处理、特征提取和特征约简，训练阶段估计的训练模型预测输出(即标签)。训练阶段的主要目标是估计在测试时具有最大预测性能的模型。

特征提取

特征提取是指通过测量和提取特定信息来降低输入数据维数的一套方法。对于EEG数据，有多种方法可以从时域、频域或空间域的一个或组合中提取特征。

①时域特征

EEG信号的时域特征提取无需任何变换。过零是一种时域特征，表示信号越过零的次数。该测量方法和过零间隔已用于癫痫检测、情绪识别和睡眠分期。

Hjorth参数是描述EEG单通道的三个时域特征集。这些特征是活动性、移动性和复杂度。Hjorth活动性(HA)是EEG信号的方差(即信号功率)，表示信号的宽度。Hjorth移动性(HM)估计信号的平均频率。Hjorth复杂度(HC)通过计算EEG的一阶导数相对于EEG本身的移动性来估计EEG信号的带宽。Hjorth参数可以计算为：

其中σ0是信号的标准差，σ1和σ2是信号的一阶和二阶导数的标准差。Hjorth参数已用于睡眠分期、情绪识别和癫痫检测。

非线性能量，也称为平均Teager能量，是EEG的一个特征，已被广泛用于癫痫发作预测。非线性能量估计信号的瞬时能量，特别是识别瞬态变化，如睡眠纺锤波和发作尖峰。它还被用于自动睡眠分期，在这方面它是最重要的功能之一。假设时域信号用x={x1,x2,...,xN}表示，计算的非线性能量为：

分形维数是不同尺度上的自相似性度量，常用于量化信号或过程的复杂性。由于估计复杂信号的分形维数存在计算上的挑战，目前已经开发了几种方法来近似分形维数。Petrosian分形维数是分形维数的最简单近似。Petrosian分形维数特征通过将信号转换为二进制表示，并用符号变化的次数近似分形维数来简化分形维数的计算：

其中NEEG是EEG信号的采样点数，NΔ是信号的符号变化数。Petrosian分形维数已用于检测嗜睡水平和估计睡眠阶段。

Katz分形维数是估计信号分形维数的另一种方法。该方法比Petrosian分形维数更精确，但计算成本更高。Katz分形维数计算为：

其中NEEG为EEG信号点的数量，d为直径，L为曲线长度。假设x=x1,x2,...,xNEEG是EEG信号的序列，则直径和曲线长度分别为：

Katz分形维数已用于阿尔茨海默症的诊断、精神分裂症的诊断以及嗜睡水平的估计等。

平均曲线(线)长度是Katz分形维数的近似值。令x={x1,x2,...,xN}为EEG信号，平均曲线长度的计算公式为：

曲线长度已被用于预测癫痫发作和估计睡眠的不同阶段。

Hurst指数是时间序列中的长程自相似性度量。Hurst指数可以取0到1之间的值，其中值0.5对应随机数据。为了计算Hurst指数，假设信号由x={x1,x2,...,xN}给出。前k个数据点与前n个数据点均值的偏差由下式得到：

范围R(n)定义为前n个点的偏差之间的最大差值：

Hurst指数为：

其中CH是独立于n的有限常数，S(n)是前n个点的经验标准差。Hurst指数可以通过在(12)的右侧拟合一条直线来计算。Hurst指数已被用于识别癫痫样EEG，识别情绪和估计睡眠阶段。

②频域特征

从EEG信号的频率表征中提取频域特征。快速傅里叶变换(FFT)是EEG信号频率分量识别的常用方法，由下式得到：

其中f为频率，N为信号中的总点数，xn为第N个信号点，Ts为采样时间。信号的频率分量可以测量到Nyquist频率(即采样频率Fs的一半)。此外，对于长度为N的信号，可以计算从0到Nyquist频率均匀分布的

个频率分量，即

例如，采样频率为250Hz的4s EEG片段的频率分辨率为

从这个例子中可以清楚地看出，频率分辨率取决于信号的长度，与采样频率无关。傅里叶变换的一个假设是信号是平稳的，这意味着信号的统计量(例如，均值和标准差)不随时间变化。然而，EEG反映的是大脑功能的动态，其本质上是非平稳的。解决此问题的一种方法是将FFT应用于相当平稳的EEG片段。尽管如此，但这种方法仍然会降低结果的频率分辨率。此外，为了减少频谱泄漏，在计算FFT之前，需要对信号应用一个加窗函数，例如汉明窗或汉宁窗。

还有其他信号处理方法可以量化频率分量和执行频谱分析，例如小波变换，希尔伯特变换和匹配追踪。这些方法通常用于识别数据的时频表征。接下来将重点介绍从信号的频域表征中提取特征。

功率谱密度估计给定信号中功率在频率分量上的分布。Welch方法，也称为修正周期图法，是一种应用广泛的功率谱密度估计方法。Welch方法(修正周期图法)通过对重叠较小加窗段的周期图进行平均来计算信号的功率谱密度，因此与整个epoch的周期图相比，该方法的方差较小。功率谱密度已被用于检测和预测微睡眠、识别阿尔茨海默症的幻觉、估计睡眠阶段和预测嗜睡。

频谱熵表征EEG的复杂性或规律性。为了计算频谱熵，信号的概率分布近似于其功率谱密度。然后由下式计算频谱熵：

其中Nf为频率箱的数量，fl和fu分别为频率下限和上限。频谱熵已被用于对精神分裂症患者进行分类，检测癫痫发作，并估计睡眠阶段。

强度加权平均频率(IWMF)，也称为重力频率，通过下式计算信号相对于功率谱密度的加权平均频率：

强度加权带宽(IWBW)，也称为频率变异性，定义为频率的方差。使用IWMF和频谱密度，IWBW的计算公式为：

IWMF和IWBW均已用于检测嗜睡和癫痫发作。

③空间域特征

共空间模式(CSP)是一种从多通道EEG信号中提取特征的监督算法。这是一种数据驱动的方法，旨在找到EEG信号的分解，使新空间中两种条件之间的距离最大化。设Xk={Xk,1,Xk,2,...,Xk,Nk}为条件k∈{1，2}下的所有EEG段。CSP的目标是找到一组J空间滤波器W={w1,w2,...,wJ}，将EEG信号投影到两种条件之间距离最大的新空间中。对于每个空间滤波器，则有：

其中Σk∈{1，2}是第k个条件下的协方差矩阵，‖wj‖=1，空间滤波器正交。协方差矩阵可以计算为：

求解(17)等价于求解广义特征值问题。在Matlab中，这可以简单地通过W=eig(Σ1，Σ1+Σ2)来找到最佳空间滤波器。然后使用这些滤波器将EEG数据投影到新空间中，即使用空间滤波器乘以EEG数据(WX)。投影信号的方差(或对数变换)被提取为特征。

滤波器组CSP(FBCSP)是经典CSP的扩展，首先将输入数据过滤到不同的频段，然后为每个频带中的数据找到一个CSP。尽管与经典的CSP相比，FBCSP表现出了优越的性能，但由于它生成了大量的特征，因此更有可能导致过拟合。

CSP的一个缺点是它容易受到噪声的影响，这可能导致过拟合。为了克服这个问题，有研究开发了不同的方法。其中一种方法是通过加入正则化项来惩罚模型的复杂度。这些方法试图通过降低复杂度来优化CSP的性能和通用性。贝叶斯框架也被研究纳入稀疏先验自动选择空间滤波器的最佳数量。还有一些方法执行特征选择技术，迭代地选择最佳滤波器数量。

特征降维

从EEG数据中提取的特征通常具有高维数。例如，可以将采集自60个电极的EEG过滤为0-80Hz的2Hz子带，并为每个电极和子带提取3个特征。总共有3×60×40=7200个特征，这可能超过观测值的数量。在机器学习中，这被称为维度诅咒，可能导致过拟合。当一个模型过拟合时，它可以准确地识别它所见过的示例，但它在新的和之前未见过的观测值上表现不佳。

特征降维旨在通过减少预测模型中使用的特征数量来提高机器学习模型的可泛化性。此外，特征降维可以更好地理解科学问题的潜在神经过程。特征降维分为两大类：有监督和无监督。

①无监督

无监督特征降维是指在不使用训练数据标签的情况下减少特征数量的技术。一般来说，减少特征数量的方法有两种：特征选择和特征变换。在特征选择中，选择输入特征的子集，而在 特征变换中，简化的特征(即元特征)是输入数据的低秩近似。

已经开发了几种无监督特征降维方法。Mitra等人开发了一种选择特征以减少冗余的方法。类似地，Singh等人开发了一种基于排名的特征选择(FSULR)的无监督学习，以消除冗余特征。特征变换方法，如独立成分分析(ICA)、主成分分析(PCA)和t分布随机邻域嵌入(t-SNE)等已用于特征降维。这里将重点关注PCA，这是一种广泛用于执行无监督特征降维的技术。

PCA是一种线性特征降维方法，将相关特征分解为不相关的主成分(潜在变量或元特征)。形式上，设X∈RN×D是具有N个观测值的特征矩阵，每个观测值都有D个特征。PCA旨在线性投影数据，则有：

其中W∈RL×D为载荷矩阵，Z为潜在变量(元特征)的矩阵。PCA假设载荷矩阵W是正交的(即，WW⊤=I)。为了找到载荷矩阵，可以对特征矩阵

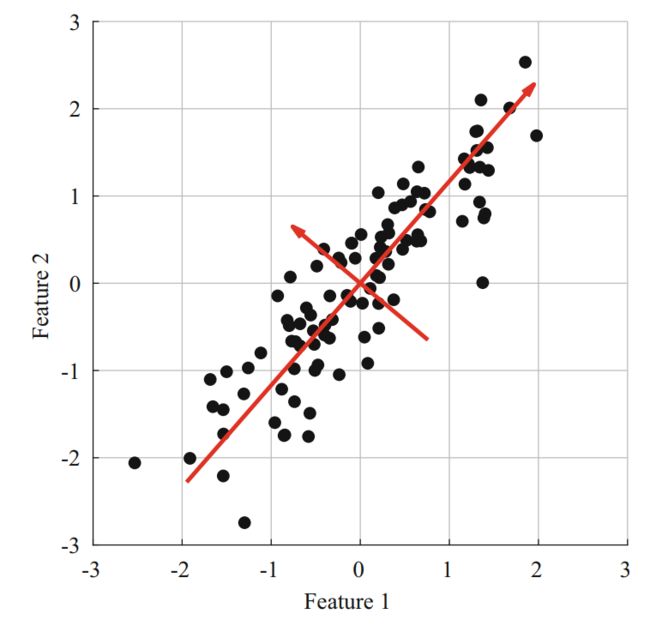
的协方差进行特征值分解。然后将元特征计算为原始特征在协方差矩阵特征向量上的投影，如图2所示。为了降低特征的维数，保留与较高特征值对应的主要特征向量，并丢弃其余的特征向量。这些成分将解释原始特征矩阵中的大部分方差。然而，对于保留的主成分应该解释多少差异，尚未达成共识。一些研究人员使用固定值(例如95%)作为临界值，而另一些研究人员则选择预定义数量的成分(例如十个成分)。另一种选择最佳成分数量的方法是使用交叉验证法。

图2.使用PCA在两个相关特征上查找不相关的元特征。红线对应协方差矩阵的主方向(特征向量的方向)。

PCA是一种强大的特征降维技术，尤其是在处理高维数据时。然而，PCA对数据规模很敏感，这意味着高方差的特征可能会误导PCA。这可以通过在应用PCA之前对特征矩阵进行标准化来解决；也就是说，对于每个特征，删除其均值并除以其标准差。执行PCA后，元特征(即转换后的特征)将用于分类步骤。

为了克服PCA的缺点，已经开发了其他的PCA变体。核主成分分析(KPCA)是对主成分分析进行非线性特征降维的一种扩展。概率主成分分析(PPCA)是以概率生成模型的形式重新表述PCA。与PCA相比，PPCA的一个优点是它为观测数据显式地建立了加性高斯噪声模型。PCA的贝叶斯变体也被开发来合并稀疏性增强先验(例如，自动相关性确定)，以自动识别最佳成分数量。

②监督

监督特征降维技术在减少特征数量时利用结果标签(分类或连续)。特征选择包含了大多数有监督的特征降维方法，在这种方法中，选择相关特征的子集，丢弃冗余和不相关的特征。特征选择方法可以分为三类：过滤器、包装器和嵌入式方法。

过滤器方法使用一种秩函数，根据特征与结果标签的相关性对特征进行评分。过滤器方法计算效率高，可降低过拟合的倾向。有不同的秩函数来估计特征的相关性，例如相关和互信息。然后为预测模型选择最相关的特征。

相关系数通常用于对特征进行排序，衡量两个随机变量之间的线性关联程度。它的值在-1和1之间，分别对应完全负相关和完全正相关。相关性为0表示没有线性关联。形式上，设fi∈RN为特征i对应的向量，y∈RN为N个观测值的结果标签(即黄金标准)向量。皮尔逊相关系数可以计算为：

其中

和

分别是特征i和结果标签的平均值。皮尔逊相关性容易受到异常值的影响，当应用于有噪声的数据时，可能会获得较差的结果。为了缓解这一问题，可以使用皮尔逊相关的非参数版本斯皮尔曼相关。斯皮尔曼相关首先对数据进行排序，然后计算排序后的数据的相关系数。对数据进行排序可以在不删除异常值的情况下消除异常值带来的影响，因此，斯皮尔曼相关不太容易受到异常值的影响。

互信息测量两个变量之间的依赖关系。互信息的值为0表示两个变量是独立的，而正值表示两个变量之间的依赖程度。从形式上讲，互信息可以计算为:

其中fi和y分别对应于两个变量(即第i个特征向量和结果标签)，H(x)为变量x的熵，H(x|y)为给定y条件下x的条件熵。结果标签y的熵由下式得到：

其中p(x)为离散变量x的概率质量函数。当x连续时，(22)中的求和被积分取代，p(x)成为概率密度函数。在给定结果标签的情况下，特征i的条件熵由下式计算：

其中，使用贝叶斯法则，给定特征i的结果的条件概率为：

给定特征i和结果标签的概率函数，可以使用(22)-(24)计算两个变量的互信息。然而，这些变量的概率分布不是先验已知的，因此需要从数据中估计。一种方法是将特征i的观测值拟合为高斯分布，这等效于根据数据经验估计的平均值和标准差的正态分布。该方法对于正态分布的特征计算快速且高效，但无法准确建模非正态分布的数据或具有多模态分布的数据。在这种情况下，可以使用高斯混合模型或核密度估计来估计数据的概率分布，其精度较高，但这些模型计算复杂度较高，计算时间也较长。

包装器方法使用分类或回归方法来迭代地选择特征。这些技术根据机器学习算法的性能查找特征的子集。包装器方法一般分为前向选择和后向消除两大类。在前向选择中，每个特征首先分别用于训练分类(或回归)模型。选择性能最高(或误差最低)的特征。然后，将最佳特征和另一个特征结合起来训练另一个模型。选择性能最高的特征组合。此过程一直持续到满足停止标准为止。这可以是预先选择的特征数量，对感兴趣的性能测量的预定义阈值(例如，90%的准确率)，或者在迭代过程中的性能改进(例如，0.1%的改进)。后向消除实现了类似的想法，但从所有的特征开始。在每次迭代中，都会消除一个特征并评估性能。消除对性能影响最小的特征。

嵌入式方法是在训练阶段实现的，在参数值估计过程中选择特征。例如，使用L1范数正则化分类算法在训练阶段将不相关特征的系数缩小为零。这基本上从最终的预测模型中删除了不相关和冗余的特征。

分类算法

分类器学习如何在训练阶段和根据训练数据(包含特征及其相应的分类标签)进行预测。在训练阶段之后，分类器可以对新的未知数据进行预测。当手头的问题具有连续的结果时，使用回归方法来识别训练数据中的模式。当结果标签可以取两个唯一值(例如阿尔茨海默病的诊断)时，分类问题是二元的。在多类分类问题中，结果标签具有两种以上的状态，例如睡眠分期，情绪识别和BCI。

①线性判别分析

线性判别分析(LDA)的目标是找到一个能最大限度地分离不同类特征的超平面。LDA是一种生成分类器，它假设每个类的数据是正态分布的，并且两个类的数据具有相同的协方差矩阵。假设Fk∈RNk×D是第k类(即，k∈{1，2})的特征矩阵。LDA的均值和协方差矩阵可计算为：

其中fn,k是一个列向量，对应于第k类的第n个观测值的特征。由于这里重点关注二元结果，可以将新的观察结果分类为：

其中Nk是k∈{1，2}类的观测值数，d为负值，则新观测值

属于第一类；d为正值，则对应第二类观测值。

LDA的另一种观点是Fisher判别分析，它旨在最大化类间方差，同时最小化类内方差。这可以写为瑞利商(Rayleigh quotient)，可以通过广义特征值分解来求解。LDA的生成和判别观点都得到了相同的结果。

②支持向量机

支持向量机(SVM)是一个线性分类器，用于查找两个类的数据之间的超平面。支持向量机是一种最大边界分类器，这意味着决策边界的确定使决策超平面与其周围数据点之间的裕度最大化，如图3所示。

图3.线性SVM分类器的决策边界(黑线)及其裕度。蓝点和红方块分别对应两个类的数据。

找到与两类数据距离最大的决策边界可降低错误分类的可能性。最接近决策边界的数据点称为支持向量。这些支持向量对决策边界的影响最大。

假设fn∈RD为第n次观测的特征向量，其对应的结果标签为yn∈{−1，1}。对于没有最大化边界的分类器(如LDA)，最优边界由下式给出：

其中w是权重向量，b是偏差项。假设数据是线性可分的，SVM的最佳边界为：

这将使训练阶段的边界最大化。但是，一个较大的权向量w可以满足此约束。因此，SVM的目标函数是最小化

，受(29)给出的约束。这种优化可以用二次规划来完成。SVM的测试阶段与LDA的测试阶段相似。给定一个测试数据点

，通过以下计算实现SVM的预测：

其中

是预测的类，sign(x)是符号函数。

然而，在大多数实际应用中，数据不是线性可分的。在这种情况下，不存在完美的决策边界，分类器至少会犯一个错误。因此，目标是找到一个具有最高精度的决策边界。这是通过添加松弛变量ξn≥0来完成的，以说明每个观测值的分类误差。当一个观测值是正确的且具有高边界时，其相关松弛变量为零。但是，当松弛变量的相关观测值落在边界内或被错误分类时，松弛变量的值会增加。在(31)中加入松弛变量得到：

与线性可分数据的情况类似，需要一个目标函数。为了合并松弛变量(误差项)，最小化的目标函数由下式得到：

其中C＞0是一个正则化参数，用于控制误差项和边界之间的平衡。C的值较大，可查找较小的裕度以减少训练误差，而C的值越小，则试图寻找较大的裕度以减少训练误差。

当两类数据间的真实决策边界为非线性时，寻找线性超平面可能导致分类性能较差。在这种情况下，可以使用核技巧将输入数据映射到决策边界为线性的不同空间。然后，线性分类器可以在新空间中以最佳方式找到决策边界。两种最常用的核是径向基函数和多项式。然而，核技巧大大增加了计算复杂度。当处理具有许多观测和特征的大型数据集时，这就成为一个问题。

③k-最近邻

K-最近邻(kNN)是对数据做最小假设的非线性分类器。对于给定的测试观测值，kNN会在训练数据中找出k个与测试观测距离最小的观测值。然后使用这些训练点的多数标签作为测试观测值的预测类。数据点之间的接近度由距离度量来定义，其中欧氏距离是常见的选择。

kNN分类器使用一种简单的方法来预测新观测值的标签，而无需显式建模训练数据。然而，在实际操作中，kNN可能会变得不稳定，特别是在处理EEG等有噪声的数据时。在这种情况下，增加k将改善泛化误差。此外，kNN需要从所有训练数据中计算新的观测结果的距离，计算复杂度很高。

④决策树

决策树是一种简单灵活的分类方法，目前得到了广泛的应用。决策树通过一组形成树形结构的层次规则对观测结果进行分类。基于训练数据形成决策树的算法有CART，ID3，C4.5和C5.0等。决策树在训练阶段执行特征选择，允许在不同规则中多次使用一个特征，并且易于解释。然而，决策树容易过拟合，树的大小可能会过度增长。

⑤集成方法

集成学习是指使用多个分类器进行预测。我们希望实现具有最大性能的分类器，但这可能无法通过单个分类器实现。集成学习的思想是，当多个弱分类器(其各自的性能优于随机分类器)组合在一起时，可以获得更高的性能。集成学习的性能预期要高于单个分类器的性能。三种常用的集成方法是堆叠法、提升法和自助法(bagging)。

堆叠法，也称为堆叠泛化，是一种组合了多个分类器输出的集成方法。首先对基分类器进行独立训练。基分类器也称为弱学习器、弱分类器或基学习器。堆叠法是对多个分类器的输出进行加权平均，使分类性能最大化，可以看作是一种模型平均。与单个分类器相比，堆叠法显示出优越的性能。

提升法是一种迭代方法，它结合了多个弱分类器以创建强大的自适应模型。在提升法的每次迭代中，首先对数据进行加权，以突出显示先前分类器的误差。然后用加权数据来训练一个新的基学习器，旨在校正先前分类器的错误。基学习器可以是任何分类算法。尽管如此，最常用的基学习器是LDA、SVM和决策树。

自助法已在文献中被广泛使用，并开发了不同的自助法变体。使用最广泛的自助法是自适应增强(AdaBoost)。形式上，设F={f1,...,fN}为N个观测值的特征矩阵，设y={y1,...,yN}为相应的结果标签(1或-1)。在第一次迭代中，将每个观测值的初始权值设置为

。使用权向量、特征矩阵和结果标签，训练一个基分类器h1。随后，h1的错误分类误差计算为：

其中h1(fn)是分类器h1对观测值fn的预测。下一步是计算该分类器的权重，由：

此时，第一次迭代完成。对于连续迭代，权向量wt更新如下：

其中Zt是归一化因子。在(35)中可以看出，在计算下一次迭代的权向量时，已经考虑了当前迭代的分类误差。迭代过程继续进行，直到完成预定义数量的迭代T(即，训练T基分类器)。对未知的观测值

进行预测是通过计算分类器输出的加权平均值来完成的，由下式可得：

预测是根据分类精度对基学习器进行加权平均。

AdaBoost的缺点是其过拟合训练数据的倾向。在存在标签噪声的情况下，AdaBoost高度过拟合错误的标签，因为它多次尝试正确分类所有的训练数据。然而，AdaBoost的这一特性已被用于识别和消除带有标签噪声的观测值。

自助法(bagging)也使用混合基分类器来预测观测结果。与按顺序训练基学习器的增强方法不同，bagging对所有分类器执行并行训练。最初，通过引导创建训练数据的多个子集。然后用每个子集训练一个基分类器。在训练阶段之后，每个分类器都用于预测新的未知观测值的标签。最终预测是通过使用基分类器的多数投票来完成的。研究表明，与boosting相比，当数据存在噪声时，bagging更稳健。此外，与boosting相比，bagging对标签噪音的抗噪性更强。

决策树通常用作bagging方法的基分类器。决策树本身是一种简单的方法，具有较高的灵活性，但往往会导致过拟合。然而，在bagging算法中，当使用决策树作为基分类器时，通常可以获得较高的性能。这种组合被称为随机森林。随机森林已被证明具有较高的准确性，并在文献中得到了广泛的应用。

⑥正则化

机器学习的一大挑战是避免过拟合，在这种情况下，机器学习模型可以正确识别已知的所有(或大多数)例子的结果标签，但在估计新的未知观测结果标签时表现很差。因此，训练后的模型对新的观测结果的泛化能力较差。当机器学习算法具有高度的灵活性并能够与训练数据中的噪声密切拟合时，过拟合变得更加明显。降低过拟合可能性的一个重要方法是进行特征降维。

最小化过拟合的一个更明确的方法是使用正则化项。正则化模型的概念在于降低模型的复杂度，从而平滑决策边界并允许在训练阶段出现错误。最常用的正则化是L1和L2范数。对于向量w={w1,...,wK}，Lp范数由：

如果没有正则化项，训练阶段的目标是最小化实际结果标签和估计结果标签之间的误差。这是通过最小化损失函数

来完成的，其中y是实际结果标签，

是使用预测模型G的估计结果，该预测模型使用权向量w来预测特征矩阵F的标签。为了合并正则化，在训练阶段最小化的目标函数J应该是损失函数和正则化项的组合：

其中R(w)是正则化项，λ是用户定义的参数，用于控制模型的复杂度和训练精度之间的平衡。当λ=0时，不应用正则化，(38)中给出的目标函数简化为损失函数。当λ＞0时，目标函数J成为训练精度和决策边界平滑度之间的折衷。λ的值越大，决策边界的平滑度就越重要，而较小的λ值更强调训练样本的正确识别。

交叉验证方法用于选择λ的最佳值。这是通过对不同的λ值执行交叉验证，并选择对应于最高预测性能的值来实现的。在交叉验证中，从整个数据集中选择λ的最佳值可能会导致对预测性能的估计有所偏差。嵌套交叉验证可用于缓解此问题，它是指在另一个交叉验证的训练数据上执行交叉验证。

交叉验证

机器学习算法，无论是分类模型还是回归模型，都需要一组独立的测试数据来评估训练阶段后的预测性能和泛化误差。但是，我们并不总是能够获得一个独立的测试数据集。因此，不仅要利用手头的数据来训练模型，还要评估训练模型的性能和可泛化性。当机器学习模型高度灵活时，这一点变得更加重要。例如，一个k=1的kNN分类器正确分类了所有的训练数据，但决策边界是高度非线性的，并且偏向于训练数据。这个模型在预测新的未知观测结果的正确标签方面可能表现很差。另一方面，当k非常大时，kNN分类器倾向于支持训练观测值数量最多的类，这也可能无法正确预测新观测值的标签，特别是对于高度不平衡的数据集。在这种情况下，可以使用交叉验证来评估训练模型在不同参数下的分类性能，然后选择能够实现最高预测性能的参数。

交叉验证是一种评估模型泛化误差的简单技术。交叉验证将训练数据划分为K个不重叠的分区，其中K-1分区的一个子集用于训练模型，另一个分区用于测试模型。这称为K折交叉验证。在K折交叉验证中，整个训练和测试过程重复K次，这样每个分区都被用作一次测试数据集。然后将模型的总体性能估计为K个模型的预测性能的平均值。通常使用5折和10折交叉验证。留一交叉验证是也常用的方法，当K等于训练观测值数时是一种特殊情况。

在使用交叉验证时必须谨慎，以避免对性能估计产生偏差，例如，当特征降维方法应用于训练数据时。可以基于整个训练数据集应用特征选择，并仅对所选特征应用交叉验证。交叉验证计算该模型的预测性能(即特征选择后)将导致有偏估计，因为测试数据已经用于特征选择。在这种情况下，要执行无偏交叉验证，必须首先将数据划分为K个分区，并留下一个分区进行测试。然后，其余的K-1分区用于执行特征选择，并随后用于训练分类器。重复此过程K次，以实现对分类性能的无偏估计。

如前所述，预测性能的无偏估计需要一个独立的测试数据集。这在处理EEG数据时尤其重要，因为这些数据可能在时间上是相关的。Li等人发现静息-觉醒条件下的EEG动态与执行任务时诱发相关电位的P3成分之间存在被试内相关性。其他研究利用EEG的被试内特征开发基于EEG的指纹和生物识别系统应用。这些研究结果表明，数据中存在EEG的被试特异性特征，甚至来自多个session；因此，来自不同时间点的被试内EEG片段可能不是独立的。因此，在评估与被试无关的模型性能时，对来自多个被试EEG的连接特征执行K折交叉验证可能会导致对性能的有偏估计，这并不能反映真正的泛化误差。为了实现无偏估计，划分被试进行交叉验证是必要的。

性能评估

在训练阶段之后评估机器学习算法的性能时，需要定量的度量。为了评估预测模型性能的各个方面，已经开发了几种度量方法。接下来，将概述常用的性能度量。

混淆矩阵，也称为列联表，是一个包含关于每个类别正确和错误分类数量信息的矩阵。在二元分类问题中，有两个类通常被标识为阳性和阴性；阳性类是感兴趣的类别(例如，癫痫发作)。真阳性是指正确预测了阳性类，而假阳性(I类错误)是指将阴性类错误地预测为阳性类。阴性类的相同概念有真阴性和假阴性(II类错误)。因此，二元问题的混淆矩阵有四个元素，即真阳性(TP)、假阳性(FP)、真阴性(TN)和假阴性(FN)的总数。这些为训练过的模型提供了预测性能的概述。

灵敏度(Sn)，也称为真阳性率或召回率，是正确识别的观测值在阳性类中的比例。同样，特异性(Sp)，也称为真阴性率，是阴性类中正确预测实例的比例。精度(Pr)，也称为阳性预测值，是正确识别的阳性实例相对于阳性预测总数的比例。这些度量可以计算为：

灵敏度度量的是模型在不考虑阴性类预测的情况下预测阳性类的准确性。另一方面，特异性是对模型的阴性类预测能力的度量。相反，模型的特异性和精度都受到假阳性的影响。因此，尽管这些度量值量化了预测模型性能的各个方面，但它们并不能单独提供整体性能。例如，一个完美的精度(即Pr=1)表示模型正确预测了所有阴性类观测值的标签，因此没有假阳性。但是，它没有提供有关模型灵敏度的任何信息。

准确性是一种广泛使用的评估分类模型预测性能的指标。准确性度量的是正确预测的标签与观测值总数之间的比率，计算公式为：

当数据集是平衡的(即阴性观测值和阳性观测值的数量相等时)，0.85的准确性对应于对85%数据标签的正确预测。但是，在估计类不平衡数据集的预测性能时，准确性度量可能具有相当大的误导性。例如，在包含来自阴性类的85个观测值和来自阳性类的15个观测值的数据集中，将所有内容预测为阴性类的分类器仍会显示0.85的高准确性。

F度量是一种作为灵敏度和精度的调和平均数来估计预测性能的度量方法。它可以取0到1之间的值，分别对应于最差和最佳性能，计算公式为：

其中β是一个用户定义的参数，用于调整灵敏度与精度的相对重要性。

几何平均数(GM)是一种基于灵敏度和特异性的性能度量，计算公式为：

phi相关系数，也称为Matthews相关系数，是另一个性能指标，已被广泛用于评估非平衡数据集的性能。其计算公式为：

上述所有度量方法都利用预测标签来估计预测模型在分类器输出的特定阈值下的性能。相比之下，受试者工作特征(ROC)曲线使用阈值化之前分类器的输出，并估计不同阈值下灵敏度和特异性之间的权衡轨迹。通过使用不同的阈值对分类器的输出进行二分类，估计ROC曲线。对于每个阈值，评估灵敏度和假阳性率(即1-Sp)。最后，通过绘制灵敏度与假阳性率的关系来形成ROC曲线(如图4所示)。随机分类器的ROC曲线是将(0，0)的灵敏度和假阳性率与其对应的(1，1)值连接起来的直线(图4中的蓝线)。另一方面，完美分类器对应于ROC曲线上的灵敏度为1，假阳性率为0。ROC曲线下面积(AUC-ROC)通常用作分类器的性能指标。AUC-ROC取0到1之间的值，其中1对应完美分类器，0.5对应于随机分类器，0对应于完全反转分类器。

图4.三种假设分类器的ROC曲线。蓝线对应于随机分类器。绿曲线对应的分类器优于红曲线对应的分类器。

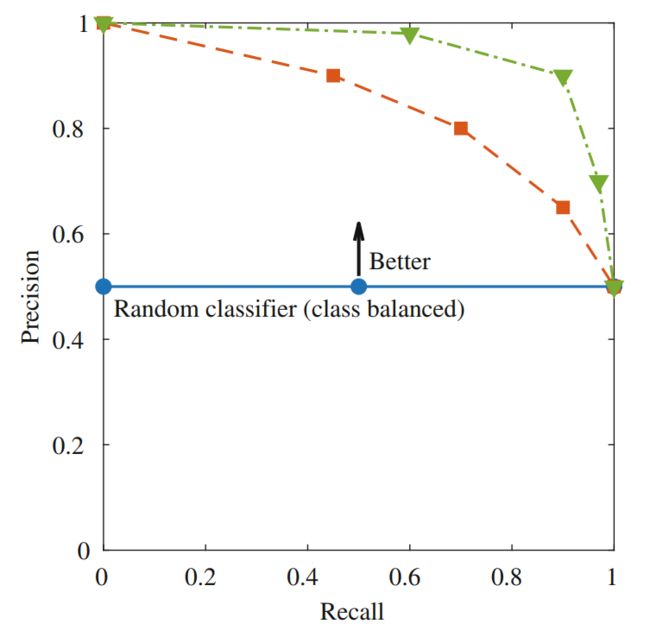
精度-召回率(PR)曲线是另一种与ROC曲线类似的方法。PR曲线使用阈值化之前的分类器输出。PR曲线绘制了不同阈值下灵敏度和精度之间的权衡(如图5所示)。对于随机分类器，PR曲线是在

处的一条水平线，其中P和N分别是阳性类和阴性类的总数。性能优于随机的分类器的PR曲线高于随机分类器的PR曲线。例如，类平衡数据集的随机分类器在0.5处是一条水平线(如图5中的蓝线所示)，而优于随机分类器的PR曲线高于0.5(如图5中的红绿线所示)。有人认为当数据集高度倾斜(即类不平衡)时，PR曲线可以更好地评估分类器的性能。PR曲线下面积(AUC-PR)提供了可用作性能指标的单一度量。

图5.三种假设分类器的PR曲线。当数据是类平衡时，蓝线对应于随机分类器。绿曲线对应的分类器性能优于红曲线对应的分类器。

应用

大量的研究集中在基于EEG的机器学习上。基于EEG的机器学习有许多应用。一个重要的应用是使用机器学习从EEG中识别和提取神经系统疾病的生物标志物，例如阿尔茨海默症，帕金森，癫痫和癫痫发作，以及痴呆。机器学习在EEG中的其他应用包括脑机接口(BCI)、睡眠分期、睡意检测、以及微睡眠检测和预测等。尽管应用不同，但机器学习过程在这些EEG系统的实现遵循类似的步骤。接下来，本文将进一步详细介绍机器学习在EEG中的两个应用，即BCI与微睡眠检测和预测。

①脑机接口(BCI)

BCI系统使用户能够通过大脑活动与周围环境进行交互。BCI系统对重度残疾患者尤为重要，BCI系统使他们能够在不使用任何肌肉或周围神经的情况下控制假肢或环境。这些系统通常使用EEG来记录大脑的电活动，因为EEG成本低，时间分辨率高，相关风险低。

一类BCI系统专注于运动图像。在这种范式中，参与者在心理上模拟执行一系列动作。BCI系统的目的是利用大脑活动来区分不同类型的运动。一些研究调查了运动想象BCI，并取得了相对可接受的表现。使用类似的概念，目前已经开发了其他系统来控制机械臂和无人机。在这些系统中，采用了多种特征提取方法，包括CSP，小波变换系数，频谱特征，卷积神经网络和自编码器。此外，一系列分类器已用于分离运动图像任务，例如LDA，SVM，kNN，集成分类器，朴素贝叶斯和深度神经网络。

P300拼写器是BCI的另一种范式。在P300拼写器中，参与者会看到一个字母表，其中一行或一列的强度随机增加。要求参与者将注意力集中在兴趣字母上，该字母会随机突出显示。这种强度的变化会在参与者的大脑活动中产生反应，该反应发生在字母突出显示后大约300ms，即P300。使用P300模式，BCI系统可以识别感兴趣的字母。P300拼写器范式已在文献中得到了广泛研究，并取得了相对较好的表现。已有几种分类器被用于在P300拼写范式中识别感兴趣的字母，例如LDA、SVM、深度神经网络、集成分类器和随机森林。

还有其他BCI范式，例如稳态视觉诱发电位(SSVEP)、听觉诱发电位、视觉诱发电位和混合诱发电位。这些范式也是许多研究的主题。有许多研究对不同的BCI范式进行了调查，并且发表的数量正在增加。这些研究结果表明，改善严重神经和肌肉骨骼疾病患者的生活质量具有广阔的前景。

②微睡眠的实时检测与预测

微睡眠是指一种短暂的(＜15s)无意识发作，是一种与睡眠相关的意识丧失。微睡眠是在没有任何征兆的情况下发生的，通常伴随着一些行为线索，如点头、眼睛下垂和闭眼缓慢。大多数人在读书或听课时都有过微睡眠的经历。但是，如果微睡眠发生在驾驶等某些特定任务中，可能会导致严重后果。此外，许多正常休息的健康个体在执行一项长时间的单调任务时，会频繁地经历微睡眠。因此，微睡眠的检测和预测对于需要长时间不受影响的视觉运动表现的职业(如驾驶)来说是至关重要的。

一些研究调查了从EEG信号中检测微睡眠。在这些研究中，参与者执行了一个连续的跟踪任务来模拟驾驶任务。然后从跟踪表现和面部视频定义微睡眠。对于微睡眠的每种状态，利用相应的EEG窗口来提取特征。利用这些特征，然后应用各种机器学习算法来检测微睡眠。

对微睡眠的预测也是许多研究的主题。在这些研究中，与微睡眠状态相对应的EEG窗口的选择是通过使EEG窗口先于相应的微睡眠状态一定时间的方式进行的。在性能方面，微睡眠检测和预测系统已经实现了相对较高的AUC-ROC值(例如，0.95)。然而，这些系统的精度相对较低。微睡眠系统存在的挑战之一是，微睡眠数据具有固有的高类别不平衡。此外，类别失衡比例因人而异。这为训练系统和评估其性能带来了复杂性。

结论

大量的研究集中在EEG及其在医学、神经科学、康复和其他领域的应用。EEG和机器学习领域的整合为开发基于EEG的精确预测系统提供了一个框架。本文概述了基于EEG系统的机器学习算法。将该过程分为EEG数据采集，预处理，特征提取，特征降维，分类和性能评估。对于每个步骤，都进行了介绍并讨论了潜在的挑战。此外，机器学习将在基于EEG的系统及其应用中发挥越来越重要的作用。特别是，深度神经网络将成为开发基于EEG的系统越来越受欢迎的选择。

参考文献（上下滑动查看）：

1. Tong, S.,Thakor, N.V.: Quantitative EEG analysis methods and clinical applications. Artech House engineering in medicine & biology series. Artech House (2009)

2. Lopes da Silva, F.: EEG and MEG: Relevance to neuroscience. Neuron 80(5), 1112–1128 (2013). https://doi.org/10.1016/j.neuron.2013.10.017

3. Logothetis, N.K.: What we can do and what we cannot do with fMRI. Nature 453, 869 (2008). https://doi.org/10.1038/nature06976

4. Irani, F., Platek, S.M., Bunce, S., Ruocco, A.C., Chute, D.: Functional near infrared spectroscopy (fNIRS): An emerging neuroimaging technology with important applications for the study of brain disorders. Clin. Neuropsychol. 21(1), 9-37 (2007). https://doi.org/10.1080/13854040600910018

5. Buzsaki, G.: Rhythms of the brain. Oxford University Press, New York (2006)

6. Cohen, M.X.: Analyzing neural time series data: Theory and practice. The MIT Press, Cambridge (2014)

7. Widmann, A., Schröger, E., Maess, B.: Digital filter design for electrophysiological data - A practical approach. J. Neurosci. Meth. 250, 34–46 (2015). https://doi.org/10.1016/j.jneumeth.2014.08.002

8. Mullen, T.R., Kothe, C.A.E., Chi, Y.M., Ojeda, A., Kerth, T., Makeig, S., Jung, T.-P., Cauwenberghs, G.: Real-time neuroimaging and cognitive monitoring using wearable dry EEG. IEEE Trans. Biomed. Eng. 62(11), 2553-2567 (2015). https://doi.org/10.1109/TBME.2015.2481482

9. Delorme, A., Sejnowski, T., Makeig, S.: Enhanced detection of artifacts in EEG data using higher-order statistics and independent component analysis. NeuroImage 34(4), 1443–1449 (2007). https://doi.org/10.1016/j.neuroimage.2006.11.004

10. Cohen, M.X.: Comparison of linear spatial filters for identifying oscillatory activity in multichannel data. J. Neurosci. Meth. 278, 1-12 (2017). https://doi.org/10.1016/j.jneumeth.2016.12.016

11. Jonmohamadi, Y., Poudel, G., Innes, C., Weiss, D., Krueger, R., Jones, R.: Comparison of beamformers for EEG source signal reconstruction. Biomed. Signal Process. Control 14(Supplement C), 175-188 (2014). https://doi.org/10.1016/j.bspc.2014.07.014

12. Clercq, W.D., Vergult, A., Vanrumste, B., Van Paesschen, W., Van Huffel, S.: Canonical correlation analysis applied to remove muscle artifacts from the electroencephalogram. IEEE Trans. Biomed. Eng. 53(12), 2583-2587 (2006). https://doi.org/10.1109/TBME.2006.879459

13. Nolan, H., Whelan, R., Reilly, R.B.: FASTER: Fully automated statistical thresholding for EEG artifact rejection. J. Neurosci. Meth. 192(1), 152-162 (2010). https://doi.org/10.1016/j.jneumeth.2010.07.015

14. Hastie, T., Tibshirani, R., Friedman, J.: The Elements of Statistical Learning: Data Mining, Inference, and Prediction. Springer Series in Statistics, 2nd edn. Springer, New York (2009)

15. Murphy, K.P.: Machine Learning: A Probabilistic Perspective. MIT Press, Cambridge (2013)

16. Bishop, C.M.: Pattern Recognition and Machine Learning. Springer, Berlin/Heidelberg (2006)

17. Müller, K.-R., Tangermann, M., Dornhege, G., Krauledat, M., Curio, G., Blankertz, B.: Machine learning for real-time single-trial EEG-analysis: From brain–computer interfacing to mental state monitoring. J. Neurosci. Meth. 167(1), 82-90 (2008). https://doi.org/10.1016/j.jneumeth.2007.09.022

18. Lemm, S., Schafer, C., Curio, G.: BCI competition 2003-data set III: Probabilistic modeling of sensorimotor mu; rhythms for classification of imaginary hand movements. IEEE Trans. Biomed. Eng. 51(6), 1077-1080 (2004). https://doi.org/10.1109/TBME.2004.827076

19. Dauwan, M., Linszen, M.M.J., Lemstra, A.W., Scheltens, P., Stam, C.J., Sommer, I.E.: EEGbased neurophysiological indicators of hallucinations in Alzheimer’s disease: Comparison with dementia with Lewy bodies. Neurobiol. Aging 67, 75-83 (2018). https://doi.org/10.1016/j.neurobiolaging.2018.03.013

20. Kumar, Y., Dewal, M.L., Anand, R.S.: Epileptic seizure detection using DWT based fuzzy approximate entropy and support vector machine. Neurocomputing 133, 271-279 (2014). https://doi.org/10.1016/j.neucom.2013.11.009

21. Buriro, A.B., Shoorangiz, R., Weddell, S.J., Jones, R.D.: Predicting microsleep states using EEG inter-channel relationships. IEEE Trans. Neural Syst. Rehabilitat. Eng. 26(12), 2260-2269 (2018). https://doi.org/10.1109/TNSRE.2018.2878587

22. Davidson, P.R., Jones, R.D., Peiris, M.T.R.: EEG-based lapse detection with high temporal resolution. IEEE Trans. Biomed. Eng. 54(5), 832-839 (2007). https://doi.org/10.1109/TBME.2007.893452

23. Shahidi Zandi, A., Tafreshi, R., Javidan, M., Dumont, G.A.: Predicting epileptic seizures in scalp EEG based on a variational Bayesian Gaussian mixture model of zero-crossing intervals. EEE Trans. Biomed. Eng. 60(5), 1401-1413 (2013). https://doi.org/10.1109/TBME.2012.2237399

24. Kwon, Y.-H., Shin, S.-B., Kim, S.-D.: Electroencephalography based fusion two-dimensional(2D)-convolution neural networks (CNN) model for emotion recognition system. Sensors 18(5), 1383 (2018). https://doi.org/10.3390/s18051383

25. Sen, B., Peker, M., Çavu¸ soglu, A., Çelebi, F.: A comparative study on classification of sleep stage based on EEG signals using feature selection and classification algorithms. J. Med. Syst. 38(3), 1-21 (2014). https://doi.org/10.1007/s10916-014-0018-0

26. Hjorth, B.: EEG analysis based on time domain properties. Electroencephalography Clin. Neurophysiol. 29(3), 306-310 (1970). https://doi.org/10.1016/0013-4694(70)90143-4

27. Vidaurre, C., Krämer, N., Blankertz, B., Schlögl, A.: Time domain parameters as a feature for EEG-based brain-computer interfaces. Neural Netw. 22(9), 1313–1319 (2009). https://doi.org/10.1016/j.neunet.2009.07.020

28. Chapotot, F., Becq, G.: Automated sleep–wake staging combining robust feature extraction, artificial neural network classification, and flexible decision rules. Int. J. Adap. Control Signal Process. 24(5), 409-423 (2010). https://doi.org/10.1002/acs.1147

29. Padilla-Buritica, J.I., Martinez-Vargas, J.D., Castellanos-Dominguez, G.: Emotion discrimination using spatially compact regions of interest extracted from imaging EEG activity. Front. Comput. Neurosci. 10, 55 (2016). https://doi.org/10.3389/fncom.2016.00055

30. Cecchin, T., Ranta, R., Koessler, L., Caspary, O., Vespignani, H., Maillard, L.: Seizure lateralization in scalp EEG using Hjorth parameters. Clin. Neurophysiol. 121(3), 290–300(2010). https://doi.org/10.1016/j.clinph.2009.10.033

31. Greene, B.R., Faul, S., Marnane, W.P., Lightbody, G., Korotchikova, I., Boylan, G.B.: A comparison of quantitative EEG features for neonatal seizure detection. Clin. Neurophysiol. 119(6), 1248-1261 (2008). https://doi.org/10.1016/j.clinph.2008.02.001

32. Imtiaz, S.A., Saremi-Yarahmadi, S., Rodriguez-Villegas, E.: Automatic detection of sleep spindles using Teager energy and spectral edge frequency. In: Proceedings of IEEE Biomedical Circuits System Conference, pp. 262-265. IEEE (2013). https://doi.org/10.1109/BioCAS.2013.6679689

33. Di Ieva, A., Grizzi, F., Jelinek, H., Pellionisz, A.J., Losa, G.A.: Fractals in the neurosciences, Part I: General principles and basic neurosciences. The Neuroscientist 20(4), 403-417 (2014). https://doi.org/10.1177/1073858413513927

34. Hosseini, S.A.: A computational framework to discriminate different anesthesia states from EEG signal. Biomed. Eng. Appl. Basis Commun. 30(03), 1850020 (2018). https://doi.org/10.4015/S1016237218500205

35. Pavithra, M., NiranjanaKrupa, B., Sasidharan, A., Kutty, B.M., Lakkannavar, M.: Fractal dimension for drowsiness detection in brainwaves. In: Proc. Int. Conf. Contemp. Comput. Informat. (IEEE, 2014) pp. 757-761. https://doi.org/10.1109/IC3I.2014.7019676

36. Yan, R., Zhang, C., Spruyt, K., Wei, L., Wang, Z., Tian, L., Li, X., Ristaniemi, T., Zhang, J., Cong, F.: Multi-modality of polysomnography signals’ fusion for automatic sleep scoring. Biomed. Signal Process. Control 49, 14-23 (2019). https://doi.org/10.1016/j.bspc.2018.10.001

37. Paramanathan, P., Uthayakumar, R.: Application of fractal theory in analysis of human electroencephalographic signals. Comput. Biol. Med. 38(3), 372-378 (2008). https://doi.org/10.1016/j.compbiomed.2007.12.004

38. Polychronaki, G.E., Ktonas, P.Y., Gatzonis, S., Siatouni, A., Asvestas, P.A., Tsekou, H., Sakas, D., Nikita, K.S.: Comparison of fractal dimension estimation algorithms for epileptic seizure onset detection. J. Neural Eng. 7(4), 046007 (2010)

39. Ahmadlou, M., Adeli, H., Adeli, A.: Fractality and a wavelet-chaos-methodology for EEGbased diagnosis of Alzheimer disease. Alzheimer Dis. Assoc. Disorders 25(1) (2011)

40. Sabeti, M., Katebi, S.D., Boostani, R., Price, G.W.: A new approach for EEG signal

classification of schizophrenic and control participants. Expert Syst. Appl. 38(3), 2063–2071(2011). https://doi.org/10.1016/j.eswa.2010.07.145

41. D’Alessandro, M., Vachtsevanos, G., Hinson, A., Esteller, R., Echauz, J., Litt, B.: A genetic approach to selecting the optimal feature for epileptic seizure prediction. In: Proceedings of International Conference IEEE Engineering Medical Biology Society, Vol. 23, pp. 1703-1706. IEEE (2001). https://doi.org/10.1109/IEMBS.2001.1020544

42. Blythe, D., Haufe, A.J.S., Müller, K.-R., Nikulin, V.V.: The effect of linear mixing in the EEG on Hurst exponent estimation. NeuroImage 99, 377–387 (2014). https://doi.org/10.1016/j.neuroimage.2014.05.041

43. Carreras, B.A., van Milligen, B.P., Pedrosa, M.A., Balbín, R., Hidalgo, C., Newman, D.E., Sánchez, E., Frances, M., García-Cortés, I., Bleuel, J., Endler, M., Riccardi, C., Davies, S., Matthews, G.F., Martines, E., Antoni, V., Latten, A., Klinger, T.: Self-similarity of the plasma edge fluctuations. Phys. Plasmas 5(10), 3632–3643 (1998). https://doi.org/10.1063/1.873081

44. Yuan, Q., Zhou, W., Li, S., Cai, D.: Epileptic EEG classification based on extreme learning machine and nonlinear features. Epilepsy Res. 96(1–2), 29–38 (2011) . https://doi.org/10.1016/j.eplepsyres.2011.04.013

45. Wang, X.-W., Nie, D., Lu, B.-L.: Emotional state classification from EEG data using machine learning approach. Neurocomputing 129, 94–106 (2014). https://doi.org/10.1016/j.neucom.2013.06.046

46. Oppenheim, A.V., Willsky, A.S., Nawab, S.H.: Signals & Systems. Prentice-Hall, Inc., Upper Saddle River (1996)

47. Kaplan, A.Y., Fingelkurts, A.A., Fingelkurts, A.A., Borisov, S.V., Darkhovsky, B.S.: Nonstationary nature of the brain activity as revealed by EEG/MEG: Methodological, practical and conceptual challenges. Signal Process. 85(11), 2190-2212 (2005) . https://doi.org/10.1016/j.sigpro.2005.07.010

48. Muthuswamy, J., Thakor, N.V.: Spectral analysis methods for neurological signals. J. Neurosci. Meth. 83(1), 1-14 (1998). https://doi.org/10.1016/S0165-0270(98)00065-X

49. Gross, J.: Analytical methods and experimental approaches for electrophysiological studies of brain oscillations. J. Neurosci. Meth. 228, 57–66 (2014). https://doi.org/10.1016/j.jneumeth.2014.03.007

50. Mallat, S.: A wavelet tour of signal processing, 3rd edn (pp. 795–805). Academic Press, Boston (2009)

51. Freeman, W.J.: Hilbert transform for brain waves. Scholarpedia 2(1), 1338 (2007). https://doi.org/10.4249/scholarpedia.1338

52. Mallat, S.G., Zhang, Z.: Matching pursuits with time-frequency dictionaries. IEEE Trans. Signal Process. 41(12), 3397–3415 (1993) . https://doi.org/10.1109/78.258082

53. Durka, P.J., Blinowska, K.J.: Analysis of EEG transients by means of matching pursuit. Ann. Biomed. Eng. 23(5), 608–611 (1995) . https://doi.org/10.1007/BF02584459

54. Welch, P.: The use of fast Fourier transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms. IEEE Trans. Audio Electroacous. 15(2), 70–73 (1967). https://doi.org/10.1109/TAU.1967.1161901

55. Babiloni, C., Pistoia, F., Sarà, M., Vecchio, F., Buffo, P., Conson, M., Onorati, P., Albertini, G., Rossini, P.M.: Resting state eyes-closed cortical rhythms in patients with locked-in-syndrome: An EEG study. Clin. Neurophysiol. 121(11), 1816-1824 (2010) . https://doi.org/10.1016/j.clinph.2010.04.027

56. Shoorangiz, R., Weddell, S.J., Jones, R.D.: Bayesian multi-subject factor analysis to predict microsleeps from EEG power spectral features. In: Proceedings of International Conference of the IEEE Engineering in Medicine and Biology Society, Vol. 39, pp. 4183–4186. IEEE(2017) . https://doi.org/10.1109/EMBC.2017.8037778

57. Lin, F., Ko, L., Chuang, C., Su, T., Lin, C.: Generalized EEG-based drowsiness prediction system by using a self-organizing neural fuzzy system. IEEE Trans. Circuits Syst. I Regular Papers 59(9), 2044–2055. (2012) https://doi.org/10.1109/TCSI.2012.2185290

58. Sabeti, M., Katebi, S., Boostani, R.: Entropy and complexity measures for EEG signal classification of schizophrenic and control participants. Artif. Intell. Med. 47(3), 263–274(2009). https://doi.org/10.1016/j.artmed.2009.03.003

59. Kannathal, N., Choo, M.L., Acharya, U.R., Sadasivan, P.K.: Entropies for detection of epilepsy in EEG. Comput. Meth. Prog. Biomed. 80(3), 187–194 (2005). https://doi.org/10.1016/j.cmpb.2005.06.012

60. Chen, L.-l., Zhao, Y., Zhang, J., Zou, J.-Z.: Automatic detection of alertness/drowsiness from physiological signals using wavelet-based nonlinear features and machine learning. Expert Syst. Appl. 42(21), 7344–7355 (2015). https://doi.org/10.1016/j.eswa.2015.05.028

61. Yeo, M.V.M., Li, X., Shen, K., Wilder-Smith, E.P.V.: Can SVM be used for automatic EEG detection of drowsiness during car driving? Safety Sci. 47(1), 115–124 (2009). https://doi.org/10.1016/j.ssci.2008.01.007

62. Ramoser, H., Muller-Gerking, J., Pfurtscheller, G.: Optimal spatial filtering of single trial EEG during imagined hand movement. IEEE Trans. Rehabilitat. Eng. 8(4), 441–446 (2000). https://doi.org/10.1109/86.895946

63. Blankertz, B., Tomioka, R., Lemm, S., Kawanabe, M., Muller, K.-R.: Optimizing spatial filters for robust EEG single-trial analysis. IEEE Signal Process. Mag. 25(1), 41–56 (2008). https://doi.org/10.1109/MSP.2008.4408441

64. Ang, K.K., Chin, Z.Y., Zhang, H., Guan, C.: Filter bank common spatial pattern (FBCSP) in brain-computer interface. In: Proceedings of International Joint Conference on Neural Network, pp. 2390–2397. IEEE, (2008). https://doi.org/10.1109/IJCNN.2008.4634130

65. Ang, K.K., Chin, Z.Y., Wang, C., Guan, C., Zhang, H.: Filter bank common spatial pattern algorithm on BCI competition IV datasets 2a and 2b. Front. Neurosci. 6, 39 (2012). https://doi.org/10.3389/fnins.2012.00039

66. Lotte, F., Guan, C.: Regularizing common spatial patterns to improve BCI designs: Unified theory and new algorithms. IEEE Trans. Biomed. Eng. 58(2), 355–362 (2011). https://doi.org/10.1109/TBME.2010.2082539

67. Kang, H., Choi, S.: Bayesian common spatial patterns for multi-subject EEG classification. Neural Netw. 57(Supplement C), 39–50 (2014). https://doi.org/10.1016/j.neunet.2014.05.012

68. Wu, W., Chen, Z., Gao, X., Li, Y., Brown, E.N., Gao, S.: Probabilistic common spatial patterns for multichannel EEG analysis. IEEE Trans. Pattern Anal. Mach. Intell. 37(3), 639-653 (2015). https://doi.org/10.1109/TPAMI.2014.2330598

69. Ang, K.K., Chin, Z.Y., Zhang, H., Guan, C.: Mutual information-based selection of optimal spatial–temporal patterns for single-trial EEG-based BCIs. Pattern Recogn. 45(6), 2137–2144(2012). https://doi.org/10.1016/j.patcog.2011.04.018

70. Mwangi, B., Tian, T.S., Soares, J.C.: A review of feature reduction techniques in neuroimaging. Neuroinformatics 12(2), 229–244 (2014). https://doi.org/10.1007/s12021-013-9204-3

71. Chandrashekar, G., Sahin, F.: A survey on feature selection methods. Comput. Electr. Eng. 40(1), 16–28 (2014) . https://doi.org/10.1016/j.compeleceng.2013.11.024

72. Cai, J., Luo, J., Wang, S., Yang, S.: Feature selection in machine learning: A new perspective. Neurocomputing 300, 70–79 (2018). https://doi.org/10.1016/j.neucom.2017.11.077

73. Miao, J., Niu, L.: A survey on feature selection. Proc. Comput. Sci. 91, 919–926 (2016). https://doi.org/10.1016/j.procs.2016.07.111

74. Mitra, P., Murthy, C.A., Pal, S.K.: Unsupervised feature selection using feature similarity. IEEE Trans. Pattern Anal. Mach. Intell. 24(3), 301–312 (2002). https://doi.org/10.1109/34.990133

75. Lee, J.A., Verleysen, M.: Nonlinear Dimensionality Reduction, 1st edn. Springer Publishing Company, Incorporated (2007)

76. Singh, D.A.A.G., Balamurugan, S.A.A., Leavline, E.J.: An unsupervised feature selection algorithm with feature ranking for maximizing performance of the classifiers. Int. J. Automat. Comput. 12(5), 511–517 (2015) . https://doi.org/10.1007/s11633-014-0859-5

77. Subasi, A., Gursoy, M.I.: EEG signal classification using PCA, ICA, LDA and support vector machines. Expert Syst. Appl. 37(12), 8659–8666 (2010). https://doi.org/10.1016/j.eswa.2010.06.065

78. ai Li, M., Yong Luo, X., fu Yang, J.: Extracting the nonlinear features of motor imagery EEG using parametric t-SNE. Neurocomputing 218, 371–381 (2016). https://doi.org/10.1016/j.neucom.2016.08.083

79. Birjandtalab, J., Pouyan, M.B., Cogan, D., Nourani, M., Harvey, J.: Automated seizure detection using limited-channel EEG and non-linear dimension reduction. Comput. Biol. Med. 82, 49–58 (2017). https://doi.org/10.1016/j.compbiomed.2017.01.011

80. Yu, X., Chum, P., Sim, K.-B.: Analysis the effect of PCA for feature reduction in nonstationary EEG based motor imagery of BCI system. Optik 125(3), 1498–1502 (2014). https://doi.org/10.1016/j.ijleo.2013.09.013

81. Schölkopf, B., Smola, A., Müller, K.-R.: Nonlinear component analysis as a kernel eigenvalue problem. Neural Comput. 10(5), 1299–1319 (1998)

82. Tipping, M.E., Bishop, C.M.: Probabilistic principal component analysis. J. R. Stat. Soc. Ser. B (Statistical Methodology) 61(3), 611–622 (1999). https://doi.org/10.1111/1467-9868.00196

83. Bishop, C.M.: Variational principal components. In: Proceedings of International Conference on Artificial Neural Networks, Vol. 9, pp. 509–514. Institution of Engineering and Technology(1999). https://doi.org/10.1049/cp_19991160

84. Ding, X., He, L., Carin, L.: Bayesian robust principal component analysis. IEEE Trans. Image Process. 20(12), 3419–3430 (2011). https://doi.org/10.1109/TIP.2011.2156801

85. Guyon, I.: An introduction to variable and feature selection. J. Mach. Learn. Res. 3, 1157–1182 (2003)

86. Kwak, N., Choi, C.-H.: Input feature selection by mutual information based on Parzen window. IEEE Trans. Pattern Anal. Mach. Intell. 24(12), 1667–1671 (2002). https://doi.org/10.1109/TPAMI.2002.1114861

87. Battiti, R.: Using mutual information for selecting features in supervised neural net learning. IEEE Trans. Neural Netw. 5(4), 537–550 (1994). https://doi.org/10.1109/72.298224

88. Arvaneh, M., Guan, C., Ang, K., Quek, C.: Mutual information-based optimization of sparse spatio-spectral filters in brain-computer interface. Neural Comput. Appl. 25(3–4), 625–634(2014). https://doi.org/10.1007/s00521-013-1523-7

89. Yang, J., Zhang, L., Xu, Y., Yang, J.-Y.: Beyond sparsity: the role of L1-optimizer in pattern classification. Pattern Recogn. 45(3), 1104–1118 (2012). https://doi.org/10.1016/j.patcog.2011.08.022

90. Tibshirani, R.: Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B(Methodological) 58(1), 267–288 (1996)

91. Liu, M., Zhang, D., Shen, D.: Ensemble sparse classification of Alzheimer’s disease. NeuroImage 60(2), 1106–1116 (2012). https://doi.org/10.1016/j.neuroimage.2012.01.055

92. Fell, J., Röschke, J., Mann, K., Schäffner, C.: Discrimination of sleep stages: A comparison between spectral and nonlinear EEG measures. Electroencephalography Clin. Neurophysiol. 98(5), 401–410 (1996). https://doi.org/10.1016/0013-4694(96)95636-9

93. Lin, Y., Wang, C., Jung, T., Wu, T., Jeng, S., Duann, J., Chen, J.: EEG-based emotion recognition in music listening. IEEE Trans. Biomed. Eng. 57(7), 1798–1806 (2010). https://doi.org/10.1109/TBME.2010.2048568

94. Schlögl, A., Lee, F., Bischof, H., Pfurtscheller, G.: Characterization of four-class motor imagery EEG data for the BCI-competition 2005. J. Neural Eng. 2(4), L14–L22 (2005). https://doi.org/10.1088/1741-2560/2/4/l02

95. Quitadamo, L.R., Cavrini, F., Sbernini, L., Riillo, F., Bianchi, L., Seri, S., Saggio, G.: Support vector machines to detect physiological patterns for EEG and EMG-based human–computer interaction: A review. J. Neural Eng. 14(1), 011001 (2017)

96. Hearst, M.A., Dumais, S.T., Osuna, E., Platt, J., Scholkopf, B.: Support vector machines. IEEE Intell. Syst. Appl. 13(4), 18–28 (1998). https://doi.org/10.1109/5254.708428

97. Schölkopf, B.: The kernel trick for distances. In: Leen, T.K., Dietterich, T.G., Tresp, V. (eds.) Advances in Neural Information Processing Systems, pp. 301–307. MIT Press (2001)

98. Roth, V., Steinhage, V.: Nonlinear discriminant analysis using kernel functions. In: Solla, S.A., Leen, T.K., Müller, K. (eds.) Advances in Neural Information Processing Systems, pp. 568–574. MIT Press (2000)

99. Nicolaou, N., Georgiou, J.: Detection of epileptic electroencephalogram based on permutation entropy and support vector machines. Expert Syst. Appl. 39(1), 202–209 (2012). https://doi.org/10.1016/j.eswa.2011.07.008

100. Tito, M., Cabrerizo, M., Ayala, M., Jayakar, P., Adjouadi, M.: A comparative study of intracranial EEG files using nonlinear classification methods. Ann. Biomed. Eng. 38(1), 187–99 (2010)

101. Lawrence, N.D., Schölkopf, B.: Estimating a kernel Fisher discriminant in the presence of label noise. In: Proceedings of International Conference on Machine Learning, ICML’01, Vol. 18, pp. 306–313. ACM (2001)

102. Kayikcioglu, T., Aydemir, O.: A polynomial fitting and k-NN based approach for improving classification of motor imagery BCI data. Pattern Recogn. Lett. 31(11), 1207–1215 (2010). https://doi.org/10.1016/j.patrec.2010.04.009

103. Safavian, S.R., Landgrebe, D.: A survey of decision tree classifier methodology. IEEE Trans. Syst. Man Cybern. 21(3), 660–674 (1991). https://doi.org/10.1109/21.97458

104. Polat, K., Güne¸ s, S.: Classification of epileptiform EEG using a hybrid system based on decision tree classifier and fast Fourier transform. Appl. Math. Comput. 187(2), 1017–1026(2007). https://doi.org/10.1016/j.amc.2006.09.022

小伙伴们点星标关注茗创科技，将第一时间收到精彩内容推送哦～