排序一 冒泡排序
冒泡排序(Bubble Sort)
- 重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。
- 算法的名字由来是因为越大的元素会经由交换慢慢“浮”到数列的顶端,故名。 —百度百科
- 时间复杂度:最好 O(n)=O(n);平均O(n)=O(n²);最差O(n)=O(n²)
- 空间复杂度:O(n)=O(1)
- 稳定性: 稳定
算法描述
- 比较相邻的元素。如果第一个比第二个大,就交换他们两个。
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大的数。
- 针对所有的元素重复以上的步骤,除了最后一个。
- 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。—百度百科
排序示例
数组S: [9,1,5,3,8,7]
第一趟:[1,5,3,8,7,9]
第二趟:[1,3,5,7,8,9]
第三趟:[1,3,5,7,8,9]
第三趟无元素交换,排序完成。
示例代码
pulic static void BubbleSort(int[] S){ //C#
bool isSwapped = true;
for (int i = S.Length - 1; i >= 1 && isSwapped; i--){
isSwapped = false;
for (int j = 0; j < i; j++){
if (S[j] > S[j + 1]){
S.Swap(j, j + 1);
isSwapped = true;
}
}
}
}def bubble_sort(s): #Python
swapped = True
i = len(s) - 1
while i > 0 and swapped:
swapped = False
for j in range(0, i):
if s[j] > s[j+1]:
s[j], s[j+1] = s[j+1], s[j]
swapped = True
i -= 1地精排序(Gnome Sort)
- 类冒泡排序,先朝一个方向冒泡,一旦发生交换就往回冒泡。
- 时间复杂度:最好 O(n)=O(n);平均O(n)=O(n²);最差O(n)=O(n²)
- 空间复杂度:O(n)=O(1)
- 稳定性: 稳定
算法描述
The algorithm always finds the first place where two adjacent elements are in the wrong order, and swaps them. It takes advantage of the fact that performing a swap can introduce a new out-of-order adjacent pair only next to the two swapped elements. It does not assume that elements forward of the current position are sorted, so it only needs to check the position directly previous to the swapped elements. — Wiki
- 从左至右比较相邻的元素。
若两元素无序,交换它们,执行2。
若已找到最右端,则结束 - 从该交换位置往回冒泡(即从右往左比较)。
若回冒途中遇到两个元素无序,则交换,继续回冒。
若回冒途中遇到两个元素有序,则停止回冒,从新执行1。
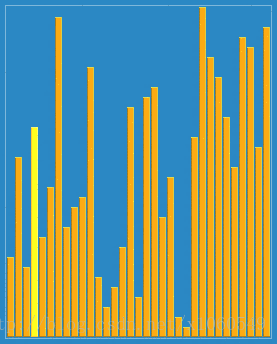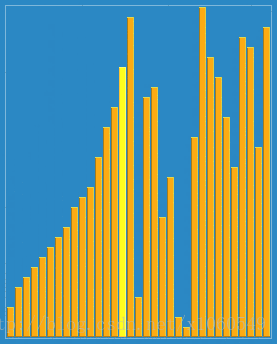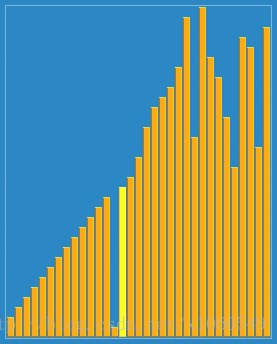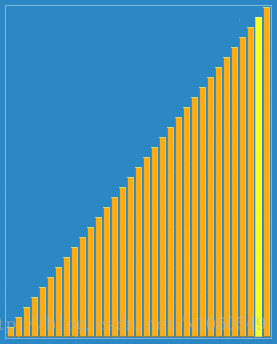
图片来自维基百科
排序示例
数组S: [9,1,5,3,8,7]
第一趟:[1,9,5,3,8,7]
第二趟:[1,5,9,3,8,7]
第三趟:[1,5,3,9,8,7]
回冒: [1,3,5,9,8,7]
第四趟:[1,3,5,8,9,7]
第五趟:[1,3,5,8,7,9]
回冒: [1,3,5,7,8,9]
第六趟:[1,3,5,7,8,9]
已到最右端,排序完成
示例代码
public static void GnomeSort1(int[] S){ //C#
int i = 0;
while (i < S.Length){
if (i == 0 || S[i] >= S[i-1]){
i++;
} else{
S.Swap(i, i-1);
i--;
}
}
}
public static void GnomeSort2(int[] S){
for (int i = 1; i < S.Length; i++){
for (int j = i; j > 0 && S[j-1] > S[j]; j--){
S.Swap(j, j-1);
}
}
}def gnome_sort1(s): #Python
i = 0
while i < len(s):
if i == 0 or s[i] >= s[i-1]:
i += 1
else:
s[i-1], s[i] = s[i], s[i-1]
i -= i
def gnome_sort2(s):
for i in range(1,len(s)):
for j in range(i, 0, -1):
if s[j-1] <= s[j]:
break
s[j-1], s[j] = s[j], s[j-1]
鸡尾酒排序(Cocktail Sort)
- 类冒泡排序,双向循环。
- 时间复杂度:最好 O(n)=O(n);平均O(n)=O(n²);最差O(n)=O(n²)
- 空间复杂度:O(n)=O(1)
- 稳定性: 稳定
算法描述
- 从最低位到最高位冒泡,将最大元素上浮
- 从最高位到最低位冒泡,将最小元素下层
- 若1和2过程中无交换,则排序结束。
- 最低位加一,最高位减一。最低位小于等于最高位,则执行1。否则排序结束。
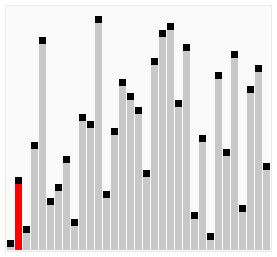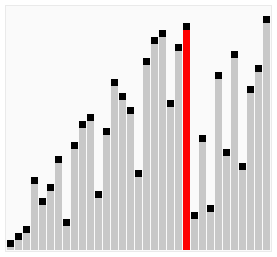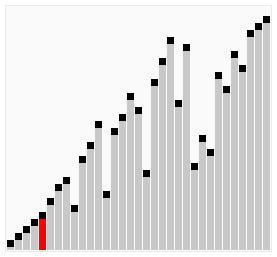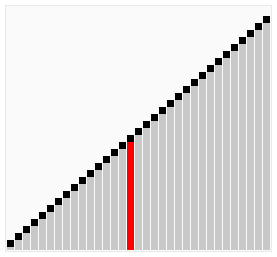
图片来自维基百科
排序示例
数组S: [9,1,5,3,8,7]
第一趟往高位冒泡:[1,5,3,8,7,9]
第一趟往低位冒泡:[1,3,5,7,8,9]
第二趟往高位冒泡:[1,3,5,7,8,9]
无交换排序结束。
示例代码
public static void CocktailSort(int[] S){ //C#
bool isSwapped = true;
int begin = 0;
int end = S.Length - 1;
while (isSwapped && begin <= end){
isSwapped = false;
for (int i = begin; i < end; i++){//低位到高位冒泡
if (S[i] > S[i + 1]){
S.Swap(i, i + 1);
isSwapped = true;
}
}
end--;
if (!isSwapped){
break;
}
isSwapped = false;
for (int i = end; i >= begin; i--){//高位到低位冒泡
if (S[i] > S[i + 1]){
S.Swap(i, i + 1);
isSwapped = true;
}
}
begin++;
}
}def cocktail_sort(s): #Python
swapped = True
begin = 0
end = len(s) - 1
while swapped and begin <= end:
swapped = False
for i in range(begin, end):
if s[i] > s[i+1]:
s[i], s[i+1] = s[i+1], s[i]
swapped = True
if not swapped:
break
end -= 1
swapped = False
for i in range(end, begin-1, -1):
if s[i] > s[i+1]:
s[i], s[i+1] = s[i+1], s[i]
swapped = True
begin += 1奇偶排序(OddEven Sort)
- 类冒泡排序,重复两趟分别对奇数位和偶数位进行冒泡排序。
- 时间复杂度:最好 O(n)=O(n);平均O(n)=O(n²);最差O(n)=O(n²)
- 空间复杂度:O(n)=O(1)
- 稳定性: 不稳定
算法描述
奇偶排序法的思路是在数组中重复两趟扫描。第一趟扫描选择所有的数据项对,a[j]和a[j+1],j是奇数(j=1, 3, 5……)。如果它们的关键字的值次序颠倒,就交换它们。第二趟扫描对所有的偶数数据项进行同样的操作(j=2, 4,6……)。重复进行这样两趟的排序直到数组全部有序。 —百度百科
排序示例
数组S: [9,1,5,3,8,7]
第一趟:[1,9,3,5,7,8]
第二趟:[1,3,5,9,7,8]
第三趟:[1,3,5,7,8,9]
第四趟:[1,3,5,7,8,9]
无交换排序结束。
示例代码
public static void OddEvenSort(int[] S){ //C#
bool isSwapped = true;
while (isSwapped){
isSwapped = false;
for (int i = 1; i < S.Length - 1; i += 2){ //奇数位冒泡排序
if (S[i] > S[i + 1]){
S.Swap(i, i + 1);
isSwapped = true;
}
}
for (int i = 0; i < S.Length - 1; i += 2){ //偶数位冒泡排序
if (S[i] > S[i + 1]){
S.Swap(i, i + 1);
isSwapped = true;
}
}
}
}def oddevent_sort(s): #Python
swapped = True
while swapped:
swapped = False
for i in range(1, len(s)-1, 2):
if s[i] > s[i+1]:
s[i], s[i+1] = s[i+1], s[i]
swapped = True
for i in range(0, len(s)-1, 2):
if s[i] > s[i+1]:
s[i], s[i+1] = s[i+1], s[i]
swapped = True梳排序(Comb Sort)
- 改良自泡沫排序和快速排序,以一个递减的间距进行冒泡排序。
- 时间复杂度:最好 O(n)=O(nlogn);平均O(n)=O(n²/2^p);最差O(n)=O(n²)
- 空间复杂度:O(n)=O(1)
- 稳定性: 不稳定
算法描述
在泡沫排序中,只比较阵列中相邻的二项,即比较的二项的间距(Gap)是1,梳排序提出此间距其实可大于1,改自插入排序的希尔排序同样提出相同观点。梳排序中,开始时的间距设定为阵列长度,并在循环中以固定比率递减,通常递减率设定为1.3。在一次循环中,梳排序如同泡沫排序一样把阵列从首到尾扫描一次,比较及交换两项,不同的是两项的间距不固定于1。如果间距递减至1,梳排序假定输入阵列大致排序好,并以泡沫排序作最后检查及修正。 —百度百科
排序示例
数组S: [9,1,5,3,8,7]
第一趟:[8,1,5,3,9,7]–gap=4
第二趟:[3,1,5,8,9,7]–gap=3
第三趟:[3,1,5,7,9,8]–gap=2
第四趟:[1,3,5,7,8,9]–gap=1
无交换排序结束。
示例代码
public static void CombSort(int[] S){ //C#
int gap = S.Length; //比较间距
const shrink = 1.3f;//递减率
while (gap > 1){
gap = (int)Math.Floor(gap / shrink);
gap = gap > 1 ? gap : 1;
for (int i = 0; i + gap < S.Length; i++){
if (S[i] > S[i + gap]){
S.Swap(i, i+ gap);
}
}
}
}def comb_sort(s): #Python
gap = len(s)
SHRINK = 1.3
while gap > 1:
gap = int(gap / SHRINK)
if gap < 1:
gap = 1
for i in range(0, len(s) - gap):
if s[i] > s[i+gap]:
s[i], s[i+gap] = s[i+gap], s[i]注: 前文C#中数组元素交换是用扩展的方式定义的:
public static class Utility{
public static void Swap(this T[] S, int x, int y){
T temp = S[x];
S[x] = S[y];
S[y] = temp;
}
} 文中若有什么错误,欢迎留言指正。
转载请保留出处:http://blog.csdn.net/x1060549/article/details/78689258