前向传播、反向传播、更新梯度
1. 从误差传递的角度以动图演示前、反向传播
①前向传播计算误差
②反向传播传递误差
③前向传播更新梯度
2.从梯度传递的角度以计算演示前、反向传播
①前向传播计算误差
首先根据输入 [ x 1 , x 2 ] \left [ x1,x2 \right ] [x1,x2]和 [ w 1 , w 2 , . . . , w 6 ] \left [ w1,w2,...,w6 \right ] [w1,w2,...,w6],计算隐藏层 [ h 1 , h 2 , h 3 ] \left [ h1,h2,h3 \right ] [h1,h2,h3]的输出结果
h 1 = x 1 ∗ w 1 + x 2 ∗ w 2 + b 1 h1=x1\ast w1+x2\ast w2+b1 h1=x1∗w1+x2∗w2+b1
h 1 = 0.05 × 0.15 + 0.10 × 0.20 + 0.45 = 0.4775 h1=0.05\times 0.15+0.10\times 0.20+0.45=0.4775 h1=0.05×0.15+0.10×0.20+0.45=0.4775
f 1 ( h 1 ) = 1 1 + e − h 1 = 1 1 + e − 0.4775 ≈ 0.61715736 f_{1}\left ( h1 \right )=\frac{1}{1+e^{-h1}}=\frac{1}{1+e^{-0.4775}}\approx 0.61715736 f1(h1)=1+e−h11=1+e−0.47751≈0.61715736
f 1 ( h 2 ) = 1 1 + e − h 2 = 1 1 + e − 0.4925 ≈ 0.62069519 f_{1}\left ( h2 \right )=\frac{1}{1+e^{-h2}}=\frac{1}{1+e^{-0.4925}}\approx 0.62069519 f1(h2)=1+e−h21=1+e−0.49251≈0.62069519
f 1 ( h 3 ) = 1 1 + e − h 3 = 1 1 + e − 0.5075 ≈ 0.62422023 f_{1}\left ( h3 \right )=\frac{1}{1+e^{-h3}}=\frac{1}{1+e^{-0.5075}}\approx 0.62422023 f1(h3)=1+e−h31=1+e−0.50751≈0.62422023
其次根据隐藏层输出 [ f 1 ( h 1 ) , f 1 ( h 2 ) , f 1 ( h 3 ) ] \left [ f_{1}\left ( h1 \right ),f_{1}\left ( h2 \right ) ,f_{1}\left ( h3 \right )\right ] [f1(h1),f1(h2),f1(h3)]和 [ w 7 , w 8 , . . . , w 12 ] \left [ w7,w8,...,w12 \right ] [w7,w8,...,w12],计算输出层 [ o 1 , o 2 ] \left [ o1,o2 \right ] [o1,o2]的输出结果
o 1 = f 1 ( h 1 ) ∗ w 7 + f 1 ( h 2 ) ∗ w 8 + f 1 ( h 3 ) ∗ w 9 + b 2 o1=f_{1}\left ( h1 \right )\ast w7+f_{1}\left ( h2 \right )\ast w8+f_{1}\left ( h3 \right )\ast w9+b2 o1=f1(h1)∗w7+f1(h2)∗w8+f1(h3)∗w9+b2
h 1 = 0.61715736 × 0.50 + 0.62069519 × 0.55 + 0.62422023 × 0.60 + 0 ≈ 1.02449317 h1=0.61715736\times 0.50+0.62069519\times 0.55+0.62422023\times 0.60 +0\approx 1.02449317 h1=0.61715736×0.50+0.62069519×0.55+0.62422023×0.60+0≈1.02449317
f 2 ( o 1 ) = 1 1 + e − o 1 = 1 1 + e − 1.02449317 ≈ 0.73584689 f_{2}\left ( o1 \right )=\frac{1}{1+e^{-o1}}=\frac{1}{1+e^{-1.02449317}}\approx 0.73584689 f2(o1)=1+e−o11=1+e−1.024493171≈0.73584689
f 2 ( o 2 ) = 1 1 + e − o 2 = 1 1 + e − 1.30380409 ≈ 0.78647451 f_{2}\left ( o2 \right )=\frac{1}{1+e^{-o2}}=\frac{1}{1+e^{-1.30380409}}\approx 0.78647451 f2(o2)=1+e−o21=1+e−1.303804091≈0.78647451
最后根据真实数据 [ O 1 , O 2 ] \left [ O1,O2 \right ] [O1,O2]和输出层输出结果 [ f 2 ( o 1 ) , f 2 ( o 2 ) ] \left [ f_{2}\left ( o1 \right ),f_{2}\left ( o2 \right ) \right ] [f2(o1),f2(o2)],计算总体误差
E = 1 2 [ O 1 − f 2 ( o 1 ) ] 2 + 1 2 [ O 2 − f 2 ( o 2 ) ] 2 E=\frac{1}{2}\left [ O1-f_{2}\left ( o1 \right ) \right ]^{2}+\frac{1}{2}\left [ O2-f_{2}\left ( o2 \right ) \right ]^{2} E=21[O1−f2(o1)]2+21[O2−f2(o2)]2
E ≈ 0.5 × ( 0.01 − 0.73584689 ) 2 + 0.5 × ( 0.99 − 0.78647451 ) 2 ≈ 0.28413817 E\approx 0.5\times \left ( 0.01-0.73584689 \right )^{2}+0.5\times \left ( 0.99-0.78647451 \right )^{2}\approx0.28413817 E≈0.5×(0.01−0.73584689)2+0.5×(0.99−0.78647451)2≈0.28413817
至此,前向传播过程结束
②反向传播计算梯度
首先我们从整个网络中把o1节点连接的几个权重都摘出来,先计算w7的梯度
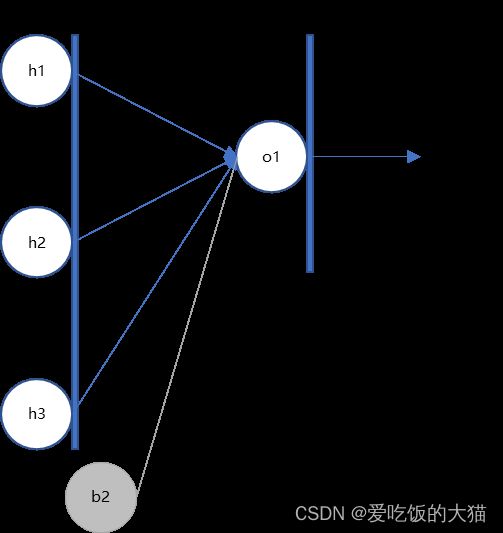
然后我们再从上图中抽象出计算w7的梯度的链式法则:

首先,我们可以列出如下的链式求导法则,计算误差E对w7的梯度:
∂ E ∂ w 7 = ∂ ( E 1 + E 2 ) ∂ w 7 = ∂ E 1 ∂ w 7 = ∂ E 1 ∂ f 2 ( o 1 ) ∗ ∂ f 2 ( o 1 ) ∂ o 1 ∗ ∂ o 1 ∂ w 7 \frac{\partial E}{\partial w7}=\frac{\partial \left ( E_{1}+E_{2} \right )}{\partial w7}=\frac{\partial E_{1}}{\partial w7}=\frac{\partial E_{1}}{\partial f_{2}\left ( o1 \right )}\ast \frac{\partial f_{2}\left ( o1 \right )}{\partial o1}\ast\frac{\partial o1}{\partial w7} ∂w7∂E=∂w7∂(E1+E2)=∂w7∂E1=∂f2(o1)∂E1∗∂o1∂f2(o1)∗∂w7∂o1
然后针对其中三个因子,逐个计算其结果:
-
E 1 = 1 2 [ O 1 − f 2 ( o 1 ) ] 2 E_{1}=\frac{1}{2}\left [ O1-f_{2}\left ( o1 \right ) \right ]^{2} E1=21[O1−f2(o1)]2
∂ E 1 ∂ f 2 ( o 1 ) = 2 × 1 2 [ O 1 − f 2 ( o 1 ) ] × ( − 1 ) ≈ 2 × 1 2 × ( 0.01 − 0.73584689 ) × ( − 1 ) ≈ 0.72584689 \frac{\partial E_{1}}{\partial f_{2}\left ( o1 \right )}=2\times \frac{1}{2}\left [ O1-f_{2}\left ( o1 \right ) \right ]\times \left ( -1 \right )\approx 2\times \frac{1}{2}\times \left ( 0.01-0.73584689 \right )\times \left ( -1 \right )\approx 0.72584689 ∂f2(o1)∂E1=2×21[O1−f2(o1)]×(−1)≈2×21×(0.01−0.73584689)×(−1)≈0.72584689 -
f 2 ( o 1 ) = 1 1 + e − o 1 f_{2}\left ( o1 \right )=\frac{1}{1+e^{-o1}} f2(o1)=1+e−o11
f 2 ( o 1 ) ∂ o 1 = e − o 1 ( 1 + e − o 1 ) 2 = f 2 ( o 1 ) [ 1 − f 2 ( o 1 ) ] ≈ 0.73584689 × ( 1 − 0.73584689 ) ≈ 0.19437624 \frac{f_{2}\left ( o1 \right )}{\partial o1}=\frac{e^{-o1}}{\left ( 1+e^{-o1} \right )^{2}}=f_{2}\left ( o1 \right )\left [ 1-f_{2}\left ( o1 \right ) \right ]\approx 0.73584689\times \left ( 1-0.73584689 \right )\approx 0.19437624 ∂o1f2(o1)=(1+e−o1)2e−o1=f2(o1)[1−f2(o1)]≈0.73584689×(1−0.73584689)≈0.19437624
- o 1 = f 1 ( h 1 ) ∗ w 7 + b 2 o1=f_{1}\left ( h1 \right )\ast w7+b2 o1=f1(h1)∗w7+b2
∂ o 1 ∂ w 7 = f 1 ( h 1 ) ≈ 0.61715736 \frac{\partial o1}{\partial w7}=f_{1}\left ( h1 \right )\approx 0.61715736 ∂w7∂o1=f1(h1)≈0.61715736
- total
∂ E ∂ w 7 = 0.72584689 × 0.19437624 × 0.61715736 ≈ 0.08707312 \frac{\partial E}{\partial w7}=0.72584689\times 0.19437624\times 0.61715736\approx 0.08707312 ∂w7∂E=0.72584689×0.19437624×0.61715736≈0.08707312
至此,我们便算出了w7的梯度,同理我们也可以算出剩余权重的梯度。
类似于w7的链式法则,这里同样帮助各位列出w1对应的链式法则:

计算过程便不列出来了,方式也一样,只不过是多了一条分支,计算出的各个梯度如下:
| ∂ E ∂ w 1 ≈ 0.00056889 \frac{\partial E}{\partial w1}\approx 0.00056889 ∂w1∂E≈0.00056889 | ∂ E ∂ w 2 ≈ 0.00113779 \frac{\partial E}{\partial w2}\approx 0.00113779 ∂w2∂E≈0.00113779 | ∂ E ∂ w 3 ≈ 0.00063182 \frac{\partial E}{\partial w3}\approx 0.00063182 ∂w3∂E≈0.00063182 | ∂ E ∂ w 4 ≈ 0.00126364 \frac{\partial E}{\partial w4}\approx 0.00126364 ∂w4∂E≈0.00126364 |
| ∂ E ∂ w 5 ≈ 0.00069474 \frac{\partial E}{\partial w5}\approx 0.00069474 ∂w5∂E≈0.00069474 | ∂ E ∂ w 6 ≈ 0.00138949 \frac{\partial E}{\partial w6}\approx 0.00138949 ∂w6∂E≈0.00138949 | ∂ E ∂ w 7 ≈ 0.08707312 \frac{\partial E}{\partial w7}\approx 0.08707312 ∂w7∂E≈0.08707312 | ∂ E ∂ w 8 ≈ 0.08757226 \frac{\partial E}{\partial w8}\approx 0.08757226 ∂w8∂E≈0.08757226 |
| ∂ E ∂ w 9 ≈ 0.08806960 \frac{\partial E}{\partial w9}\approx 0.08806960 ∂w9∂E≈0.08806960 | ∂ E ∂ w 10 ≈ 0.02109352 \frac{\partial E}{\partial w10}\approx 0.02109352 ∂w10∂E≈0.02109352 | ∂ E ∂ w 11 ≈ 0.02121444 \frac{\partial E}{\partial w11}\approx 0.02121444 ∂w11∂E≈0.02121444 | ∂ E ∂ w 12 ≈ 0.02133492 \frac{\partial E}{\partial w12}\approx 0.02133492 ∂w12∂E≈0.02133492 |
至此,所有权重对应的梯度计算完毕,接下来可以进行更新权重和偏置了
③前向传播更新权重和偏置
采用的权重更新公式为
w + = w − η ∂ E ∂ w , η = 0.5 w^{+}=w-\eta \frac{\partial E}{\partial w},\eta=0.5 w+=w−η∂w∂E,η=0.5
| w 1 + = w 1 − η ∂ E ∂ w 1 ≈ 0.14971556 w1^{+}=w1-\eta \frac{\partial E}{\partial w1}\approx0.14971556 w1+=w1−η∂w1∂E≈0.14971556 | w 2 + = w 2 − η ∂ E ∂ w 2 ≈ 0.19943111 w2^{+}=w2-\eta \frac{\partial E}{\partial w2}\approx0.19943111 w2+=w2−η∂w2∂E≈0.19943111 |
| w 3 + = w 3 − η ∂ E ∂ w 3 ≈ 0.24968409 w3^{+}=w3-\eta \frac{\partial E}{\partial w3}\approx0.24968409 w3+=w3−η∂w3∂E≈0.24968409 | w 4 + = w 4 − η ∂ E ∂ w 4 ≈ 0.29936818 w4^{+}=w4-\eta \frac{\partial E}{\partial w4}\approx0.29936818 w4+=w4−η∂w4∂E≈0.29936818 |
| w 5 + = w 5 − η ∂ E ∂ w 5 ≈ 0.36965263 w5^{+}=w5-\eta \frac{\partial E}{\partial w5}\approx0.36965263 w5+=w5−η∂w5∂E≈0.36965263 | w 6 + = w 6 − η ∂ E ∂ w 6 ≈ 0.39930523 w6^{+}=w6-\eta \frac{\partial E}{\partial w6}\approx0.39930523 w6+=w6−η∂w6∂E≈0.39930523 |
| w 7 + = w 7 − η ∂ E ∂ w 7 ≈ 0.45646344 w7^{+}=w7-\eta \frac{\partial E}{\partial w7}\approx0.45646344 w7+=w7−η∂w7∂E≈0.45646344 | w 8 + = w 8 − η ∂ E ∂ w 8 ≈ 0.50621387 w8^{+}=w8-\eta \frac{\partial E}{\partial w8}\approx0.50621387 w8+=w8−η∂w8∂E≈0.50621387 |
| w 9 + = w 9 − η ∂ E ∂ w 9 ≈ 0.55596520 w9^{+}=w9-\eta \frac{\partial E}{\partial w9}\approx0.55596520 w9+=w9−η∂w9∂E≈0.55596520 | w 1 0 + = w 10 − η ∂ E ∂ w 10 ≈ 0.63945324 w10^{+}=w10-\eta \frac{\partial E}{\partial w10}\approx0.63945324 w10+=w10−η∂w10∂E≈0.63945324 |
| w 1 1 + = w 11 − η ∂ E ∂ w 11 ≈ 0.68939278 w11^{+}=w11-\eta \frac{\partial E}{\partial w11}\approx0.68939278 w11+=w11−η∂w11∂E≈0.68939278 | w 1 2 + = w 12 − η ∂ E ∂ w 12 ≈ 0.73933254 w12^{+}=w12-\eta \frac{\partial E}{\partial w12}\approx0.73933254 w12+=w12−η∂w12∂E≈0.73933254 |
采用的偏置更新公式为
b + = b − η ∂ E ∂ b , μ = 0.5 b^{+}=b-\eta \frac{\partial E}{\partial b},\mu=0.5 b+=b−η∂b∂E,μ=0.5
这里就不放LaTeX公式了,这个太长一大串了,偷个懒放个图片



