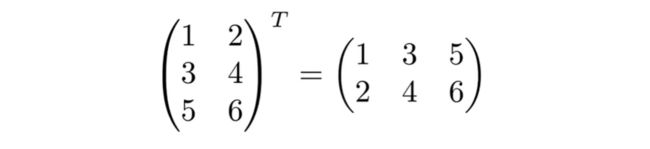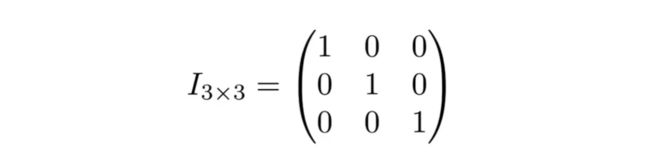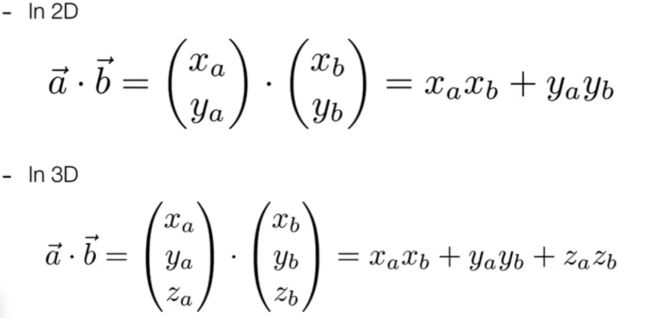计算机图形学入门

---

前言

计算机图形学入门，通过学习视频和查询资料，记录以便之后查询回顾。

一、二维和三维的仿射变化

通过向量和点坐标与矩阵的乘积，完成二维和三维视图中数据的变化。首先需要回顾下最基础的知识：

• 矩阵乘积的条件：M✖N • N✖P=M✖P(前者的列数得和后者的行数对应上)
  

• 矩阵不满足乘积的交换律（先旋转再平移和先平移再旋转是不同的，后面会有论证）

• 转置矩阵：行列互换后的矩阵

• 单位矩阵（对角为1，其他为0的方阵）

• 两方阵（N✖N阶）的乘积为单位矩阵，则两矩阵互为逆矩阵

• 二维三维的旋转拉伸线性操作都可以通过和对应矩阵相乘的方式获得

• 点乘可以用来区别前后
  
  那么ab向量的乘积如何计算呢？
  

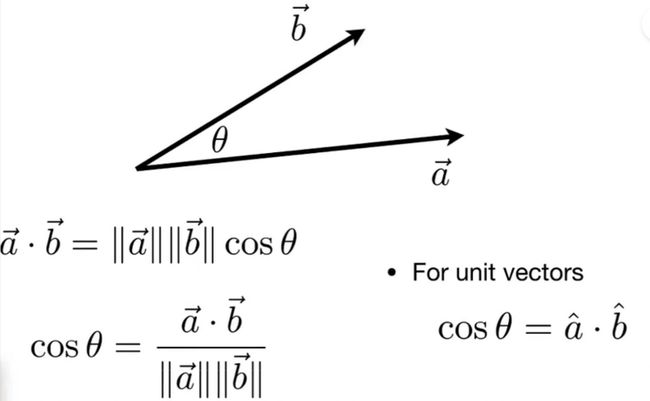
• 叉乘可以用区别左右和里外（使用右手螺旋坐标系辅助）
  
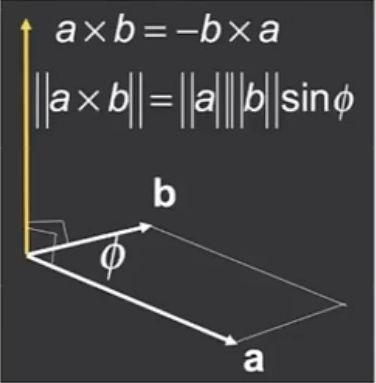
  叉乘的结果还是一个向量，结果大小上等于ab长度和sinθ的乘积，方向符合右手螺旋定则。
  在坐标系下叉乘的结果如下：
  
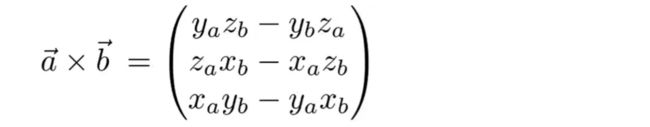
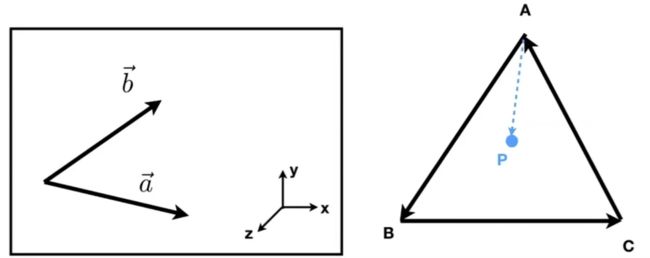
  a向量叉乘b向量，得到的向量的z数值为正数，说明在左侧。
  利用这条特性，可以判断某个点是不是在三角形内部。
  

二维

使用矩阵表示简单变换

不额外说明的情况下，旋转的圆心是坐标轴原点；旋转的方向是逆时针旋转。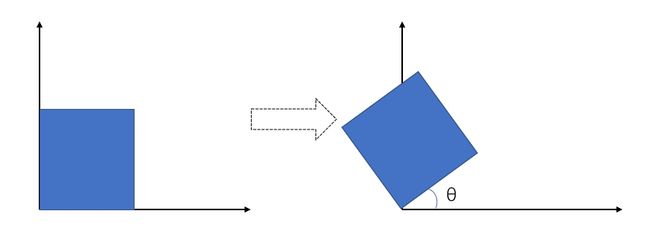

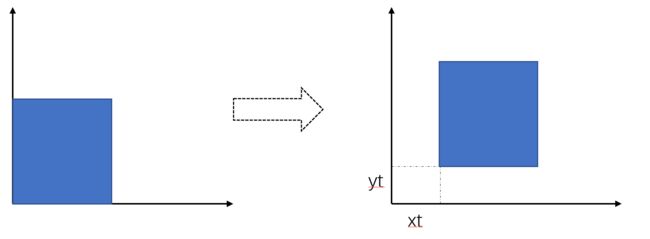
观察这些变化都可以写成与矩阵相乘的形式

观察顺时针和逆时针旋转θ角度的矩阵，可以发现它两刚好为彼此的转置。且乘积正好是单位矩阵E，所以称为正交矩阵。（这点在view transformation的时候会用到）
一个新的问题，其他的变化都可以用和矩阵相乘的形式表达，但是平移不可以，有没有什么办法可以统一一下?

齐次坐标系

为了解决刚刚说到的问题，将线性变化在数学上进行统一表达，使用比N维度多一维的方阵来表示N维度的线性变化。

考虑到向量平移变化前后和位置无关，应该保持一致。规定向量的齐次表示最后一位为0。齐次坐标系下的点如果最后一位不为0，则需要归一化处理。

为什么还要归一化呢？明明齐次坐标系的点带入的时候都是1，线性变化最后一行又只有最后一位是1，那么w怎么会是非1的呢？一开始我也有疑惑，其实是因为目前我们只认识了线性变化，所有的线性变化最后一行都是固定为0 0 0 …0 1的格式。但实际有的变化前几位非0的。这做个伏笔，遇到再说。

到了这里，通过齐次坐标系就完美地将平移也能通过矩阵乘积的形式表现了。
那么如何用齐次坐标系表示先旋转θ角度，再平移这件事呢？

不难发现，平移和旋转影响地范围是相对固定的，而且我可以用一个矩阵表示两个（以上）矩阵的乘积，是不是也就是说可以用一个矩阵表示更多的复合变化了？！
另外我们再看个图说明下矩阵为什么不能交换着乘。

记得：先应用地矩阵书写时候最靠近向量/点矩阵。

三维

使用矩阵表示三维空间中经典变换

了解了二维的齐次坐标系，三维其实不用害怕，和二维基本一致。

其他的都和二维的逻辑保持一致，但是观察三维绕y轴旋转的旋转矩阵和其他的旋转略有不同，和二维绕原点顺时针旋转θ角度很像，sinθ在右上角，-sinθ在左下角。可明明旋转的角度是逆时针啊？
这里涉及一个问题，xyz轴彼此之间叉乘的结果，xy右手螺旋能得到z，yz也能得到x。但是，xz却得到的是-y，朝下的。如图，俯视看如右上角图，仰视如右下角图。原本逆时针的变化变化成了顺时针，所以矩阵的表示变成了顺时针变化。

其实一个三维物体按照任意轴的旋转，该任意轴可能是不经过原点的，该怎么做？
首先将该轴平移到过原点，绕旋转轴旋转就可以分解成xyz轴方向上旋转结果的组合，旋转之后再平移回最初的点。

罗德里格斯方程，表示了三维空间的旋转，在这里我参考了些资料，做了一个推导的总结，感兴趣可以看看如何用矩阵形式表示罗德里格斯公式。

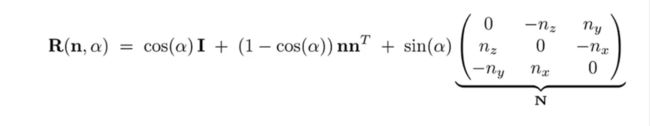
**什么是万向节死锁？**旋转过程中谈及的万向节死锁，简单地说绕着xyz轴依次旋转任意角度，如果中间绕y旋转是±90°，那么旋转前的z轴和旋转后的z轴重合了。也就是说“浪费了一个维度的表示”，换句话说，我只要y配合另一个轴这两个轴的旋转就可以表示这种绕三个轴的旋转结果。

二、三维向二维的变化

三维向二维的转换，需要经过M（model transformation）V（view transformation） P（projection transformation），对应日常中人物模型摆好pose，相机找到方位视角，最后按下快门形成照片。

具体分类如下：
观测变化viewing transformations

• 视图变化 camera/view transformation
• 投影变化projection transformation
  - 正交投影 Orthographic projection
  - 透视投影 perspective projection

视图变化 camera/view transformation

因为相机和被拍摄物体的相对位置（包括角度方位）相同的时候，投影出来的照片都是一致的。

为了之后好计算，引入相机坐标系。所以不妨始终想方设法将相机移到相机坐标系原点。
同时规定相机镜头朝向定为g向量，相机头顶正上方为t向量。
（红色标注为世界坐标系，白色标注为相机坐标系）

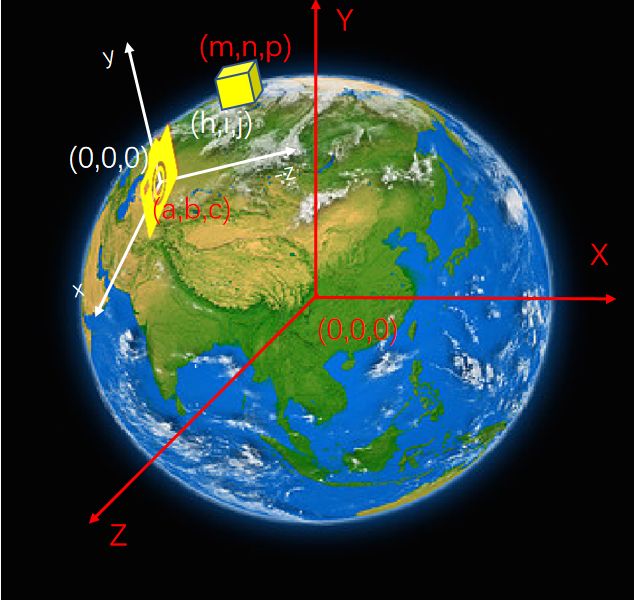
将相机的坐标移到原点后，使其头顶t向量和相机坐标系Y轴重合，g轴和相机坐标系-Z轴重合。
其实更好理解的意思就是新建一个坐标系（相机坐标系），以相机所在位置作为坐标原点，相机的头顶方向当成相机坐标系y轴，观测的正前方当成-z轴。但是，世界坐标系下的相机真实坐标要经过怎样的**“变化”才能写成相机坐标系呢？（实际相机根本没移动**，只是作为了世界坐标系和相机坐标系转换的桥梁，可以理解成一种映射，换句话说，世界坐标系下相机的位置和体态通过怎么样的矩阵能映射成我们规定的相机坐标系呢？）

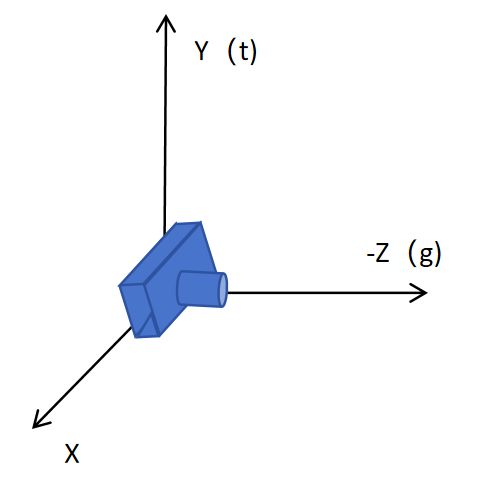
照相机在三维空间的位置可以是任意的，那么如何将它从任意的位置转换为原点，还得要求其通过旋转，使得t和Y轴重合，g和-Z轴重合（又因为在原点，所以gxt肯定和X轴重合）。

平移到原点的矩阵很好写，相机坐标的世界坐标系是(xe,ye,ze,1)，那么它平移到原点的矩阵如下：

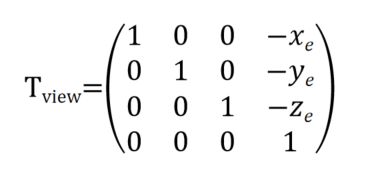
可要将g旋转至-Z，t旋转至Y，gxt旋转至X，写起来就难多了。怎么解决呢？因为二维中我们知道旋转和恢复（顺逆时针）互为正交矩阵，彼此为转置的关系，能不能先想反过来的事：从X转至gxt（也就是从（1,0,0,0）变成一个齐次坐标系下表示的gxt向量（Xgxt，Ygxt，Zgxt，0）），从Y轴转置t（也就是（0,1,0,0）变成t向量（Xt,Yt,Zt,0）），从-Z轴转至g（也就是从（0,0,0,-1）变成g向量（Xg,Yg,Zg,0））。

以上R-1view矩阵就是我们要的逆矩阵（按照说的代入即可，-Z轴的变化看着别扭，代入后系数-1提前就是g向量）。
根据旋转矩阵的特性，那么他的逆变化的矩阵就是它对应的转置，也就是我们要求的矩阵。大功告成~（这一步我理解了好久。。。）

相机经过这样的变化后，为了保证相对位置不变（相机都变位置了，为了拍的照片一样，模型也得跟着变啊）所有的被拍摄物体也需要经过这样的变化。这也就是为什么称为camera/view transformation 视图变化。

投影变化 projection transformation

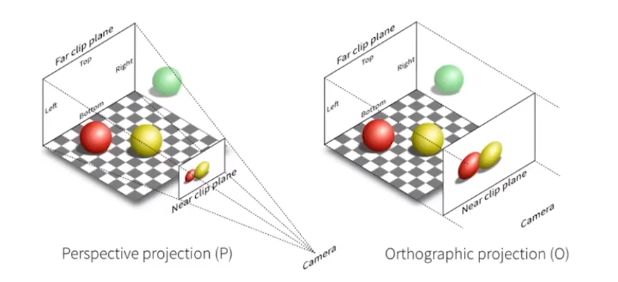
正交投影 Orthographic projection

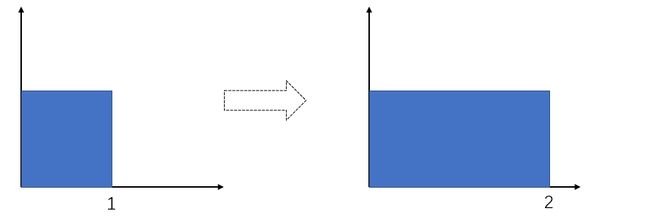
忽略物体在人眼/相机中近大远小的规律，也就是投影过程中直接忽略Z轴数值。
将其压缩到X在[-1,1]，Y在[-1,1]的正方形框中。
先将物体正则化（canonical cube ，X在[-1,1]，Y在[-1,1],Z在[-1,1]的立方体）

透视投影 perspective projection

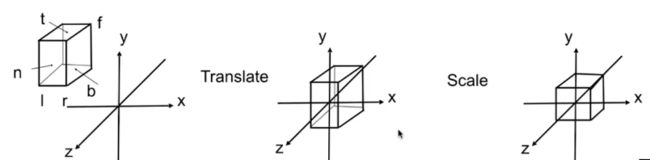
透视投影符合人眼/相机近大远小的规律，通过规定一个近端n平面，和远端f平面：近端平面内所有点xyz均不变；远端点所有点的z不变，但xy经过压缩成和近端n平面一样大小范围；介于近端和远端之间的平面，xy也需要缩小为n平面大小，同时z也可能会有相应的变化，之后会验证。如下图：

这么做的目的其实就是为了在一个屏幕的大小下，能用n平面的大小表示从n->f在内的所有平面，除n以外，所有的平面都需要经过特定的压缩（一个从透视转变为矩形的变换），这个变化的切面可以用以下图形表示：

那么这个矩阵要怎么求呢？根据相似三角形能得到压缩前后x’，y’的表达形式。那么任何一个点经过透视投影的矩阵变化后，都可以写成（nx,ny,暂定,z）的形式。

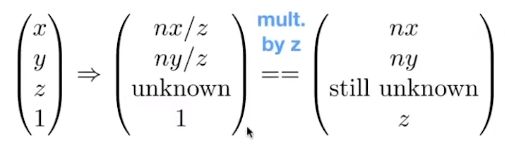
由以上公式可以推出该矩阵其中三行

那么投影矩阵的第三行怎么求呢？回想下一开始规定的n平面和f平面我们还有些特性没有使用：通过在n平面任意一个点，z都为n的特点，带入

由于未知一行前两位和xy有关，但输出结果和xy均无关，所以前两位必须为0。

可得等式：

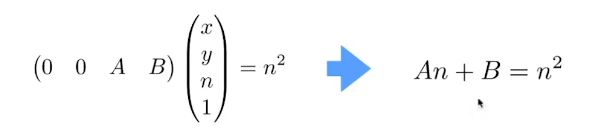
再利用投影过f平面中心的点，其z轴数值不变，所以齐次坐标下表示为（0,0,f,1），同样可经过前面推出的投影矩阵变化为（0,0,f平方,1）

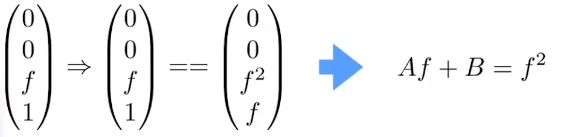
由两个等式可推算出A和B，透视投影向正交变化的矩阵：

引发一个新的问题：在（f,n）区间内任何一点的z数值经过透视投影变化后，是靠近近端还是远端了？（可以拿中点(n+f)/2来计算)，结果是远离n平面了。
完整推导可参考GANSES101透视投影的理解

经过persp->ortho变化后，整个视野从一个梯形体变为一个长方体，为了后期正视投影，还需要将长方体正则化，同样经过正则变换变为一个[-1,1]的立方体中。完整公式如下：

至此，正交投影和透视投影前视域的处理已经完毕，如果细心就会发现，经过正则变化后，图形在xy轴上还是经过了一定压缩或拉伸变化的，已经无法表示实际的图形比例了，之后还需要怎么处理呢？

另外，透视投影过程中为什么远平面z设置为不变？为什么近平面远平面中所有的z不都设置为不变？查了很久没看到非常准确官方得解答，这里简单得汇总描述了下，不一定完全准确，但应该是那么个道理，大家可以批判地看。

三、光栅化

视口变化及像素充填

目的就是将三维的图形经过进一步变化，转换到屏幕上，这一步我们称为视口变化（视觉窗口变化）。
之前的变化把视锥中所有不同深度的平面统一和近平面n一样大。但n平面具体有多大呢？
根据视锥，相机过中轴垂直于n平面上下边构成的角度，称为垂直可视角度。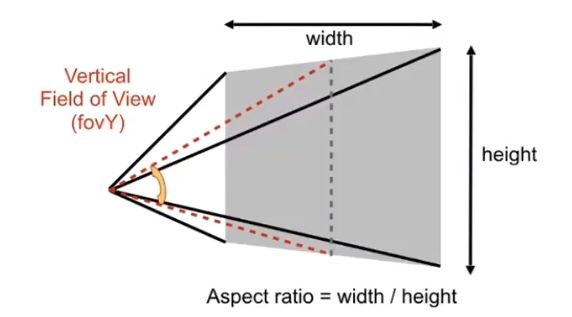
已知可视角度Y，那么可以求得t，两倍的t也就是height，再根据宽高比，可以知道width。

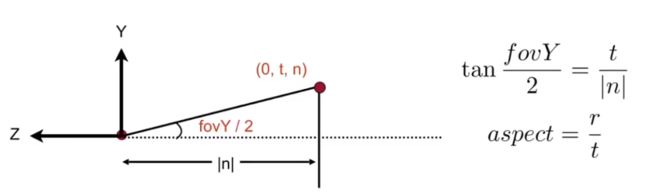
然后我们从屏幕左下角开始，为每一个像素的左下角点做标记。那么所有的像素则从（0,0）变为（width-1，height-1）。像素的中心则表示为（x+0.5，y+0.5），每个像素的宽高为1。

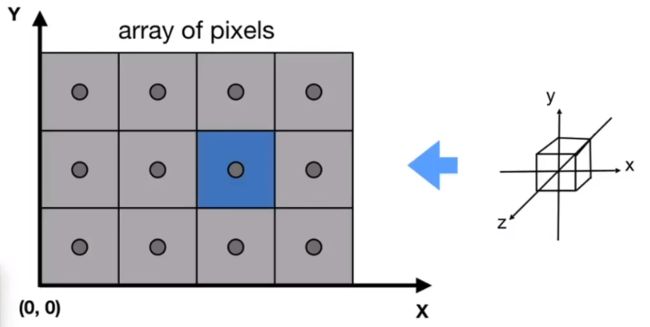
所以我们现在要做的是把正则变化后x内[-1,1]和y[-1,1]转换到[0,width]x[0,height]，其中z轴方向先不做变化，矩阵变化中对应3行3列的1。对应的视口变化矩阵如下：

经过MVP变化和视口变化之后，就可以将一个三维空间的点表示成屏幕上的点，上一节中我们还有个问题：经过正则变化后，图形的比例已经发生变化了，经过视口变化为什么又能变化回来呢？让我们用正交投影为例，代入计算下：

光栅化最重要的一点：对屏幕内一系列点的中心是否满足函数条件（判断像素点（中心）在图形内还是图形外?使用叉乘！），叫做采样。

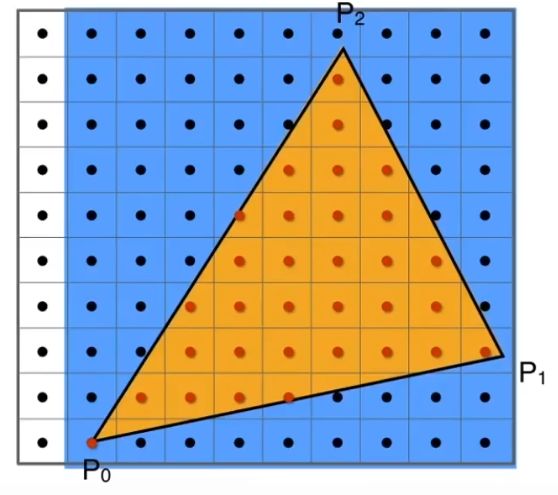
实际充填后会产生锯齿状，产生“走样”。那么如何抗锯齿，反走样呢？

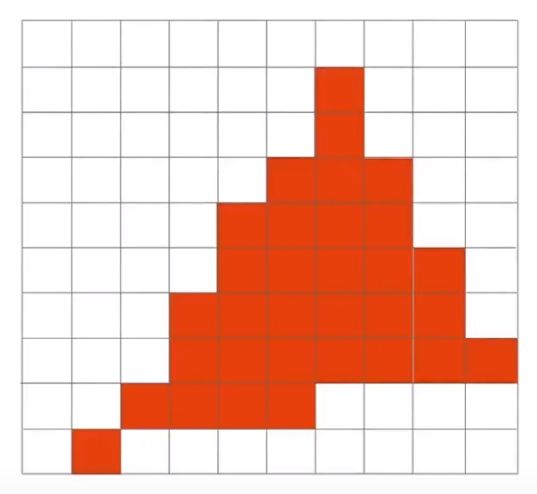
反走样

采样之前先对信号做一次模糊,为什么先模糊再采样能获得更好的效果呢？（先采样再模糊是不行的！）

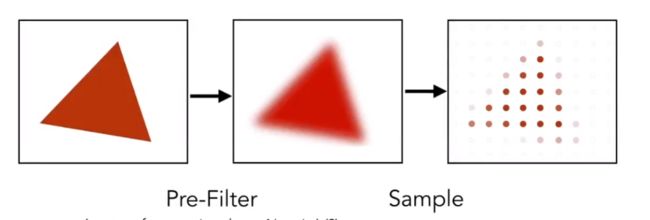
为什么呢？
先说说什么是走样？相同频率下采样，表现出的形态（黑色）可能和实际（蓝色）截然不同。所以需要根据函数的频率进行采样。

时域(Time Domain)是指信号在时间轴上的表现。信号的幅度则是随时间变化的函数。时域信号显示了信号在不同时间点上的变化情况。
频域（frequency domain）是指信号在频率轴上的表现。
频域分析通常通过傅里叶变换或其他频谱分析技术来实现。傅里叶变换将信号从时域转换为频域，将信号表示为不同频率的正弦和余弦波的叠加。频域分析有助于揭示信号中隐藏的频率信息，如频率成分的强度、频率分布等。
下图（右）中，经过傅里叶变化后，中心表示低频，四周表示高频，亮度越高说明信息此频率信息越多（分布越广）。中心比较亮说明这幅照片低频信号较多。为什么会有两条交叉明显光亮的十字星？再做傅里叶变换的时候，认为这张图是上下左右无限重复的，那么对于大多数图片来说，边缘很少出现左右或者上下对称过度的情况，所以图和图之间就会有明显的陡变，产生高频。这些十字星对分析图片内部的信息可以忽略。
滤波：对某些特定的频率的波进行过滤。
下图，对照片中低频率的信号移除，只保留高频率的信号（高通过滤），刚好是照片中重要的轮廓边界信息（高频信息一般位于边界处，因为轮廓经常需要记录陡然变换的高频信号）
再看看低通过滤，对陡变的边界高频信息进行移除，所以边界明显模糊了。滤波=平均=卷积
平均意思是对波的频率按照一定范围进行平均操作，比如低通滤波，也就是模糊的操作，对应一种平均。
卷积，对某个信号周围所有的数，按照滤波器窗口（也是一种特殊的信号，目的是希望Signal经过Filter变化之后，形成一种新的信号）进行点乘相加写到result中间位置，不停对一块区域做这个操作，得到一个新的信号结果。这就是图形学上简化的卷积概念。实际中，卷积的数学上更明确的定义卷积运算：直观理解是将一个函数（g(t)）作为滑动窗口，在另一个函数（f(t)）上进行滑动，并在每个位置上求两个函数的乘积，然后将这些乘积结果叠加得到卷积的输出 h(t)。
经过这些说明，是不是对上述等式已经有了理解。那么这有什么用呢？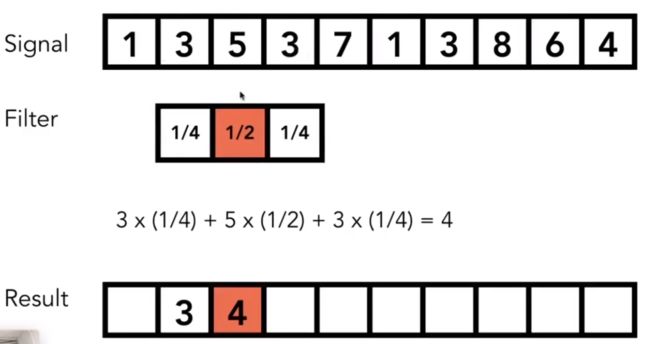
在此之前大家还得再了解一个数学定理–卷积定理：如果 F(ω) 和 G(ω) 分别是信号 f(t) 和 g(t) 的傅里叶变换，那么它们的卷积的傅里叶变换 H(ω) 等于 F(ω) 和 G(ω) 的乘积。
这有什么用呢？前面我们已经说了，一个图形和一个滤波器可以分别作为两个信号，那么这两个信号处理的结果可以理解成两者之间的卷积的结果，是时域上的概念。但是**两者的卷积太难算了！**我们有办法简化下么？对了，刚刚我们已经提到了卷积定理，两个信号的傅里叶变换我们可以轻松得到，那么卷积的傅里叶变化就可以通过卷积定理推出。得到了卷积的傅里叶变化，那么再用一次逆傅里叶变换，就可以得到卷积啦！完美~再不说人话就是，通过这一些列操作，频域（傅里叶变化的结果）和时域（卷积结果）被联系起来了。
时域的卷积=频域的乘积（再做一次逆傅里叶变换）
上图可以看出，滤波器基本都是低频的信息（中心很亮），那么经过它处理的原始信号，得到的新的时域信息（两信号的卷积）， 保留的更多的是低频的信息，所以照片也就越模糊了，这也符合我们的认知。
现在思考下，如果我的滤波器在时域上范围更大，变成9*9的，那么上图中对应的傅里叶变换（下2）应该是怎么样的呢？

结果是低频信息更多。这是因为用更大的“盒子”来平均整个照片，每个像素都被周围更大范围的像素平均，那么肯定会更加模糊的，低频信息也相对更多（更亮了）。

回过头来，再来回顾下什么是采样？

左边1是一个需要被采样的函数，左2是一个采样选择的函数（这个函数间隔一定时间获取y值），两者的卷积就是对应频谱的乘积。所以采样可以理解成重复原始信号的频谱。
走样又怎么理解呢？采样间隔太长，频域上带来的是重复太近，两者发生堆叠，那么这就是走样。

走样的原因知道了，现在说说如何反走样。
方法一：像素越多，采样越密集，增加采样率；

方法二：先把频率高的部分去除，留下低频部分，此时再采样，就不容易发生堆叠了。
实际过程怎么模糊（低频滤波）呢？

把每一个三角形对每一个像素的覆盖率（面积的比值）计算出来，然后进行灰度计算。但这需要大量的工程，覆盖率也不好计算。但可以将一个像素划分成更小的单位，然后根据这些“小像素”的中心是否在三角形中，算出比值做一个覆盖率的近似（MSAA ），达到抗锯齿的效果。它带来的代价增大了计算量。
快速近似抗锯齿（FXAA），得到一个有锯齿的图像，把有锯齿的边界在图片处理阶段直接替换。
实时抗锯齿（TAA），适用于静止的图片，下一帧沿用上一帧的数据。

深度缓冲

经过光栅化实现了一个三角形画在屏幕上，那么怎么实现多个不同深度的三角形都在屏幕上显示，近处的遮挡住远处的呢？
画家算法：和油画家一样，从远至近一层一层将图层画出来。但对于互相遮挡地情况很难处理：

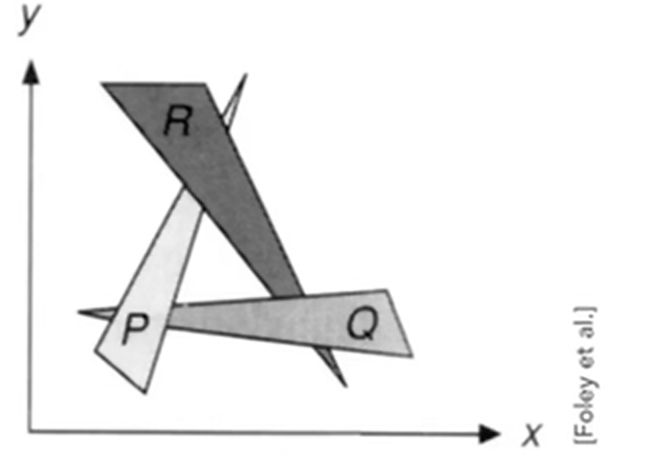
深度缓冲（Z-buffering）
对每个三角形整体很难做排序，但是对每个像素可以进行深浅排序：首先认为每一个像素最初记录的都是无限远的深度；一旦一个新的元素在同一个位置比先前像素记录的z数值更近，那么先显示更近元素的颜色，然后更新该点像素记录的最近z数值；如果更远，则什么都不做。
（R代表无限大）

四、着色

光照与基本着色模型

着色：对不同物体应用不同材质的过程。

Blinn-Phong 反射模型

如图可以看到一些高光、漫反射、间接光照。
（着色是局部的，暂时不考虑周围物体的阴影影响）

漫反射（Diffuse Reflection）

max(0,n·l)：接收能量的比例，介于0-1之间，n和l均为单位向量。漫反射的结果和光照与平面法线之间的夹角有关
kd：如果有颜色，需要再乘以漫反射系数，对光的吸收能力，介于0-1之间
I/r2：到达着色点的能量，光照点着色点的距离r
Ld：漫反射能量

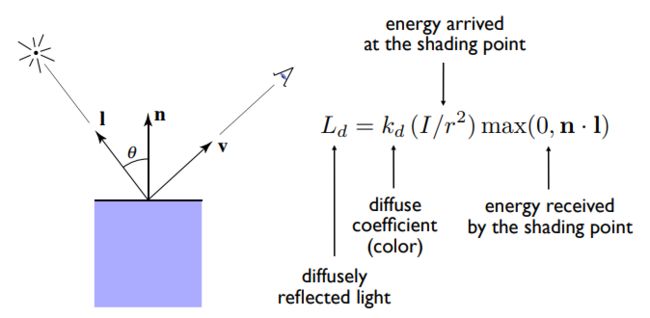
漫反射和v观察角度无关，各个方向均相同。

高光项（Specular Term）

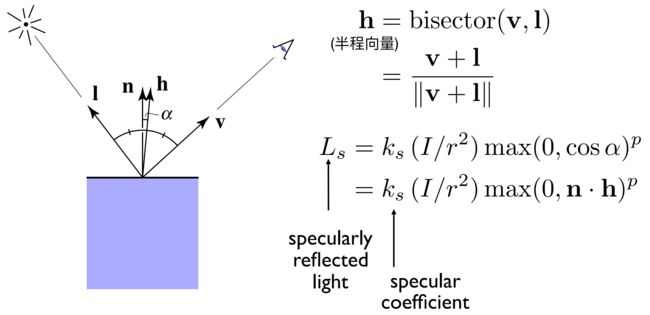
h：半程向量，光线向量和观察向量的叠加后归一为单位向量
max(0,n·h)：接收能量的比例，介于0-1之间，n和h均为单位向量
ks：一般认为为白色，对光的吸收能力，介于0-1之间
I/r2：到达着色点的能量，光照点着色点的距离r
Ls：漫反射能量
p：指数p对夹角余弦进行修订，控制高光的大小的，否则亮面很大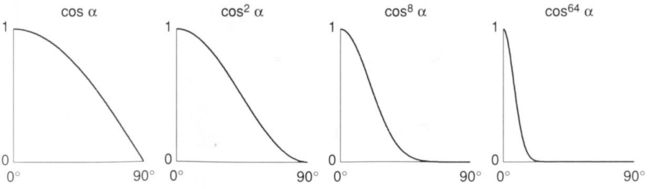
在Blinn-Phong模型中，可以看出ks的增大，增大了高光的亮度；而指数p增大，高光更加聚集。

环境光照（Ambient Term）

环境光照和入射向量观察向量无关，应该是颜色固有的常数。

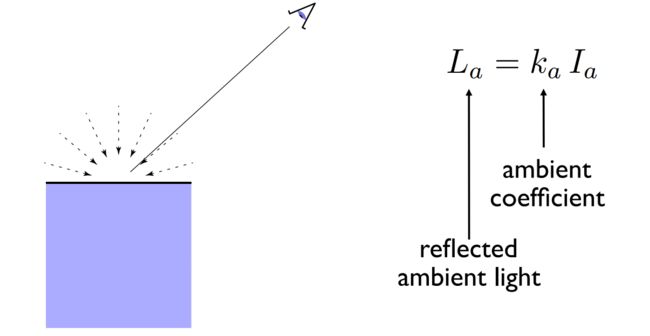
将三个项目得影响聚集起来，可以看到这套理论模型得意义：

着色频率、图形管线、纹理映射

着色频率 Shading Frequencies

Flat shading

图1，逐三角形，对每个三角形计算出法线后，根据上述着色计算公式，可以计算出着色数值，应用在各自的三角形面片中

Gouraud shading

图2，逐顶点，对每个三角形顶点找到法线后，应用着色计算公式，之后对三角形内部进行插值着色。
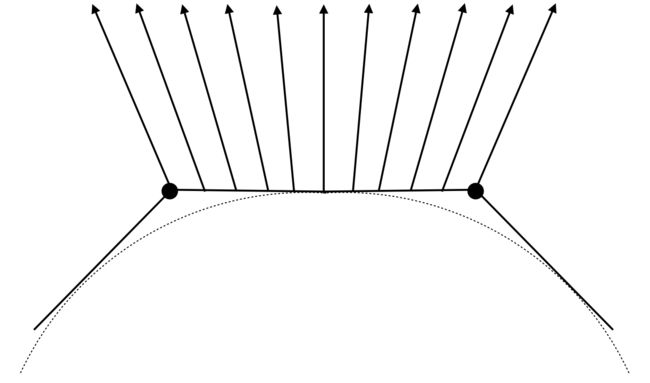
顶点的发现怎么计算？

如果近似圆，过圆心朝外即为每个顶点的法向量，普通的图形，使用顶点周围所有平面的法向与面积比的加权，为顶点法向量。

Phong shading

图3，对每个像素进行着色

图形管线

图形管线（Graphics Pipeline- Real Time Render）：三维数据经过MVP可以抽象成三维空间的顶点，顶点经过投影变成二维数据离散的点；点之间的连接关系并没有变化，连接生成三角形；对图形进行光栅化；光栅化后再进行着色处理。如果使用的顶点着色的方法，再图形处理管线流程中，顶点投影的同时也进行顶点着色处理，如果用的是Phong处理每一个像素的着色，那么就正常流程处理至着色阶段再处理每个像素即可。

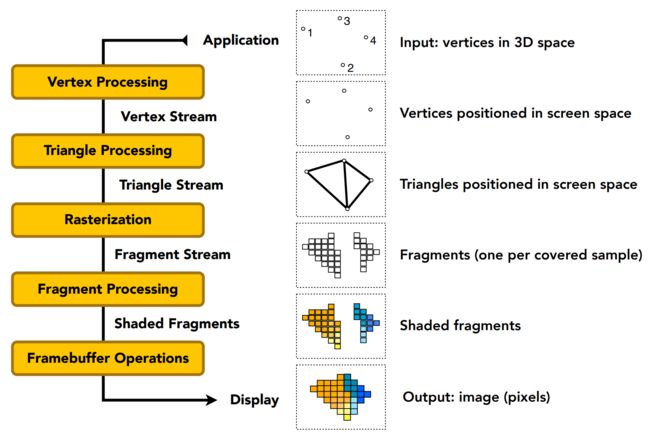
如何训练shader？可以通过shadertoy了解一些写好的例子：shadertoy官网

纹理映射

纹理映射（Texture Mapping）：纹理就是一张图，通过任意截取拉伸或压缩等操作，然后蒙在三维实体的表面上，就是纹理。主要是为了在物体不同位置展现不同的属性。

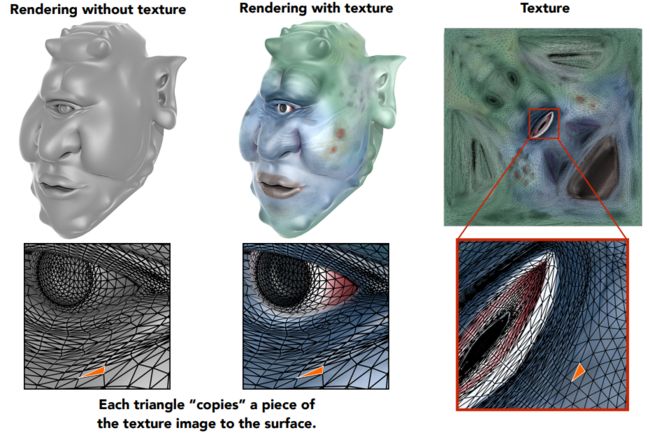
任何三维物体的表面都是平面，空间三角形最终可以转换到平面的三角形上。在贴图的过程中：如果能保证众多三角形在展开的时候尽可能少的扭曲，相对大小最好不变，如果在三维上无缝衔接的表面，二维的纹理如果也能满足，那就是很好的纹理。这部分称为参数化，不需要我们考虑空间中的三角形映射到平面上，通过已有的技术可以获取三维的三角形在二维纹理上对应的坐标。

纹理的坐标系：无论纹理本身是否是方块，uv均规定在（0,1）之间。空间三角形每一个顶点均对应一个uv（那么三角形内部的点如何设置属性呢？之后在重心坐标的内容会提及，如何使用插值将三角形内部属性平滑地表现出来）。

Tileable Textures，可以实现纹理的无缝连接，典型的Wang Tiling。

纹理和着色的关系：纹理定义着色时候各个点的属性。

插值、高级纹理映射

着色插值

如何在三角形内部插入坐标：重心坐标（Barycentric Coordinates）–在三角形ABC内部，任意一个点地xy坐标都可以满足三个顶点坐标的线性组合，其中线性组合的系数相加为1（无论是在什么类型的坐标系下），否在不在三角形所在平面内。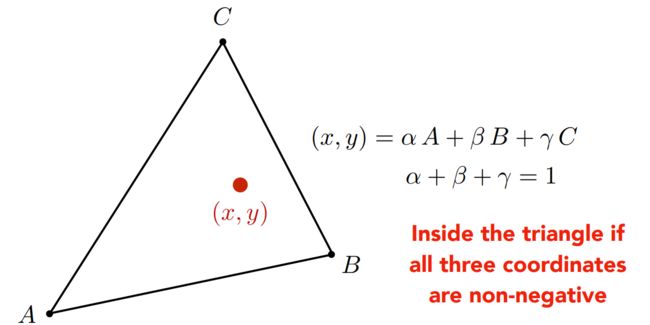
其中如果在三角形内部，αβγ均为非负，三角形上所有点都可以用这三个系数表示出来，如三角形ABC，A（1，0，0）B（0，1，0）C（0，0，1）

---

总结