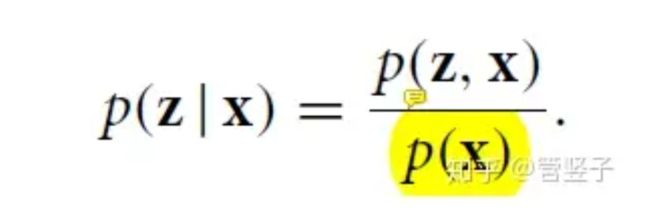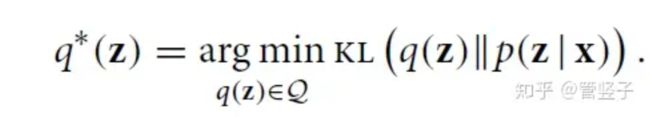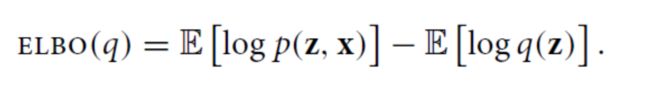https://arxiv.org/abs/1711.00937
直接3.1
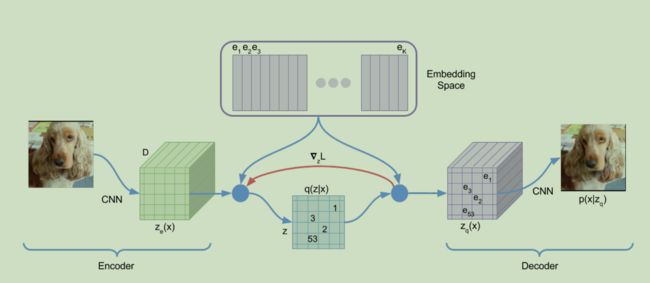
首先我们定义一个嵌入空间. 是K*D维度的. K是离散空间向量的数量. D是每一个向量的维度.
所以e_i 中的i属于 1到K.
模型的输入是x, 也就是图片. 然后模型编码成一个z_e(x). 然后使用最近算法来得到 z_q
具体公式是下面1和2.
理解q这个分布.
给定x之后, 是一个0,1 离散分布. 对于下表 i 属于1到K进行分布. i 等于 最接近 z_e=ej时候取1, 其他时候取0.
![]()
第一项代码里面是mse用来更新embedding里面的参数. (具体就是图片x 给定, x找到索引i, 然后i从embedding_sapce里面计算出z_q, 后续生成xhat, 所以学习之后的结果是embedding和decoder里面参数进行了更新,让索引i找到的向量很能最后生成xhat趋近于x)
第二项是用来训练encoder的. 从上面第一项分析看得出来, encoder参数没法更新. 所以这里面我们设计让z_e趋近于e, e是embedding得到的向量, 也就是我们如果训练完得到的z_q. 这样我们的损失也可以让encoder来学习参数了.
第三项是让每次z_q和z_e不要变化太大. 利于网络收敛.
P概率定义如下.
变分推断--理解变分推断中的ELBO
z是隐变量. 用来生成x
下面这个条件概率是我们需要的. 知道这个概率之后,我们就可以知道给定x, 之后z 取什么值概率最大了. 之后我们直接取概率最大的那个z值作为隐变量即可.
如果我们用一个分布q(z)来你和上面分布. 那么需要
所以我们优化p, 就可以改为优化elbo(q).
https://blog.csdn.net/Jimmy_dovici/article/details/127739578 这个讲的很好
后验概率分布是一个未知量(视为随机变量)基于试验和调查后得到的概率分布 . 也就是我们最后要的终极目标
先验概率是未知量调查前的概率分布
似然:是我们的刻画函数. 正面思维能真正获得的函数.
看elbo:
给定一个observation variable x xx(比如RGB图片)和latent variable z zz(比如是RGB图片经过encoder得到的latent feature),假设我们想学习后验概率p ( z ∣ x ) ,但发现p ( z ∣ x ) 在实际中不易或不能求解,那么该如何求解这个后验概率?
————————————————
版权声明:本文为CSDN博主「科研小呆瓜」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/Jimmy_dovici/article/details/127739578
那么我们要做的其实就是最大化E L B O ( q ) \mathrm{ELBO}(q)ELBO(q) ,
所以损失函数是. E_q(log_q)- E_q(logp(x,z))