图应用之最短路径问题(头歌教学实践平台)
第1关:最短路径问题
任务描述
本关任务:编写代码完成 Dijkstra 算法的 Python 实现,解决图的最短路径问题。
相关知识
为了完成本关任务,你需要掌握: 1.什么是最短路径问题; 2.如何利用 Dijkstra 算法来解决最短路径问题。
最短路径问题
当我们通过网络浏览网页、发送电子邮件、QQ 消息传输的时候,数据会在联网设备之间流动。如图 1 所示,当 PC 上的浏览器向服务器请求一个网页时,请求信息将先通过本地局域网,由路由器 A 发送到 Internet,随后请求信息沿着 Internet 中的众多路由器传播,最后到达服务器本地局域网所属的路由器 B,从而传给服务器。
图1 互联网连接概览
图 1 中标注“Internet”的云状结构,实际上是一个由路由器连接成的网络。这些路由器各自独立而又协同工作,负责将信息从 Internet 的一端传送到另一端。通过路径跟踪指令可以看到信息传送过程中所经过的路由器。如果你在同一天中的不同时间段执行路由跟踪指令,很有可能发现发送的信息在不同的时间经过了不同的路由器。这是因为任何两个路由器之间的连接都不是没有代价的,而是受线路拥挤情况、时间以及许多其他因素的影响。
我们可以将互联网路由器体系表示为一个带权边的图,路由器作为顶点,路由器之间网络连接作为边,权重可以包括网络连接的速度、网络负载程度、分时段优先级等影响因素。作为一个抽象,可以把所有影响因素合成为单一的权重,如下图 2 所示。
图2 互联网路由器之间的连接和权重
我们所要解决的最短路径问题是找到一条总权重最小的路线,并且使之实现传递任何信息的功能。这个问题与用广度优先搜索算法解决的词梯问题很相似,区别在于现在要考虑的是整条路线的总权值,而不是路线中的顶点数。需要特别注意的是,如果所有边的权值都相等,那么这两个问题是等价的。
Dijkstra 算法
解决带权最短路径问题的算法被称为 Dijkstra 算法。Dijkstra 算法是一 种迭代算法,用来得出从一个顶点到其余所有顶点的最短路径,这与广度优先搜索 BFS 的结果很类似。
为了追踪从开始顶点到每一个结束顶点的总权值,我们将在顶点 Vertex 类中使用 dist 实例变量,用于记录从开始顶点到本顶点的最小权值路线的当前总权值。即对 Vertex 类进行扩展完善,在该类中加入 dist 实例变量,并初始化为最大整数 sys.maxsize,同时定义了相应的设置方法setDistance和取值方法getDistance。又因为在算法中会利用前驱顶点来得到最短路径,同时也需在类中加入前驱 pred 实例变量。代码示例如下:
class Vertex:def __init__(self,num):……self.dist = sys.maxsize # 距离 distself.pred = None # 前驱def setDistance(self,d): # 设置 distself.dist = ddef setPred(self,p): # 设置前驱self.pred = pdef getDistance(self): # 获取 distreturn self.distdef getPred(self): # 获取前驱return self.pred……
Graph 和 Vertex 类的相关知识请参考图抽象数据类型的 Python 实现。
对于图中的每一个顶点,算法均会重复进行一次。各顶点重复的先后顺序由一个优先队列来控制,队列中决定顺序的参量是顶点的 dist 值。优先队列的出队(Dequeue)操作和队列一样,都是从队首出队。但在优先队列内部,数据项的次序是由它们的“优先级”来确定的:有最高优先级的数据项排在队首,而优先级最低的数据项则排在队尾。
在 Dijkstra 算法中,我们以顶点间距离 dist 来决定优先级,在探索下一个顶点时,总是选择最小距离的顶点。这样,优先队列的入队(Enqueue)操作就可能需要将数据项挤到队列前方。在这里,我们采用二叉堆的数据结构来实现优先队列,其基本操作定义如下:
- PriorityQueue():创建一个新的空优先队列(二叉堆)对象
- buildHeap(list):从一个 key 列表创建新堆
- insert(k):加入一个新数据项到堆中
- findMin():返回堆中的最小项,最小项仍保留在堆中
- delMin():返回堆中的最小项,同时从堆中删除
- isEmpty():返回堆是否为空
- decreaseKey(val,amt):顶点 val 的 key 改变为 amt,并对堆进行重新调整
优先队列的相关知识请参考二叉堆实现的优先队列。但简单的优先队列实现与 Dijkstra 算法中的优先队列实现有一些不同,为了求最短路径,在优先队列 PriorityQueue 类中添加了decreaseKey方法,当队列中某个顶点的距离 dist 减小的时候,将会对这个顶点进行调整,在堆中上浮到最终正确的位置。
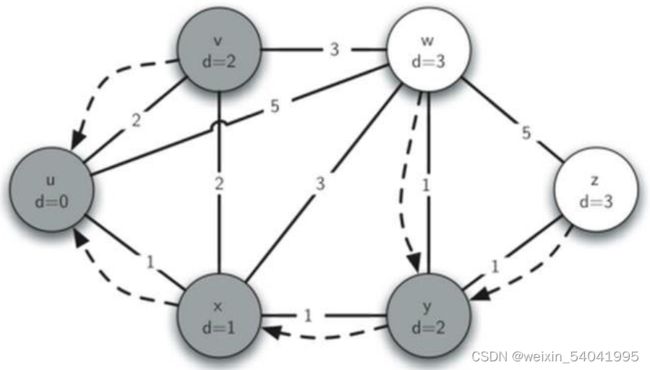
下面为 Dijkstra 算法的一个应用实例,该实例以 u 为开始顶点。最初,只将开始顶点 u 的 dist 设置为 0,而其他所有顶点的 dist 都设置为最大整数 sys.maxsize,并且全部加入到优先队列中。与 u 相邻的三个顶点是 v、w 和 x,算法最开始从 u 到这三个顶点的距离都小于对应 dist 初始的最大整数 sys.maxsize,所以更新这三个顶点的距离值 dist 分别为 2、5 和 1。同时,将每个顶点的前驱顶点都设置为 u,并且以距离来更改每个顶点在优先队列中顺序。算法当前状态如图 3 所示,在图中用 d 表示顶点的 dist,用虚线来指向当前顶点的前驱顶点。
图3 检查与 u 相邻的顶点
接下来使用 while 循环来检查与 x 相邻的顶点。之所以先选择 x ,是因为 x 的 dist 最小,位于优先队列的顶端。与 x 相邻的顶点有 u、v、w 和 y。对于每一个相邻的顶点,我们要检查经由 x 顶点到当前顶点的距离 dist 是否小于已知的距离 dist。
-
顶点 u 和 v 不满足条件,因为它们各自的原始 dist 是 0 和 2,而经由 x 再到 u 和 v 的距离都要比原始 dist 大;
-
经由 x 到 w 的距离小于直接从 u 到 w 的距离,因此需要更新 w 的距离值为经过 x 到 w 的距离 4,并将 w 的前驱顶点从 u 改为 x;
-
y 的原始 dist 是 sys.maxsize,明显满足条件,更新 y 的 dist 为经过 x 到 y 的距离 2,并将 y 的前驱顶点设置为 x。
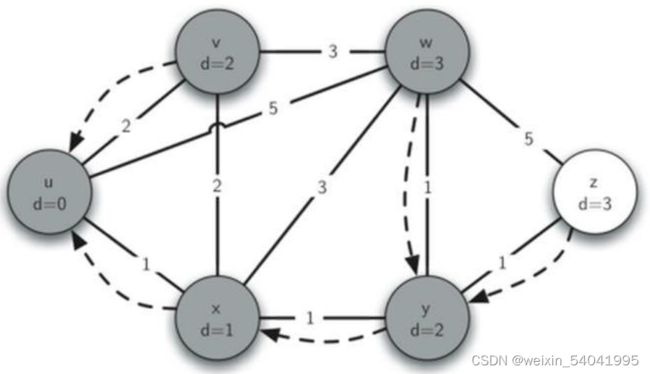
算法当前状态如图 4 所示。
图4 检查与 x 相邻的顶点
根据优先队列中的最小 dist,下一步是检查与 v 相邻的顶点。由于经过 v 再到达 w 的距离为 2+3=5,大于 w 此时的 dist 值 4,因此无需修改,这一步对图并无更新操作,算法当前状态如图 5 所示。
图5 检查与 v 相邻的顶点
根据优先队列中的最小 dist,下一步是检查与 y 相邻的顶点。
-
对于 w 来说,经过 y 再到达 w 的距离为
2+1=3,小于 w 原始的 dist 值 4,因此更新 w 的 dist 为更小的值 3,修改 w 的前驱为 y; -
对于 z 来说,经过 y 再到达 z 的距离为
2+1=3,小于最开始对 z 的 dist 初始化的最大整数 sys.maxsize,因此更新 z 的 dist 为更小的值 3,修改 z 的前驱为 y。
算法当前状态如图 6 所示。
图6 检查与 y 相邻的顶点
随后检查顶点 w,经过 w 到达其相邻顶点 z 的距离为 3+5=8,大于 z 原始的 dist 值 3,所以无需修改,这一步对图并无更新操作,算法当前状态如图 7 所示。
图7 检查与 w 相邻的顶点
随后检查顶点 z,同样也没有需要修改的地方,Dijkstra 算法结束,当前状态如图 8 所示。
图8 Dijkstra 算法结束
Dijkstra 算法实现的步骤可总结为:
- 将开始顶点的 dist 设为 0, 而其他所有顶点 dist 设为最大整数 sys.maxsize,全部加入优先队列;
- 将队列中每个最小 dist 顶点率先出队;
- 计算它与邻接顶点的权重,判断是否会引起其它顶点 dist 的减小和修改,有改变则进行堆重排;
- 根据更新后的 dist 优先级再依次出队,重复第 2、3 步,直到所有顶点访问完。
编程要求
在右侧编辑器中的 Begin-End 区间补充代码,根据 Dijkstra 算法的算法思想和所展示出的优先队列 PriorityQueue 类,完成dijkstra方法,求出有向赋权图的最短路径。
测试说明
平台会对你编写的代码进行测试,比对你输出的数值与实际正确的数值,只有所有数据全部计算正确才能通过测试:
测试输入:
5,0 1 3,0 4 6,1 2 4,1 4 1,2 3 3,4 2 2
输入说明:输入字符串第一个逗号前的数值表示所创建的有向图的顶点数,剩下的部分同样以逗号进行分隔。分隔成的每一小段又以空格分隔成三部分,分别表示所添加边的第一个顶点、第二个顶点以及边上的权值。
预期输出:
01423
输出说明:输出为对所创建图通过 Dijkstra 算法求出的从顶点 0 到顶点 3 的最短路径顶点序列。
测试输入:
6,0 1 5,0 5 2,1 2 4,2 3 9,3 4 7,3 5 3,4 0 1,5 4 8,5 2 1
预期输出:
0523
开始你的任务吧,祝你成功!
'''请在Begin-End之间补充代码, 完成dijkstra函数'''
class PriorityQueue:
def __init__(self):
self.heapArray = [(0,0)] # 初始化一个列表,用来保存堆数据
self.currentSize = 0 # 用来跟踪记录堆当前的大小
# 从无序表建立一个堆
def buildHeap(self,alist):
self.currentSize = len(alist)
self.heapArray = [(0,0)]
for i in alist:
self.heapArray.append(i)
i = len(alist) // 2
while (i > 0):
self.percDown(i)
i = i - 1
def percDown(self,i):
while (i * 2) <= self.currentSize:
mc = self.minChild(i)
if self.heapArray[i][0] > self.heapArray[mc][0]:
tmp = self.heapArray[i]
self.heapArray[i] = self.heapArray[mc]
self.heapArray[mc] = tmp
i = mc
# 求出最小子结点
def minChild(self,i):
if i*2 > self.currentSize:
return -1
else:
if i*2 + 1 > self.currentSize:
return i*2
else:
if self.heapArray[i*2][0] < self.heapArray[i*2+1][0]:
return i*2
else:
return i*2+1
# 不断交换,直到新结点“上浮”到正确位的置来保持堆次序
def percUp(self,i):
while i // 2 > 0:
if self.heapArray[i][0] < self.heapArray[i//2][0]:
tmp = self.heapArray[i//2]
self.heapArray[i//2] = self.heapArray[i]
self.heapArray[i] = tmp
i = i//2
# 添加新的的数据
def add(self,k):
self.heapArray.append(k)
self.currentSize = self.currentSize + 1
self.percUp(self.currentSize)
# 移走堆中的最小项
def delMin(self):
retval = self.heapArray[1][1]
self.heapArray[1] = self.heapArray[self.currentSize]
self.currentSize = self.currentSize - 1
self.heapArray.pop()
self.percDown(1)
return retval
# 返回堆是否为空
def isEmpty(self):
if self.currentSize == 0:
return True
else:
return False
# 结点 val 的 key 改变为 amt,并对堆进行重新调整
def decreaseKey(self,val,amt):
done = False
i = 1
myKey = 0
while not done and i <= self.currentSize: # 找到顶点val
if self.heapArray[i][1] == val:
done = True
myKey = i
else:
i = i + 1
if myKey > 0:
self.heapArray[myKey] = (amt,self.heapArray[myKey][1])
self.percUp(myKey)
def __contains__(self,vtx):
for pair in self.heapArray:
if pair[1] == vtx:
return True
return False
def dijkstra(aGraph,start):
pq = PriorityQueue()
start.setDistance(0) # 开始顶点的距离设为0
pq.buildHeap([(v.getDistance(), v) for v in aGraph]) # 对所有顶点建堆,形成优先队列
while not pq.isEmpty(): # 当优先队列不为空时做以下操作
# 从优先队列中出队一个顶点作为currentVert
# ********** Begin ********** #
currentVert = pq.delMin()
# ********** End ********** #
for nextVert in currentVert.getConnections(): # 遍历与当前顶点相邻的顶点
newDist = currentVert.getDistance() + currentVert.getWeight(nextVert) # 求出新的距离
# 若新的距离值小于之前的距离值,就更新
# 更新距离
# 设置前驱顶点
# ********** Begin ********** #
if newDist < nextVert.getDistance():
nextVert.setDistance(newDist)
nextVert.setPred(currentVert)
# ********** End ********** #
pq.decreaseKey(nextVert, newDist) # 优先队列重排