2019_WWW_Dual graph attention networks for deep latent representation of multifaceted social effect

[论文阅读笔记]2019_WWW_Dual graph attention networks for deep latent representation of multifaceted social effects in recommender systems—(The World Wide Web Conference, 2019.05)-- Qitian Wu, Hengrui Zhang, Xiaofeng Gao, Peng He, Paul Weng, Han Gao, Guihai Chen

论文下载地址：https://dl.acm.org/doi/abs/10.1145/3308558.3313442
发表期刊：The World Wide Web Conference
Publish time: 2019.05
作者单位：上交，腾讯
数据集：

• Epinios,
• Wechat Top story

代码：https://github.com/echo740/DANSER-WWW-19

本文最大的创新(贡献)–个人的理解

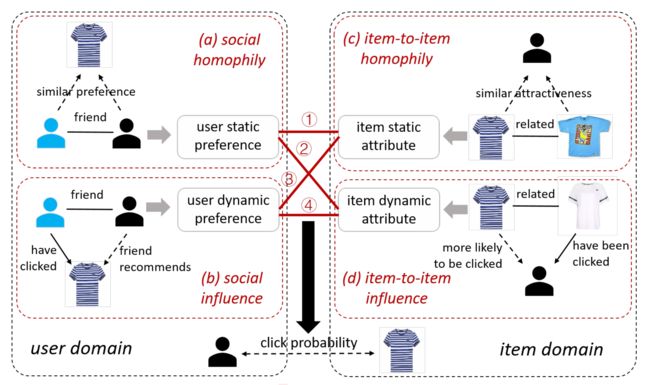
• (1) 对user或item，从2个方面考虑的：
  一是：homophily，它global的，是static的
  (就是想找一个东西，代表自己的inherent的一些东西)
  二是：influence，它是local的，是dynamic的
  (就是想找一个东西，代表在自己可选可不选的时候，会被其他uer影响的情形)
• (2) 是context-awared的(a context is a user item pair)
  个人理解，context aware本身就是作者自己定义的。就像马哲里说的，就是一个具体的情形(specific condition)
  作者用Dual GAT 去学习two-fold social effects的权重参数
• (3)采取一个有效的策略(方法，机制，流程)，对这4种interactions进行fuse，因为到最后总要利用这些信息得到一个结果
  作者propose a new policy-based fusion strategy based on contextual multi-armed bandit(多臂老虎机，这个就是强化学习RL的内容，感觉现在趋势就是多种方法一起用，融合)

Abstract(本文的创新点)

(1) However, most existing models assume that social effects from friend users are static and under the forms of constant weights or fixed constraints.
(2) To relax this strong assumption, in this paper, we propose dual graph attention networks to collaboratively learn representations for two-fold social effects, where one is modeled by a user-specific attention weight and the other is modeled by a dynamic and context-aware attention weight
(3) we propose a new policy-based fusion strategy based on contextual multi-armed bandit to weigh interactions of various social effects

1 Introduction

1.1 Prior Works and Limitations

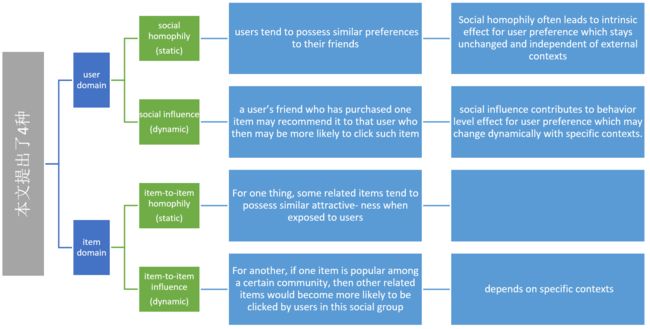
(1) First, most studies assume that linked users all share similar preferences. This assumption cannot suit well contemporary SNS since there could be various types of online friends, such as close friends, casual friends, and event friends.（朋友分很多种）
(2) Second, most works model friends’ influences statically under the forms of constant weights or fixed constraints. This assumption ignores the dynamic pattern of social effects.（忽略了社会影响的动态模式）
(3) Third, previous methods lack interpretability for social effects

1.2 Motivations and Rationales

Figure 1: Illustration of the two-fold social effects, i.e., homophily effect and influence effect, in user social networks as well as among related items. The four social effects jointly affect a user’s decision on one item. In this paper, we aim to build an unfied model to represent and weigh four effects given different user-item pairs.

1.3 Methodologies and Results

(1) we propose DANSER (Dual graph Attention Networks for modeling multifaceted Social Effects in Recommender systems)

(3) such dual mechanism possesses two advantages:

(4) we propose a policy-based strategy to dynamically weigh the four interactions.
Specifically, we model the problem as a contextual multi-armed bandit, and treat the weighing strategy as a policy conditional on the context (the targeted user-item pair). Then our goal is to optimize a reward (w.r.t predicted loss)
(5) For model training, we use stochastic policy gradient to update our neural network-based policy unit, and design a local-graph aware regularization technique to reduce computational cost for regularization

(6)数据集
Epinions
WeChat Top Story

1.4 Our Contributions（与上面重复，但算是一个小总结）

1.4.1 General Aspects

We distinguish the social homophily and social influence notions in view of static and dynamic effects. Also, we extend the two-fold social effects in user domain to item domain, and therefore investigate four social effects in recommender systems

1.4.2 Novel Methodologies

We propose DANSER with two dual GATs and a policy-based fusion unit. The dual GATs can collaboratively model four social effects in both user and item domains, while the policy unit, based on a contextual multi-armed bandit, dynamically weighs four interactions of social effects in two domains according to specific contexts

1.4.3 Multifaceted Experiments

2 Preliminary and Background

$R_i(u)$ denote the set of items rated by user $u$
$R_u(i)$ denote the set of users who have rated item i
$F_u(u)$ denote the set of nodes adjacent to $u$ in $G_u$
user-item interaction matrix $R$
user social network $G_U$

Problem Formulation

3 Methodologies

3.1 Model Framework

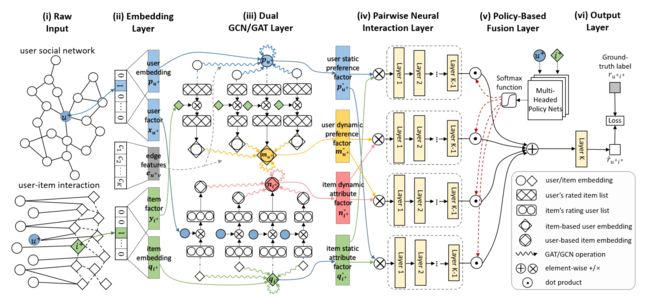
Figure 2: DANSER framework. Blue circles denote a targeted user $u^{+}$ while green rhombuses denote a candidate item $i^{+}$. i)
The model requires user-item interaction records and user social network as raw input. We use common users who rate both items to calculate the item-item relevance and link the related items to form an item implicit network (the dotted lines be- tween items). ii) In the embedding layer, we represent one user (resp. item) as a low-dimensional embedding vector and a latent factor. Besides, interaction frequencies between users are used as edge features. iii) In the dual GCN/GAT layer, four different graph attention networks are to capture the two two-fold social effects, where the upper (resp. lower) two of them output representations for user (resp. item) static and dynamic preferences (resp. attributes) under the effect of homophily and influence, respectively. iv) These four deep factors will be pairwisely combined as four interacted features, which are then fed into four independent neural networks to obtain more condensed representations. v) Then a policy net with the input of item $i^{+}$’s and user $u^{+}$’s embeddings as context information outputs weights for four interacted features, which will be aggregated as one synthetic vector. vi) Finally, the synthetic vector is input into the output layer to give the final predicted score ${\hat{r}}_{u^{+}{i}^{+}}$.

3.3.1 Raw Input and Item Implicit Network

(1) Most existing methods treat items independently since there is no prior information that explicitly expresses the relationship between items
(2) One way to calculate the similarity or relevance between two items is by the common users who clicked or rated them . For any item $i$ and item $j$, we define their similarity coefficient $S_{ij}$ as the number of users who clicked both items. These coefficients induce an equivalence relation over items as follows: item $i$ is related to item $j$ if $S_{ij}>\tau$ with $\tau$ a fixed threshold. （物品间的相似度，可以用共同rate它们的user数量来定义）
(3) We define the item implicit network as the graph $G_I=(V_I,E_I)$ where $V_I$ is the set of items and $E_I$ is the set of edges that connects two related items.

3.1.2 Embedding Layer

(1) The raw input of each user (resp. item) is a one-hot vector with high dimension, and the embedding operation is to project each user to a low-dimensional representation

3.1.3 Dual GCN/GAT Layer

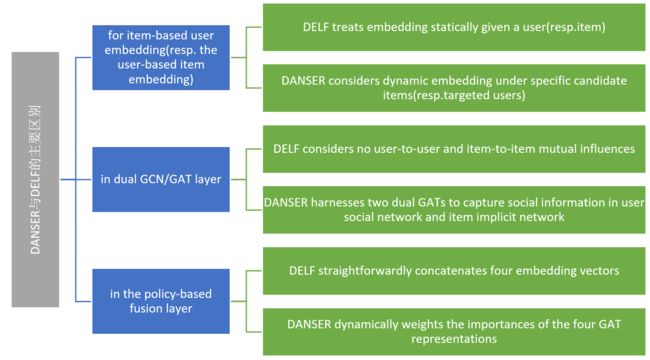
(1) 说一下GCN GAT在干嘛，能干嘛（GCN GAT特性，是前人的工作）
Graph convolution network (GCN) conducts local convolutional operation over neighbor nodes in graph and outputs a new representation for each node, in order to encode the graph structure information as low-dimensional node representations. Such operation can be viewed as an extension of convolution neural network (CNN) from a grid structure to general graphs. GCN equally aggregates the neighbors’ embedding in each convolution and treats each neighbor nodes with equal importance. In contrast, Graph Attention Network (GAT) [31] leverages attention mechanism to consider different weights from neighbor nodes, which enables the model to filter out noises and focus on important adjacent nodes.
(2) DANSER uses two dual GATs to collaboratively learn different deep representations for user static/dynamic preference and item static/dynamic attribute

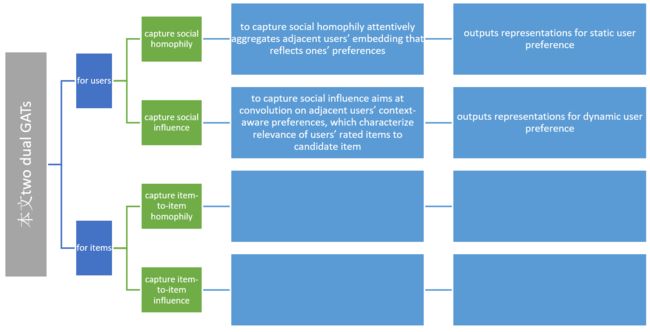
(I) GAT to capture social homophily (marked as blue in Fig. 2).

(1) via user embedding, we have $P$ as representation of inherent user preference factor.
Then the GCN/GAT operation could output a new representation, the user static preference factor $P^{\ast }$

Where $\sigma$, $W_p$, $b_p$ are activation function, weight matrix, bias vector respectively, and $P^{\ast }$ is the updated representation of users, which incorporates social information by using the attention weights. $A_p(G_U)=\{{\alpha }_{UV}^P{\}}_{M\times N}$ obtained from $G_U$. Its elements are defined as follows

where $W_E$ is weight matrix, ${\Gamma }_U(u)=\{u\}\cup F\{u\}$, $att{n}_U(x,y,z)=LeakyRelu(w_U^{T}z\otimes (x\parallel y))$, and $w_U$ is weight vector. Here $\otimes$ and $\parallel$ denote the element-wise product and concatenation, respectively.
Note that the above GAT weight ${\alpha }_{uv}^P$ remains unchanged given user $u$ and $v$, which means factor matrix $P^{\ast }$ is fixed for users

(II) GAT to capture social influence (marked as yellow in Fig. 2)

(1) In contrast to social homophily, social influence effect is often context-aware, and the model needs to output different attention weights for friends w.r.t different candidate items
(2) Through the embedding layer, we have $y_u$ as the embedding of the items clicked by user $u$. Then we let each item clicked by user $u$ interact with candidate item $i^{+}$

(3) This product operation can help to focus on the candidate item and model dynamic social influence under a specific context. We define the item-based user embedding $M_{i^{+}}=\{m_u^{i^{+}}{\}}_{D\times M}$ which depends on candidate item $i^{+}$ with max pooling to select the most dominating features for D dimensions

where $m_{ud}^{i^{+}}$, $y_{i^{+}d}$, and $y+jd$ are the d-th feature of $m_u^{i^{+}}$, $y_{i^{+}}$, $y_j$ respectively.
(4) The max pooling operation can help to focus on the most important value and alleviate noises in users’ clicked history.
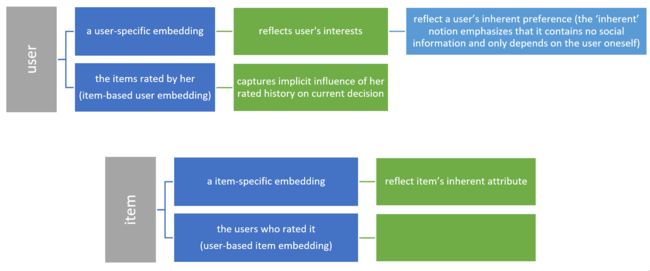
(5) The item-based embedding $m_u^{i^{+}}$ includes two information: i) user $u$’s context-aware preference (w.r.t candidate item i+), and ii) inherent representation for $u$ (independent of social information).
(6) In order to define the user dynamic preference factor $M_{i^{+}}^{\ast }$, we proceed to incorporate the social information from friend users,

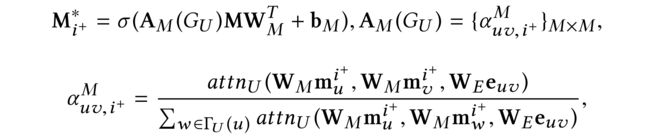
for $v\in {\Gamma }_U(u)$. Note that the above attention weight ${\alpha }_{uv,i^{+}}^M$ depends on the user’s history of rated items as well as specific candidate item $i^{+}$, which indicates that factor matrix $M_{i^{+}}^{\ast }$ would change dynamically with different contexts.

(III) GAT to capture item-to-item homophily (marked as green in Fig. 2)

Similarly, we use the item embedding Q as representation of inherent item attribute factor, and then leverage GAT to incorporate social information

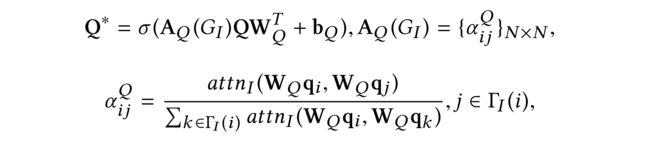
where $att{n}_i(x,y)=LeakyRelu(w_I^T(x\parallel y))$, and $w_I$ is a weight vector. The GAT weight ${\alpha }_{ij}^Q$ remains unchanged given item $i$ and $j$.
Correspondingly, item-to-item homophily contributes to static effect for item’s attribute, and we call it static attribute factor.

(IV) GAT to capture item-to-item influence (marked as red in Fig.2)

We now model item-to-item influence, which is context-aware and depends on the specific targeted user. Hence, our model needs to output different attention weights for distinct related items w.r.t different targeted users. Similarly to social influence, the user-based item representation $N_{u^{+}}=(n_i^{u^{+}}{)}_{D\times N}$ for a given targeted user $u^{+}$ can be defined as follows:

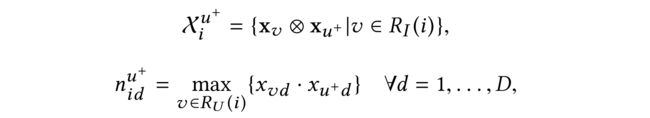
where $n_{id}^{u^{+}}$, $x_{u^{+}d}$, and $x_{vd}$ are the $d$-th feature of $n_i^{u^{+}}$, $x_{u^{+}}$, $x_v$ respectively.
Then the representation for item dynamic attribute $N_{u^{+}}^{\ast }$ can be computed as follows:

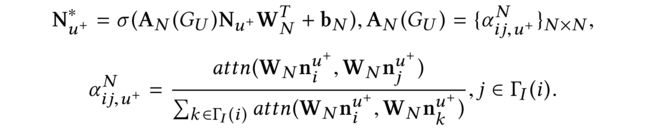
3.1.4 Pairwise Neural Interaction Layer

Since user’s decision on one item often depends on both user preference and item attribute feeding the four results into different neural networks indexed by a∈ {1, 2, 3, 4}

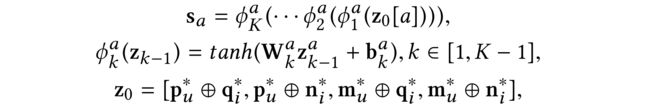
Here we employ a tower structure for each network, where higher layers have smaller number of neurons(DELF中就是这样做的)

3.1.5 Policy-Based Fusion Layer

(1) we propose a new policy-based fusion strategy to dynamically allocate weights to the four interacted features according to specific user-item pairs
We model the weight allocation as a contextual multi-armed bandit problem, where an action, denoted by γ ∈ {1, 2, 3, 4}, indicates which feature to choose, a context is a user-item pair and the reward after playing an action represents a recommendation loss
(2) In this problem, a stochastic policy can be written as the conditional probability $p(\gamma |p_u,q_i)$
(3) To make the problem solvable, we approximate by a neural network (called policy network):

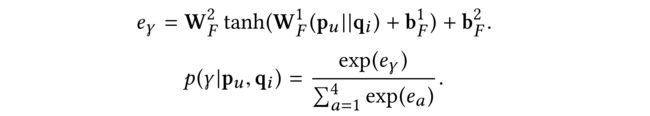
Then the synthetic representation can be expressed as

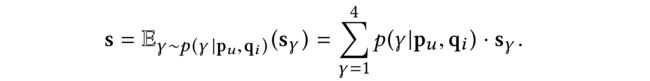
We call the above strategy single-headed policy-based fusion(单头基于策略的混合)
we can extend it to a multi-headed version. We harness L different independent policy networks and the final weights are given by the averaged weights given by each policy net. The training of policy networks is by stochastic policy gradient

3.1.6 Output Layer

Then probability of user u clicking item i can be predicted by
$${\hat{r}}_{ui}=nn(s)$$
(1) If a clicking probability is required (for implicit feedback), $nn(\cdot )$ can be a fully-connected layer with a sigmoid activation function
(2) If a rating value is needed (for explicit feedback), $nn(\cdot )$ can be a fully-connected layer without activation function

3.1.7 Loss Function

(1) For implicit feedback, the most widely adopted loss function is the cross-entropy defined as

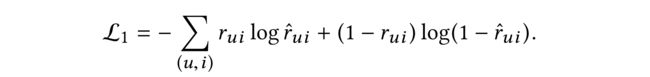
(2) For explicit feedback, we adopt the mean square loss

3.2 Training

3.2.1 Mini-Batch Training.

We also leverage mini-batch training to calculate the gradient
We observe that number of friends tends to obey a long-tail distribution

3.2.2 Local-Graph Aware Regularization

(1) In our model, we adopt L1 regularization to constrain the embedding parameters to sparse forms. The regularization loss can be expressed as

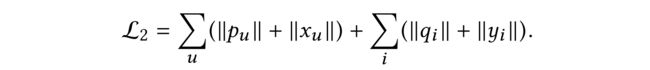
In each batch training, only the embedding parameters for user-item pair $(u,i)$ in the batch will be used to calculate the regularization loss. Here we extend this idea to graph structure and call it as local-graph aware regularization. The new regularization loss can be written as

To sum up, the final loss function is

(2) Besides, for parameters in neural networks (weight matrix and bias vectors), we adopt dropout strategy to replace the traditional regularization

3.2.3 Policy Gradient

(1) In training stage, we train the policy networks in a stochastic way
(2) The policy gradient method REINFORCE can be used to update parameters in one policy network (denoted as θ), and the gradient can be derived as follows:

3.2.4 Training Algorithm

3.3 Discussions

3.3.1 Justification of Dual GATs

(1)
[外链图片转存失败,源站可能有防盗在这里插入!链机制,建描述]议将图片上https://传(imblog.csdmg.-n/96ed9d9actSb2e264f13a4062056537781dd.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBAaGFueGluXw==,size_20,color_FFFFFF,t_70,g_se,x_16,#pic_center)ihttps://img-blog.csdnimg.cn/96ed9d9a2e264f13a4062056537781dd.png?text_Q1NETiBAaGFueGluXw==,size_20,color_FFFFFF,t_70,g_se,x_16,width=")]
(2) for the recommendation of candidate item $i^{+}$ to targeted user $u^{+}$
item $i^{+}$ is similar to item $i_1$
item $i^{+}$ is similar to item $i_2$
here, we assume that user $u^{+}$ has only clicked on $i_i$ and $i_2$, and users $u_1$ to $u_4$ are $u^{+}$'s friends.

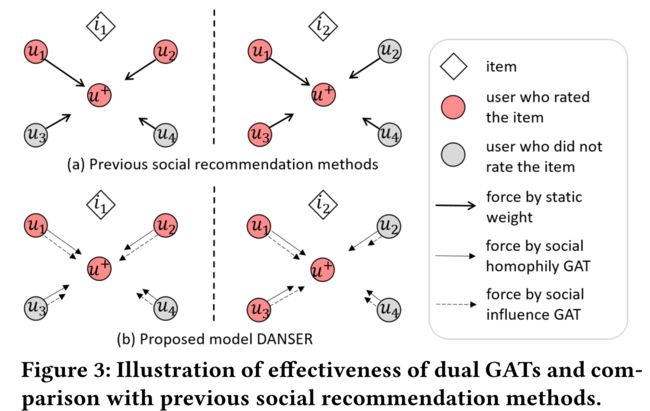
Previous works for social recommendation consider static effect of friends in an average manner.
static weights cannot discriminate between the influence of user u2 and u3 when it comes to item $i^{+}$ even if it is known that it is similar to $i_1$ or $i_2$

4 Experiments

4.1 Experiment Setup

4.1.1 Data Sets

(i) Epinions

Epinions is a consumer review websites, where users can rate some items and add other users in their trust lists.
where items are rated from 1 to 5 (explicit feedback)

(ii) WeChat Top Story

   We also deploy our model on a real-world article recommender system, WeChat Top Story. This dataset is constructed by user-article clicking records on this platform. Different from Epinions, this dataset only contains implicit feedback
   Since the positive samples and negative samples are fairly unbalanced in this dataset, we uniformly sample the negative ones such that the numbers of positive and negative samples are the same for one user.

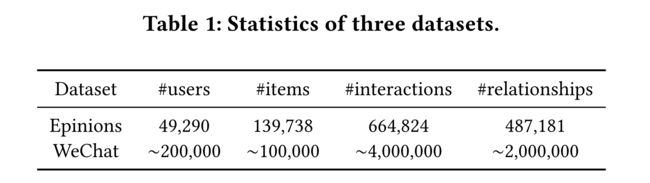
4.1.2 Implementation Details

(一)前人的模型/方法----没用到社交关系的

SVD++

is a basic model-based recommendation method which use both user-specific and item-based user embedding to represent user’s preferences.

DELF

is a state-of-the-art CF method which proposes dual embedding for users and items, and adopts deep neural networks to capture complex non-linear information.

(二)前人的模型/方法----利用了社交关系的(Social Recommendation)

TrustPro

is a trust propagation method, using rating of friends to deduce rating of targeted user.

TrustMF

as one matrix factorization method, optimizes user embedding to retrieve the trust matrix

TrustSVD

is another matrix factorization-based method, incorporating friends’ embedding vectors into targeted user’s predicted rating

NSCR

as a strong baseline for social recommendation, adopts deep neural networks to learn latent representations of users and items, and leverages graph regularization to constrain the embedding of adjacent users to be similar.

SREPS

is another strong baseline, using a network embedding approach to encode social network

4.1.4 Evaluation Protocol

Since two datasets possess different feedbacks, we consider different metrics for them.
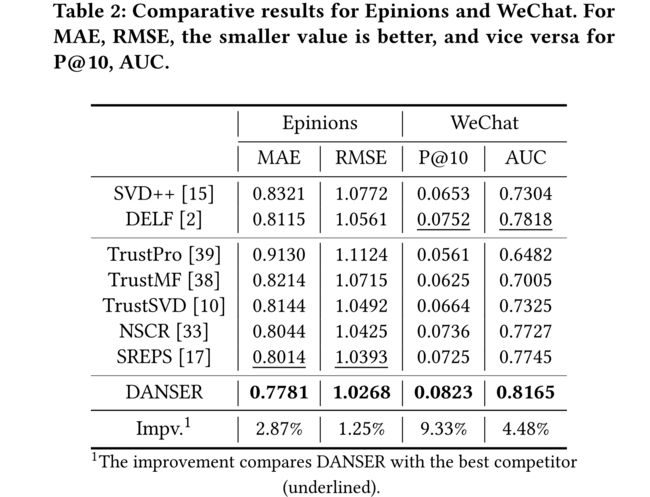
(i) For Epinions with explicit feedback, we use MAE and RMSE, which are widely adopted by other works, as evaluation metrics.
(ii) For WeChat with implicit feedback, we use Precision@k (short as P@k) and AUC, two universally acknowledged metrics for 0-1 classification, to evaluate the performance

4.2 Comparative Results:RQ1

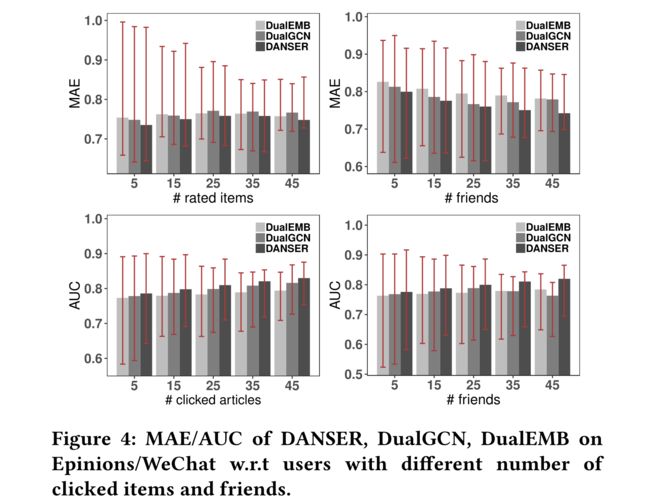
4.3 Ablation Study: RQ2

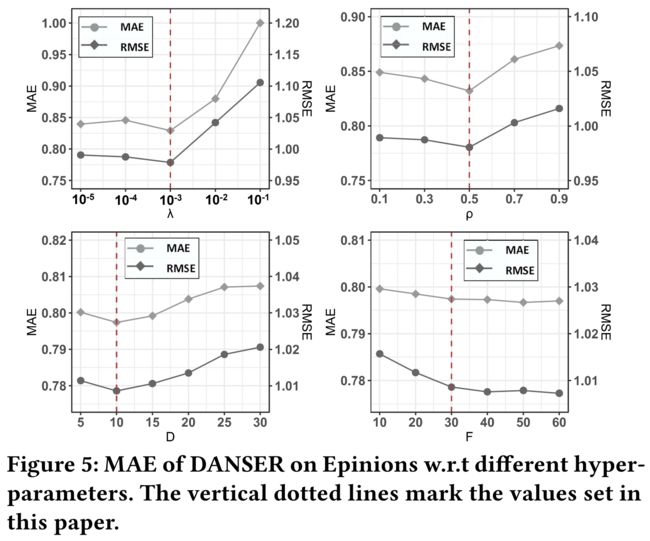
4.4 Parameter Sensitivity: RQ3

hyper-parameters including
regularization parameter $\lambda$
dropout rate $\rho$
embedding dimension $D$
sample size $F$
(The other hyper-parameters have little impact on model performance, so we skip discussions on them for space limit.)

4.5 Case Study: RQ4

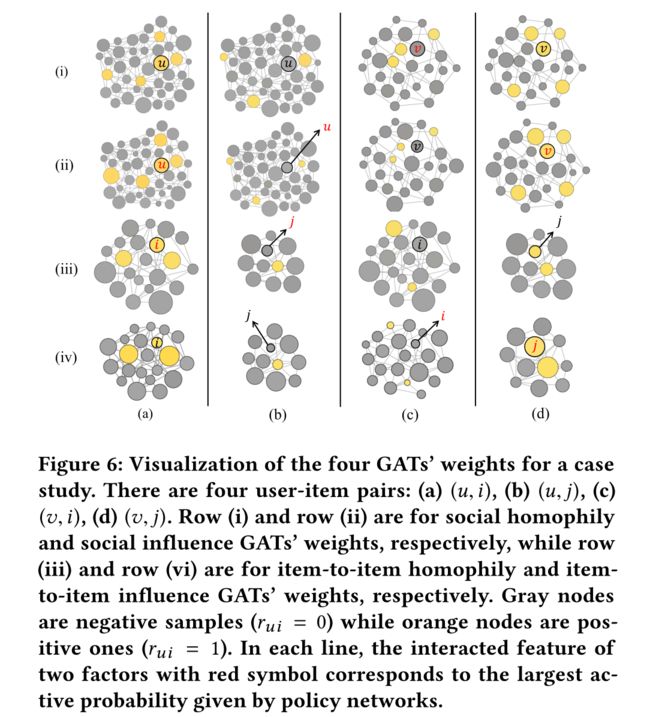
5 Related Works

Social Recommendation

存在的不足

i) they assume neighbors’ influences to be equally important or statically constrained,
ii) they ignore the social effects from related items,
iii) modeling of social effects lacks interpretability

Graph Convolution/Attention Network

Dual Mechanism

6 Conclusion