【OPenGL】OPenGL 画图板-- 中点算法画圆

　　为了能以任意点为圆心画圆，我们可以把圆心先设为视点（相当于于将其平移到坐标原点），然后通过中点法扫描转换后，再恢复原来的视点（相当于将圆心平移回原来的位置）。

      圆心位于原点的圆有四条对称轴x=0,y=0,x=y和x=-y,从而圆上一点(x,y),可得到其关于四条对称轴的七个对称点，这称为八对称性，下面的函数就用来显示(x,y)及其七个对称点.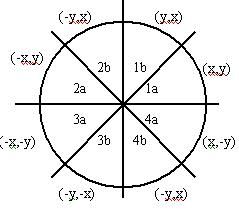

void CirclePoints(int x,int y,long color,CDC *pDC)

{

           //第1象限

           pDC->SetPixel(x,y,color);

           pDC->SetPixel(y,x,color);

           //第2象限

           pDC->SetPixel(-x,y,color);

           pDC->SetPixel(-y,x,color);

           //第3象限

           pDC->SetPixel(-y,-x,color);

           pDC->SetPixel(-x,-y,color);

           //第4象限

           pDC->SetPixel(x,-y,color);

           pDC->SetPixel(y,-x,color);

}

中点画圆算法就是每部单位间隔取样并且计算离圆最近的位置。在继续之前，我这里补充一个关于圆对称性的知识点，通过在圆中计算考虑使用对称性计算开销可以减小到原来的1/8。对称性质原理：

 

（1）圆是满足x轴对称的，这样只需要计算原来的1/2点的位置；

（2）圆是满足y轴对称的，这样只需要计算原来的1/2点的位置；

（3）圆是满足y = x or y = -x轴对称的，这样只需要计算原来的1/2点的位置；

通过上面三个性质分析得知，对于元的计算只需要分析其中1/8的点即可。

例如：分析出来目标点(x,y)必然存在(x,-y),(-x,y),(-x,-y),(y,x),(y,-x),(-y,x),(-y,-x)的另外7个点。

关于中心画圆算法，通过计算x = 0到 x = y的1/8圆的范围，然后通过对称原理得到其他7/8个点的信息。

这里和Bresenham算法有很多相似之处，同样有一个决定下一个位置的关键值P来做权衡处理。

在中点画圆算法中，通过平移的方法将假设圆心在坐标原点，然后计算，最后再平移到真实原心位置。

 

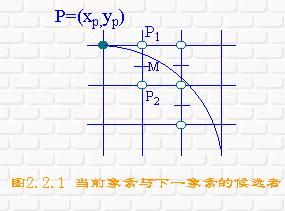
如果我们构造函数 F(x,y)=x2+y2-R2，则对于圆上的点有F(x,y)=0，对于圆外的点有F(x,y)>0，对于圆内的点F(x,y)<0 。与中点画线法一样，构造判别式：

d=F(M)=F(xp+1,yp-0.5)=(xp+1)2+(yp-0.5)2-R2

若 d<0，则应取P1为下一象素，而且再下一象素的判别式为：

d=F(xp+2,yp-0.5)=(xp+2)2+(yp-0.5)2-R2=d+2xp+3

若d≥0，则应取P2为下一象素，而且下一象素的判别式为

d=F(xp+2,yp-1.5)=(xp+2)2+(yp-1.5)2-R2=d+2(xp-yp)+5

我们这里讨论的第一个象素是（0,R），判别式d的初始值为：

d0=F(1,R-0.5)=1.25-R

 

中点画圆算法内容：

1，输入圆心位置和圆的半径，得到圆周上的第一个点Point1;

（假设起始点为坐标原点，后面将通过坐标平移来处理非圆心在圆点）

2，计算决策关键参数的初始值，P = 5/4 - r;

3，在每个Xn的位置，从n = 0开始,更具决策值P来判断：

    如果P<0,下一个点的位置为(Xn+1,Yn);

       并且执行P = P + 2*x+3;

    如果P>=0,下一个点的位置为(Xn+1,Yn-1);

       并且执行P = P + 2.0*(x-y)+5;

4，通过对称原理计算其他7个对称相关点；

5，移动坐标到圆心点(x1,y1)

      X = X + x1;

      Y = Y + y1;

6，如果X<Y重复执行3到5的步骤，否则结束该算法

程序如下：

void Circle::Draw(CDC *pDC)

{//中点算法画圆

    int x,y;

    double p;

    pDC->SetViewportOrg(pMid);

    x=0;

    y=radis;

    p=1.25-radis;

    while(x<=y+1)

    {

        CirclePoints(x,y,m_lPenColor,pDC);

        x++;

        if(p>=0)

        {

            y--;

            p+=2.0*(x-y)+5;

        }

        else

            p+=2*x+3;

    }

    pDC->SetViewportOrg(0,0);

}

源代码下载

原文地址：http://www.cnblogs.com/phinecos/archive/2007/07/28/834407.html