ALNS4VRPTWTF
文章概述
文章研究了城市物流背景下带有第三方转运设施的车辆路径问题。与经典的车辆路径问题不同,这些问题提供了将客户需求交付给第三方转运设施(如城市集散中心)的选择,并收取一定的费用。为了解决这些挑战,该研究提出了一种自适应大邻域搜索(ALNS),其中嵌入了一个随机变量邻域下降作为局部搜索组件,并使用集合划分问题来解决路由重组。
这篇论文介绍并研究了车辆路径问题与转运设施(VRPTF)的两个新问题变体:带有时间窗口和转运设施的车辆路径问题(VRPTWTF)以及带有时间窗口和转运设施的车队规模和混合车辆路径问题(FSMTWTF)。这些变体考虑了与位置有关的时间窗口和异构车队。所提出的方法在现有文献中的基准实例和新创建的实例上进行了测试,显示出有希望的结果,并改进了现有算法。还提出了一个真实世界的研究,以了解转运费用、订单大小和异构车队对转运决策的影响。
研究背景
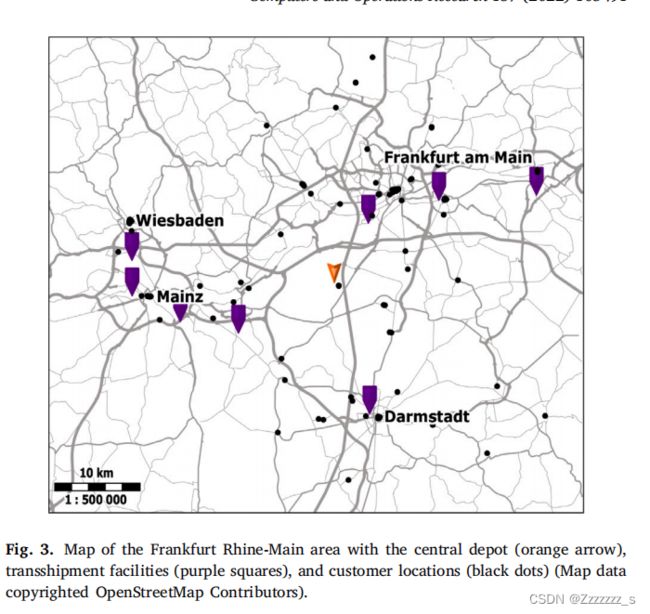
本文的研究背景集中在城市物流领域的车辆路径问题,特别是涉及第三方转运设施的问题。城市物流和最后一公里配送面临诸多挑战,如公众对可持续性的日益关注、城市通行限制和不断增长的配送量。为应对这些挑战,物流服务提供商通常采用在转运设施(如城市集结中心,UCCs)集中货物的方式来提高城市货运效率。城市集结中心定义为靠近城市区域的物流转运设施,可跨公司整合城市货运。尽管有关UCCs的研究众多,且多个城市已实施了UCCs,但很少有研究将个别货件是否外包给第三方转运设施(如UCCs)的决策纳入车辆路径问题中。
问题介绍
文中提到的“带时间窗口和转运设施的车辆路径问题”(VRPTWTF)是一种车辆路径问题(VRP)的变体。在传统的车辆路径问题中,车辆从一个集散中心出发,直接将货物配送到各个客户处。然而,VRPTWTF引入了两个重要的额外特征:时间窗口和转运设施。
-
时间窗口(Time Windows):这指的是每个客户地点可接收货物的特定时间范围。车辆必须在这个时间窗口内到达客户地点,以完成货物交付。时间窗口对路线规划构成了额外的约束,因为它限制了车辆到达各地点的可能时间。
-
转运设施(Transshipment Facilities):在VRPTWTF中,除了直接向客户配送之外,还可以选择将货物先运送到第三方的转运设施,例如城市集结中心(UCCs)。在这些转运设施中,货物可以进行重新整合或中转,之后再由不同的车辆或方式最终配送到客户手中。这种方法特别适用于城市物流,可以帮助缓解城市交通压力、减少碳排放,并提高配送效率。
VRPTWTF的核心挑战在于如何优化车辆路线和货物分配,以在满足时间窗口约束的同时,充分利用转运设施的优势。这包括决定哪些货物应该直接送达客户,哪些应该通过转运设施,以及如何安排车辆路线,使得总成本最低,效率最高。
方法介绍
这篇论文详细介绍了自适应大邻域搜索(ALNS)的方法论,这是一种用于解决车辆路径问题的元启发式方法,其特点是通过移除和插入程序执行大规模移动。该算法涉及初始化参数,创建初始解决方案,然后通过移除和插入程序迭代地破坏和修复解决方案。还嵌入了局部搜索过程以进一步改进解决方案。
搜索空间和目标函数的设计考虑了在搜索过程中关于时间窗约束的不可行解。这是通过使用“时间松弛方案”来实现的,该方案允许车辆“时间倒流”以满足时间窗约束,而这种时间扭曲会用于对目标函数进行惩罚。自适应惩罚参数会根据现有解的可行性进行调整。
算法中的移除程序包括各种启发式方法,比如随机移除、路径移除、最差移除、历史知识节点移除、肖移除、集群移除、与距离相关的移除、与时间相关的移除以及相邻字符串移除。每个程序都有特定的策略来选择从当前解决方案中移除哪些客户请求。
The removal procedures in the adaptive large neighborhood search (ALNS) algorithm, as detailed in the paper, are designed to selectively remove customer requests from the current solution. These procedures play a crucial role in the algorithm’s iterative process of destroying and repairing solutions to find an optimal route. Each removal procedure has its unique strategy and criteria for selecting which customer requests to remove. Here’s a summary of each:
-
Random Removal: This heuristic randomly removes customer requests from a given solution using a uniform probability distribution.
-
Route Removal: In this heuristic, a random route is selected, and up to a certain number of customer requests from the route are randomly removed until the desired number of customers is reached.
-
Worst Removal: Introduced by Ropke and Pisinger (2006a), this heuristic removes customer requests that contribute significantly to the objective function’s cost. It calculates the savings of removing each customer request, sorting them in descending order, and then removing them in a controlled manner.
-
Historical Knowledge Node Removal: This heuristic utilizes historical data, removing customer requests with the highest difference between their current costs and their historically lowest costs.
-
Shaw Removal: Also known as related removal, this method defines the similarity between two customer requests based on several characteristics, including demand difference, distance, time window difference, and shared transshipment facilities. Customer requests are then removed based on these similarities.
-
Cluster Removal: Developed by Ropke and Pisinger (2006b), this method aims to remove an entire cluster of customer requests. It involves partitioning the customer requests in a route into clusters and then removing one of these clusters.
-
Distance-Related Removal: Also known as radial removal, this heuristic removes customer requests that are geographically close to each other.
-
Time-Related Removal: This method removes customer requests that are related in terms of the time they are served.
-
Adjacent String Removal: Introduced by Christiaens and Vanden Berghe (2020), this approach removes adjacent strings of customer requests, aiming to be more efficient by potentially eliminating detours in the destroyed route.
Each of these removal procedures is designed to diversify the search process and avoid local optima by creating variations in the solutions for further exploration.
自适应大邻域搜索(ALNS)算法中的移除过程,如论文中所述,旨在有选择地从当前解中移除客户请求。这些过程在算法的迭代过程中破坏和修复解以找到最优路线起着关键作用。每个移除过程都有其独特的策略和标准来选择要移除的客户请求。以下是每个策略的概述:
-
随机移除:此启发式使用均匀概率分布从给定解中随机移除客户请求。
-
路线移除:在此启发式中,随机选择一个路线,并从该路线中随机移除一定数量的客户请求,直到达到所需的客户数量。
-
最差移除:由Ropke和Pisinger(2006a)引入,此启发式移除对目标函数成本产生显著影响的客户服务请求。它计算移除每个客户服务请求的节省,按降序排序,然后以受控的方式移除它们。
-
历史知识节点移除:此启发式利用历史数据,移除具有当前成本与历史最低成本之间最高差异的客户请求。
-
Shaw移除:也称为相关移除,此方法根据几个特征定义两个客户服务请求之间的相似性,包括需求差异、距离、时间窗口差异和共享运输设施。然后根据这些相似性移除客户服务请求。
-
集群移除:由Ropke和Pisinger(2006b)开发,此方法旨在移除整个客户服务请求集群。它涉及将路线上的客户服务请求划分为集群,然后移除其中一个集群。
-
距离相关移除:也称为径向移除,此启发式移除地理位置相近的客户请求。
-
时间相关移除:该方法移除与提供服务的时间相关的客户服务请求。
-
相邻字符串移除:由Christiaens和Vanden Berghe(2020)引入,此方法移除相邻的客户请求字符串,旨在通过可能消除被破坏路线上的绕路来提高效率。
每个移除过程都设计为多样化搜索过程,并通过在解决方案中创建变化以避免局部最优解,从而进一步探索。
插入程序用于将已删除的客户请求重新整
合到解决方案中。这些程序包括随机顺序最佳插入、需求顺序最佳插入、最远优先最佳插入和最近优先最佳插入。这些程序考虑需求、到仓库的距离和其他标准来确定最佳插入位置。
本地搜索过程通过将ALNS方法与随机变邻域下降(RVND)相结合来加强搜索。这涉及选择邻域并在解决方案中寻找改进。该算法还使用各种路由间和路由内邻域来实现更好的局部最优解。
研究结论与讨论
最后,本文讨论了一个由混合整数规划(MIP)求解的集合分割问题(SP)模型。该模型有助于在确保每个客户请求在解决方案中仅包含一次的同时,最小化路线成本之和。该模型针对车队规模和混合问题变体进行了调整。