【LeetCode.53】 最大子序和——以及变种 返回开始结束索引
题目描述
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例:
输入: [-2,1,-3,4,-1,2,1,-5,4],
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
解法——动态规划
很标准的动态规划:
- 记
dp[i]代表范围为[0,i]闭区间的子数组的最大子序和,注意子序列至少包含i元素,即子序列的区间为[i,i]。所以,准确的说,dp[i]代表范围为[0,i]闭区间内,以i元素作为末尾元素的子数组的最大子序和。 - 此题满足 最优子结构和无后效性 两大动态规划的要求。所以,递推公式为
dp[i+1] = max(nums[i+1], dp[i]+nums[i+1]),因为最大子序列,要么只有末尾元素,要么末尾元素再算上dp[i]的最大子序列。
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
maxNum = nums[0]
for i in range(1,len(nums)):
if nums[i-1] > 0:
nums[i] += nums[i-1]
maxNum = max(maxNum,nums[i])
return maxNum
- 不用新建一个dp数组了,直接在nums数组上覆盖就好,因为无后效性,当前元素遍历后,就可以覆盖为
dp[i]的值。 dp[0]的值,初始时,就是确定的,因为只有一个元素的数组,它的唯一的子序列就是它自己。- 从递推公式
dp[i+1] = max(nums[i+1], dp[i]+nums[i+1])可以看出,其实关键在于上一次递推结果是否大于0,如果大于0,那么当前递推结果就得加上 上一次递推结果。 - maxNum在遍历过程,保存最大的那个递归结果。
变种 返回开始结束索引
现在改一下题目,要求返回 最大子序列 的开始索引和结束索引。那么代码应该如下:
class Solution:
def maxSubArray(self, nums):
maxNum = nums[0]
start = end = 0
finalStart = finalEnd = 0
for i in range(1,len(nums)):
if nums[i-1] > 0:
nums[i] += nums[i-1]
end = i
else:
start = end = i
if nums[i] > maxNum:
finalStart = start
finalEnd = end
maxNum = max(maxNum,nums[i])
return [finalStart, finalEnd]
- start、end代表当前第
i次遍历后,[0,i]闭区间内,以i元素作为末尾元素的子数组的最大子序列的开始结束索引。 - start、end的更新策略:
- 如果上一次递推结果大于0,那么只往后移动end,因为最大子序列只是末尾多了一个元素。
- 如果上一次递推结果小于0,那么start、end都应该更新为i,因为当前的最大子序列,只有i元素了。
- 如果上一次递推结果等于0,这里程序将它归为小于0的处理。其实还是有区别的,如上代码,测试用例为
[4,-4,1,6],那么将返回[2, 3];如果改成if nums[i-1] >= 0:,那么将返回[0, 3]。区别就是,会不会将和为0的子序列算入其中。所以,再给此变种题目加上,是否算上和为0的子序列,就可以确定 递推结果等于0时的处理。
- finalStart、finalEnd在遍历过程,保存最大子序列的开始结束索引。
if nums[i] > maxNum:分支处理和maxNum = max(maxNum,nums[i])异曲同工,后者也是只有当nums[i] > maxNum才会更新maxNum。
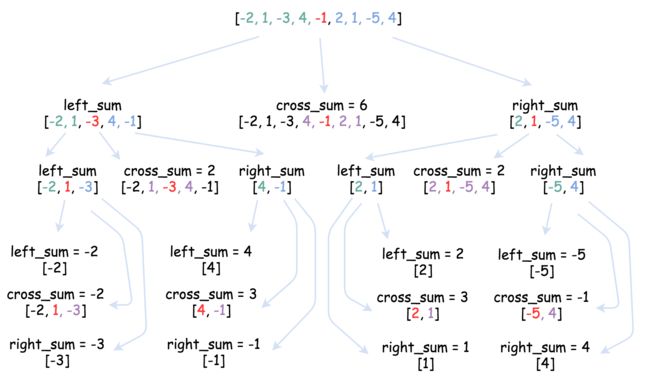
解法——分治法(使用递归)
class Solution:
def cross_sum(self, nums, left, right, p):
if left == right:
return nums[left]
left_subsum = float('-inf')
curr_sum = 0
for i in range(p, left - 1, -1):
curr_sum += nums[i]
left_subsum = max(left_subsum, curr_sum)
right_subsum = float('-inf')
curr_sum = 0
for i in range(p + 1, right + 1):
curr_sum += nums[i]
right_subsum = max(right_subsum, curr_sum)
return left_subsum + right_subsum
def helper(self, nums, left, right):
if left == right: #区间内只有一个元素,无法再划分。子序列只能是区间本身,那么返回这个元素
return nums[left]
#执行到这里,说明现在是递归的过程。把该次调用的区间分为两部分。
#left_sum和right_sum需要调用本身(递归)获得,cross_sum需要调用另一函数
p = (left + right) // 2
left_sum = self.helper(nums, left, p) #得到[left,p]区间内的最大子序和
right_sum = self.helper(nums, p + 1, right) #得到[p+1,right]区间内的最大子序和
cross_sum = self.cross_sum(nums, left, right, p) #得到必包含[p,p+1]且可左右延伸的可能序列的最大序列和
#上面三者算完,才把[left,right]区间内 所有可能子序列的和都计算了一遍
return max(left_sum, right_sum, cross_sum)
def maxSubArray(self, nums: 'List[int]') -> 'int':
return self.helper(nums, 0, len(nums) - 1)
- 如果把数组分为两部分,那么最大子序列,要么在左边,要么在右边,要么跨越了左右两边(准确的描述,是指至少包含了左半边的最右元素和右半边的最左元素的,且可以向左右延伸的子序列)。
- 其实本算法,主要全靠 寻找跨越了左右两边的子序列的函数cross_sum,因为它计算大部分可能子序列的和。
- 注意cross_sum开始有个特殊判断
if left == right:,防止这两个索引一样,但实际上,传入这个函数的left和right应该至少差1,因为就算二者相等,也会在helper函数的开头的特殊判断里被检测到。实际上,你把cross_sum开始的特殊判断if left == right:,再提交解答,也能通过。(不过,可能这就是算法题的严谨吧,哈哈哈哈) - 为了让算法过程更加清晰,我加上打印:
class Solution:
def cross_sum(self, nums, left, right, p):
if left == right:
return nums[left]
left_subsum = float('-inf')
curr_sum = 0
for i in range(p, left - 1, -1):
curr_sum += nums[i]
left_subsum = max(left_subsum, curr_sum)
right_subsum = float('-inf')
curr_sum = 0
for i in range(p + 1, right + 1):
curr_sum += nums[i]
right_subsum = max(right_subsum, curr_sum)
return left_subsum + right_subsum
def helper(self, nums, left, right):
if left == right:
print(left,right,nums[left])
return nums[left]
p = (left + right) // 2
left_sum = self.helper(nums, left, p)
right_sum = self.helper(nums, p + 1, right)
cross_sum = self.cross_sum(nums, left, right, p)
temp = max(left_sum, right_sum, cross_sum)
print('[%d-%d] left_sum is %d, [%d-%d] right_sum is %d, cross_sum is %d. So [%d,%d] max is %d'%(
left,p,left_sum,p+1,right,right_sum,cross_sum,left,right,temp))
return max(left_sum, right_sum, cross_sum)
def maxSubArray(self, nums: 'List[int]') -> 'int':
return self.helper(nums, 0, len(nums) - 1)
so = Solution()
li = [7,-8,-9,3,-1,2,-1,7,1]
print(so.maxSubArray(li))#输出11
0 0 7
1 1 -8
[0-0] left_sum is 7, [1-1] right_sum is -8, cross_sum is -1. So [0,1] max is 7
2 2 -9
[0-1] left_sum is 7, [2-2] right_sum is -9, cross_sum is -10. So [0,2] max is 7
3 3 3
4 4 -1
[3-3] left_sum is 3, [4-4] right_sum is -1, cross_sum is 2. So [3,4] max is 3
[0-2] left_sum is 7, [3-4] right_sum is 3, cross_sum is -6. So [0,4] max is 7
5 5 2
6 6 -1
[5-5] left_sum is 2, [6-6] right_sum is -1, cross_sum is 1. So [5,6] max is 2
7 7 7
8 8 1
[7-7] left_sum is 7, [8-8] right_sum is 1, cross_sum is 8. So [7,8] max is 8
[5-6] left_sum is 2, [7-8] right_sum is 8, cross_sum is 9. So [5,8] max is 9
[0-4] left_sum is 7, [5-8] right_sum is 9, cross_sum is 11. So [0,8] max is 11
从打印第三行可以看到,递归调用第一次返回到递归树的叶子节点的上一层。[0-0]区间只有一个元素,所以它的最大子序列为它本身。[1-1]同理。cross_sum至少包含[0-1]区间,但已经无法左右延伸了,所以就是0元素加上1元素。