不到十个例题带你拿下c++双指针算法（leetcode）

移动零问题

https://leetcode.cn/problems/move-zeroes/submissions/

1.题目解析

必须在原数组进行修改，不可以新建一个数组

非零元素相对顺序不变

2.算法原理

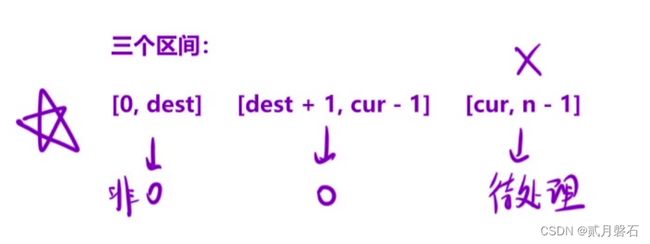
【数组划分】【数组分块】

这一类题会给我们一个数组，让我们划分区间，比如说这题，最后会划分为两个区间，前一段是非零元素，后一段是零，一般我们只要看到这样的特性，脑海里就应该想到用双指针算法来解决（利用数组下标充当指针）

定义两个指针：

两个指针的作用：

cur ：从左往后扫描数组，遍历数组。

dest : 已处理的区间内，非零元素的最后一个位置

如何做到：

cur从前往后遍历的过程中：

1.遇到0元素：cur++；

2.遇到非零元素：

交换

相关知识：快速排序

双指针的思想其实就是快排的核心思想

class Solution {
public:
    void moveZeroes(vector& nums) {
       for(int cur=0,dest=-1;cur

 

复写零问题

https://leetcode.cn/problems/duplicate-zeros/

1.题目解析

长度固定：不能越界

在原始数组进行操作

2.算法原理：

解法：双指针算法 先根据异地操作，然后优化成双指针下的“就地操作”

根据异地操作，得出先模拟一遍复写的操作，然后从后向前进行覆盖，从前往后会发生覆盖多的值。

总结：

1.先找到最后一个复写的数

用双指针模拟一遍 cur=0，dest=-1；

先判断cur位置的值，决定dest向后移动几步，判断dest是否已经到了最后的位置，cur++；

2.从后向前进行操作

特例：数组越界

所以要加上一个步骤：处理越界

3.解题代码：

class Solution {
public:
    void duplicateZeros(vector& arr) {
        int cur=0,dest=-1,n=arr.size();
        //先模拟
        while(cur=n-1) break;
            cur++;
        }
        //判断边界
        if(dest==n)
        {
            arr[n-1]=0;
            dest-=2;
            cur--;
        }
        //从后向前
        while(cur>=0)
        {
            if(arr[cur]==0)
            {
                arr[dest--]=0;
                arr[dest--]=0;
                cur--;
            }
            else arr[dest--]=arr[cur--];
        }
    }
};

 

快乐数问题

https://leetcode.cn/problems/happy-number/

1.题目解析

一直替换

分为两种情况：

变成一

无限循环

两种情况

2.算法原理

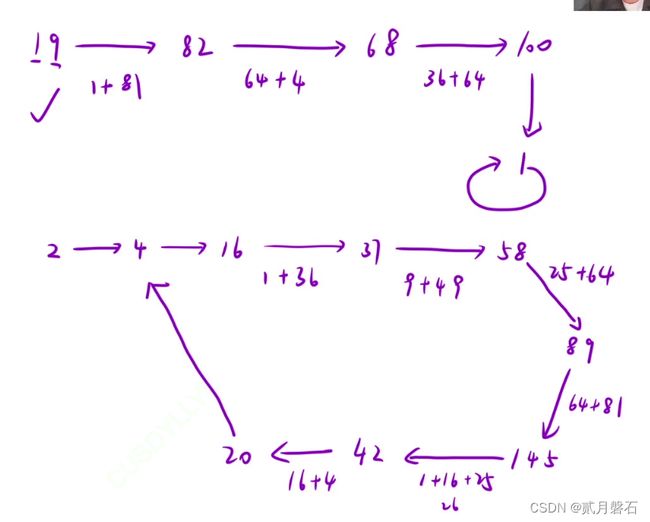
有没有发现，一直平方到最后，一定会成环

解法：快慢双指针

1.定义快慢双指针

2.慢指针每次向后移动一步，快指针每次走两步

3.判断相遇的时候的值即可

双指针只是一种思想，不需要一定定义双指针，在这个题中快指针就是平方两次，慢指针平方一次

为什么会一定会重复

证明方法：

鸽巢原理（抽屉原理）：

n个巢穴 n+1个鸽子-->至少有一个巢穴里面的鸽子数量大于1

3.解题代码

class Solution {
public:
    int Sum(int n)
    {
        int sum=0;
        while(n)
        {
            int g=n%10;
            sum+=g*g;
            n/=10;
        }
        return sum;
    }
    bool isHappy(int n) {
        int slow=n,fast=Sum(n);
        while(slow!=fast)
        {
            slow=Sum(slow);
            fast=Sum(Sum(fast));
        }
        return slow==1;
    }
};

盛水最多的容器

https://leetcode.cn/problems/container-with-most-water/

1.题目解析

只能水平放置，也就是找最大的矩形

2.算法原理

解法一：暴力枚举：双重循环

优点：想法简单

缺点：时间复杂度过高

解法二：头尾双指针：

v=h*w

宽度一直在减小，而高度有两种情况，变大或变小，在宽度一直在变小的情况下，我们高度必须选择更高的

3.解题代码

class Solution {
public:
    int maxArea(vector& height) {
        int left=0,right=height.size()-1;
        int v=-1;
        while(leftheight[right])  right--;
            else                            left++;
        }
        return v;
    }
};

和为s的两个数字问题

1.题目解析

有序数组

随意输出一对

2.算法原理

解法一：暴力枚举 双重循环 n^2复杂度

解法二：利用单调性，使用双指针算法解决问题

首尾相加

判断数值，如果大于目标值，right--反之left++，因为数组是有序的

3.解题代码

vector twosum(vector &nums,int t)
{
  int left =0,right=nums.size()-1;
  while(leftt) right--;
    else if(sum

有效三角形个数

https://leetcode.cn/problems/valid-triangle-number/

1.题目解析

相同的不算一个

2.讲解算法原理

补充数学知识：给我们三个数，判断是否能构成三角形

我们仅需要一个公式，就能判断是否能构成三角形：

如果我们已经知道三个数的大小顺序，只需要a+b>c（c是最大的数）

优化：先对整个数组排序

解法一：暴力枚举

for(i=0;i

for(j=i+1;j

解法二：利用单调性，使用双指针算法来解决问题

①先固定最大的数

②在最大的数的左区间里，使用双指针算法，快速统计

3.解题代码

class Solution {
public:
    int triangleNumber(vector& nums) 
    {
        int n=nums.size();
        int ret=0;
        sort(nums.begin(),nums.end());
        for(int i=n-1;i>=2;i--)
        {
            int left=0,right=i-1;
            while(leftnums[i])
                {
                 ret+=right-left;
                 right--;
                }
                else
                {
                left++;
                }
            }
        }
        return ret;
    }
};

三数之和问题

https://leetcode.cn/problems/3sum/

1.题目解析

三个数的下标不同

答案不可重复（去重）

有可能没有答案

2.算法原理

解法一：先排序+暴力枚举+利用set去重o(n^3)

解法二：排序+双指针：

找到右边区间两数之和为左边数字的相反即可

1.排序

2.固定一个数a

3.在该数后边的区间，利用双指针的算法，快速找到和为-a的两个数

处理细节问题：

1.去重：

找到一种结果之后，left和right指针要跳过重复元素。

当使用完一次双指针算法之后，i也要跳过重复元素（避免越界）

2.不漏：

找到一种结果后，不要“停”，缩小区间，继续寻找

3。解题代码

class Solution {
public:
    vector> threeSum(vector& nums) {
        sort(nums.begin(),nums.end());
        vector> ret;
        int n=nums.size();
        for(int i=0;i0) break;
            int left=i+1,right=n-1,t=-nums[i];
            while(leftt) right--;
                else
                {
                    ret.push_back({nums[i],nums[left],nums[right]});
                    left++,right--;
                    while(left

四数之和

https://leetcode.cn/problems/4sum/

1.题目解析

三数之和的进阶版本，基本算法原理和三数之和大差不差

2.算法原理

解法一：排序＋暴力枚举

四个循环，绝对超时

解法二：排序＋双指针

1.依次固定一个数i

2.在i后面的区间内，利用三数之和找到三个数，让他们三个的和等于target-i；

{

1.依次固定一个j

2.在j后边的区间里，利用“双指针找到两个数，使得这两个数之和等于target-i-j”

}

处理细节问题：

不重，不漏

3.解题代码：

class Solution {
public:
    vector> fourSum(vector& nums, int target) {
              vector> ret;
            //1.排序
            sort(nums.begin(),nums.end());
            //2.利用双指针解决问题
            int n=nums.size();
            for(int i=0;iaim) right--;
                        else
                        {
                            ret.push_back({nums[i],nums[j],nums[left++],nums[right--]});
                        //去重1
                        while(left

觉得有帮助的惯用老爷麻烦点点关注！！！