RISC Zero的手撕STARK

1. 引言

RISC Zero虚拟机内的任意代码在执行时，该执行的每个step都记录在Execution Trace中。

以2个用户指定的输入，Fibonacci sequence模97的4步计算为例。本文将介绍：

• 介绍RISC Zero Execution Trace的各列。
• 展示了如何在不泄露任何knowledge的情况下，RISC Zero证明某Execution Trace的有效性，的具体例子。

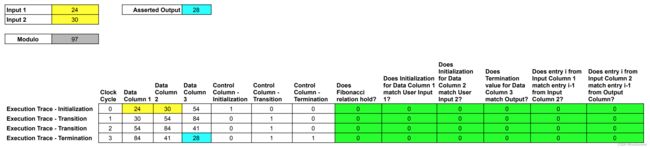
本文所举例子中，其Execution Trace共有6列，其中：

• 前3列的每列分别用于记录，从初始化到结束某寄存器的内部状态。将前3列称为Data Columns。
• 后3列为Control Columns，用于标记初始化和结束节点。

在整个RISC Zero协议中，Data Columns用于维护RISC-V处理器的状态，包括：

• ISA寄存器
• program counter
• 各种微架构细节，如指令解码数据、ALU寄存器等。

等的状态。Control Columns用于处理：

• 系统初始化和关机（shutdown）
• 在执行之前，将初始程序代码加载到内存
• 其它不依赖于程序执行的control signals。

2. Checking the Execution Trace（增加检查规则列）

为展示本例中Execution Trace的有效性，需引入一些rule-checking cells。

在本例中展示了6条规则：（而在整个RISC-V实现中，为验证相应Execution Trace，需检查超过100条规则。）

• 每条规则的检查，表示为2项之积，再模97：
  • 当第一项为0，则该规则成立。
  • 当第二项为0，则表示无需强化该规则。
• 每个rule checking column（见下图绿色所示列），可表示为多输入、单输出的多项式，其输入可为该Execution Trace中各元素的某种组合。称这样的多项式为Rule-Checking Polynomials。

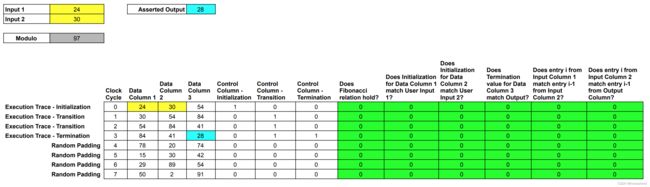
3. Adding Random Padding（增加随机填充行，以实现零知识属性）

在将每列编码为某多项式之前，需在该Execution Trace中附加随机填充行，从而支持零知识协议。这些随机噪声由host system的密码学安全伪随机数生成器 生成。为关闭对随机噪声行的规则检查，可设置这些随机噪声行的Control columns值为0。

4. Interpolating Trace Polynomials（对trace各列插值获得trace polynomials）

此时，暂时先移除不考虑rule-checking列，并将注意力用于将Trace data编码为多项式。类似于任意2点间可画线，任意8个点可确定某degree为7的多项式。已知一组点，构建经过这些点的某多项式的标准技术为Lagrange插值和FFT（Finite Fourier Transforms）。在RISC Zero上下文中，使用NTT（Number Theoretic Transforms）——为有限域版本的FFT。

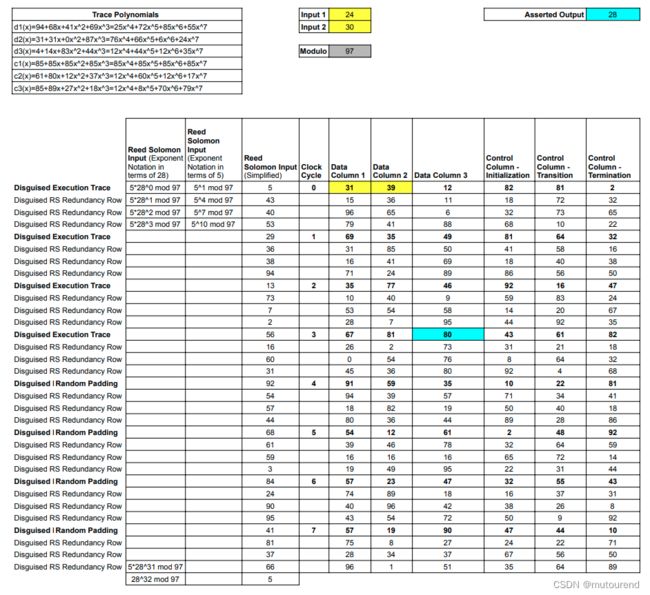
由于本例中使用的是模97，因此，相应多项式的evaluation值和系数均在有限域$F_{97}$中。RISC Zero所采用的多项式编码技术称为Reed-Solomon encoding。

RS codes在数字信号处理世界中无处不在，用于提供冗余，以做错误发现和纠错。Reed-Solomon Codes采用的点格式为$(a^0,x_0),(a^1,x_1),\cdots$。

在本例中，将powers of $28$（因有 $5^3\mathrm{mod}97=28$）当做输入（并将该Execution Trace中的元素作为输出）。RISC Zero使用该技术来将该trace中的每列表示为某Trace Polynomial。如：

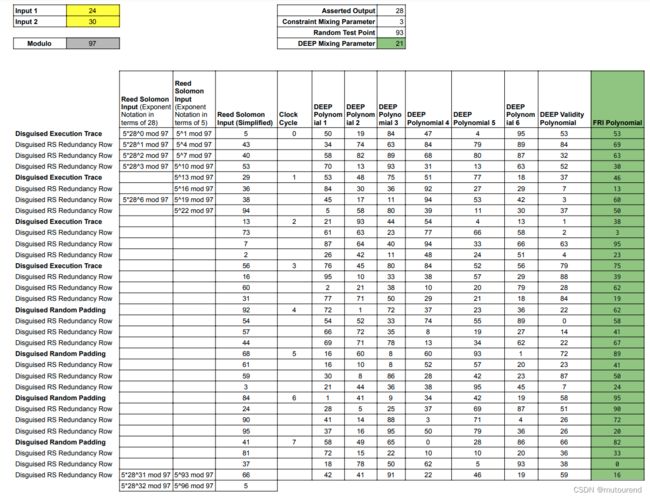
• 1）对Data Column 1的8个元素运行iNTT，使用iNTT(column, modulus)来生成某Trace Polynomial $d_1$，该多项式的evaluation值与这8个元素的值对应。【Data Column 1的这8个元素在下图中以黑色加粗表示，每个元素对应Padded Trace中的一行。】
  • 在Python中，using sympy, intt([24, 30, 54, 84, 78, 15, 29, 50], prime=97)，返回[94, 68, 41, 69, 25, 72, 85, 55]。iNTT的输出值对应为Trace Polynomial的系数，即Trace Polynomial $d_1(x)=94+68x+41x^2+69x^3+25x^4+72x^5+85x^6+55x^7(\mathrm{mod}97)$。
  • $d_1(x)$的关键特性在于，当$z=5^0,5^{12},5^{24},\cdots$时，$d_1(z)$的evaluation值与Data Column 1的8个元素值对应：即$d_1(5^0)=24,d_1(5^{12})=30,d_1(5^{24})=54$等等。【其中$5$为$F_{97}$域的$96$-th root of unity。】
• 2）然后对该Trace Polynomial $d_1$在Expanded Domain进行evaluate，已构建该列的Reed Solomon编码。
  • 若blowup-factor为4，则相应的Reed-Solomon input（即对$d_1(x)$的evaluate点）为：$5^0,5^3,5^6,\cdots$。

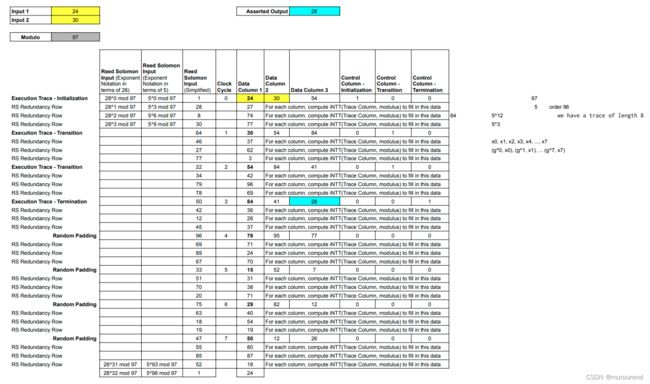
以此类推，对Execution Trace中的其它Data Column和Control Column做类似以上的操作，即本例中，一共有6个Trace Polynomials，每个Trace Polynomial分别在32个点上进行evaluate，以获得Reed-Solomon编码：

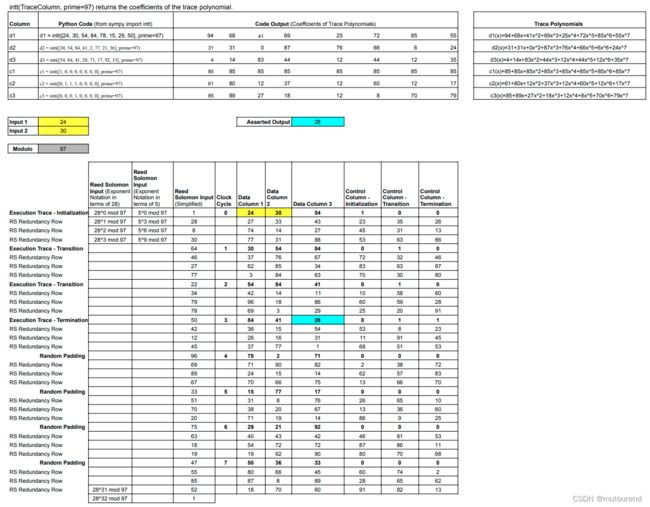
5. Committing Trace Polynomials

接下来，Prover会将Trace Polynomials承诺到a Merkle tree中。为实现零知识属性，Prover会对每个Trace Polynomial，基于“a shifted evaluation domain”来进行evaluate，即在 $x=5^1,5^4,5^7,\cdots ,5^{94}$ 对每个$d_i(x)$进行evaluate。

注意，由于采用的是shifted evaluation domain，下图中Data Column 1、2、3中的黄色和蓝色单元格内的值，将不再与Inputs和Asserted Outputs值匹配了。事实上，在evaluation domain的这种便宜，可掩饰所有Trace Data。仅公开掩饰后的trace信息，且附加的随机padding，足以防止攻击者推断出“掩饰后的trace”与“实际trace”之间的任何关联信息。

6. Introducing Constraint Polynomials

至此，已将Trace Data编码为了Trace Polynomials。

回到原始的Reed-Solomon domain，并将Rule Checking cells加回：

• 对于RS Redundancy Row，不应期待其rule checks会evaluate为0值，因为其与Execution Trace中的数据无直接关系。
• 与Trace Polynomials类似，可将这些rule checks对应的multi-input rule checking polynomials 转换为 single-input polynomials——即称为Constraint Polynomials。
  • 注意，每个Constraint Polynomials，在与实际trace data相关的RS input values点处的evaluation值为0。

【注意下图中为展示原理，采用的是未便宜evaluation domain。】

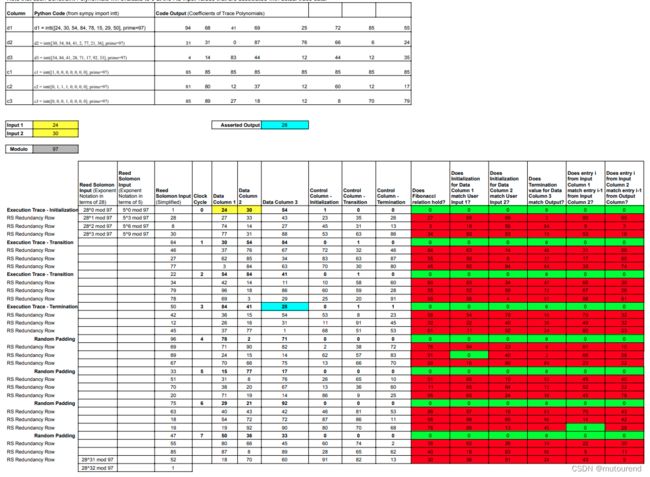
6.1 Mixing Constraint Polynomials

再额外增加一列，用于将多个Constraint Polynomials 混合为单个Constraint Polynomial。

在Prover发送完每个Trace Polynomial的Merkle root之后，Verifier会回复一个Constraint Mixing Parameter——$a$。【下图中，取$a=3$。】

对于$i=0,1,2,3,4,5$，以$c_i$来表示相应的Constraint Polynomials，则利用Verifier提供的约束混合参数$a$，可将多个Constraint Polynomials 混合为单个Constraint Polynomial：
$C(x)=a^0\ast c_0(x)+a^1\ast c_1(x)+\cdots +a^5\ast c_5(x)$。【注意，若每个$c_i$在某个输入$x$处的evaluation值均为0，则在相应输入$x$处，$C$的evaluation值也将为0。】

在本例中，Mixed Constraint Polynomial的degree，等于，Trace Polynomials的degree，因为所包含的Rule-Checking特别简单。实际在更复杂的例子中，将Rule Checking Polynomials和Trace Polynomials组合，可能会生成“High Degree Constraint Polynomials”——此时，需增加额外的步骤：

• 将“High Degree Mixed Constraint Polynomial” 切分为一些“Low Degree Mixed Constraint Polynomials”。

【注意，实际为实现零知识属性，下图展示的是shifted evaluation domain下的各值。】

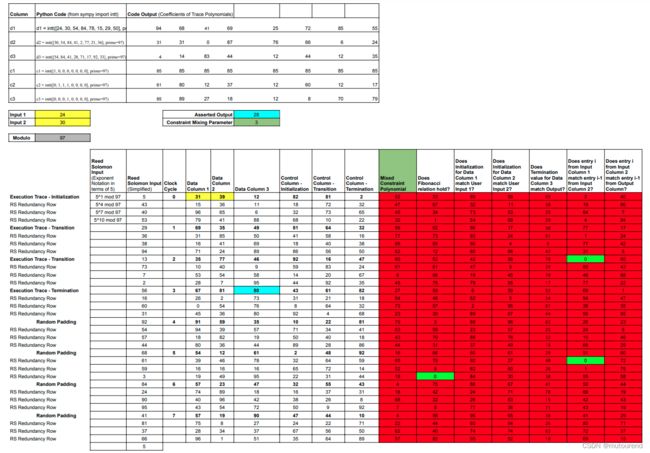
7. RISC Zero STARK核心

Prover构建Validity Polynomial：

• 将Constraint Polynomial 除以 公开已知的Zeros Polynomial，即$V(x)=C(x)/Z(x)$。

在本例中，Zeros Polynomial为$Z(x)=(x-1)\ast (x-64)\ast (x-22)\ast (x-50)\ast (x-96)\ast (x-33)\ast (x-75)\ast (x-47)$。【即对应未偏移evaluation domain，对Execution trace中所取的Reed Solomon input —— $(5^0\mathrm{mod}97,5^{12}\mathrm{mod}97,5^{24}\mathrm{mod}97,\cdots ,5^{84}\mathrm{mod}97)$。】

正常对2个low degree多项式做除法运算时，不一定能获得另一个low degree多项式（更大概率是获得rational function）。但对于诚实的Prover，其不难看出$V(x)$的degree 要比 $C(x)$的degree 低，因为$Z(x)$的根 正好与 $C(x)$的根 对齐。

如下图所示，Prover基于“shifted evaluation domain”来对$V(x)$进行evaluate，并将相应的evaluation值承诺到a Merkle tree中，并将相应的Merkle root发送给Verifier。

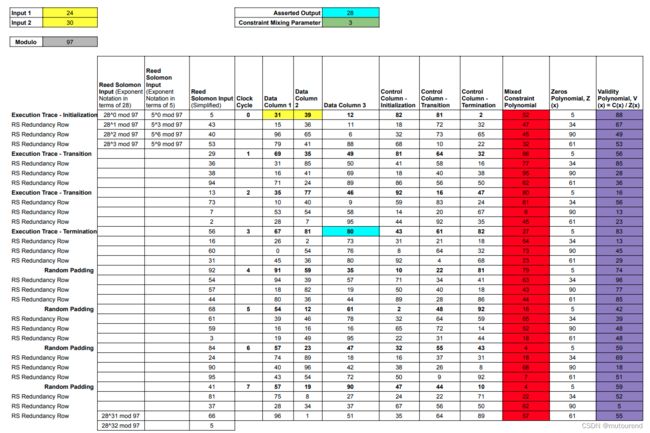
这些多项式的构建，是RISC Zero的Trace Validity Proof的核心概念要点。确认原始Execution Trace有效性 所需的所有信息，均可描述为关于这些多项式的如下assertions：

• 1）对于所有的$x$，有$V(x)=C(x)/Z(x)$。【RISC Zero采用DEEP-ALI协议来证明。】
• 2）Validity Polynomial $V(x)$的degree小于等于7，且每个Trace Polynomials的degree也小于等于7。【使用FRI协议来证明。本文忽略具体细节。】

在原始的STARK协议中，Verifier为验证 “对于所有的$x$，有$V(x)=C(x)/Z(x)$。”，需在一组test points进行测试，该协议的soundness取决于测试的次数。
DEEP-ALI技术，支持以单个测试，来实现high degree soundness。

7.1 Constructing the DEEP Polynomials

使用Trace Polynomials和Validity Polynomial(s) 来构建DEEP Polynomials。

DEEP Polynomials支持Verifier在原始Merkle tree commitments之外 来测试$V(x)=C(x)/Z(x)$，这大大提高了Verifier测试的鲁棒性。

基本流程为：

• 根据Trace Polynomials的承诺值，以及Validity Polynomial的承诺值，Verifier选择随机域元素$z$。【在本例中，取$z=93$。】
• Verifier想要计算Mixed Constraint Polynomial在$z$点的evaluation值$C(z)$。
  • Prover发送$V(z)$和所需的Trace Polynomial相关evaluation值 给Verifier，使得Verifier可计算出$C(z)$。
    如本例中取$z=93$，为让Verifier可计算出$C(93)$，Prover需提供的evaluation值有：
    • $d_1(93),d_2(93),d_3(93),c_1(93),c_2(93),c_3(93)$，以及$d_2(93\ast 5^{-12}),d_3(93\ast 5^{-12})$。这8个值，称为taps of the trace at 93。
      • 其中$5^{-12}$表示指向前一计算step，并支持跨多个clock-cycles的Rule Cchecking。【若$5^{12}$则表示指向后一计算step。】
      • 根据这8个值，以及公开已知的rule-checking函数，Verifier可计算出$C(93)$，进而进一步计算出$V(93)$。
• Prover也会构建DEEP Polynomials，每个DEEP Polynomial插值，并将每个DEEP Polynomial的系数发送给Verifier。
  • 本例中，具体的DEEP Polynomial定义为：【因实际约束规则中对Data Column 2和Data Column 3的前一计算step的值有约束，因此对$d_2,d_3$除取当前点$93$之外，还需取其前一计算step的点$6$。】
    $d_1^{\prime }(x)=(d_1(x)-d_1(93))/(x-93)$
    $d_2^{\prime }(x)=(d_2(x)-dba{r}_2(x))/((x-93)(x-6))$：其中$dba{r}_2(x)$为对 $(6,d_2(6))$ 和 $(93,d_2(93))$的插值多项式。【其中$6,93$均为Non-Merkle Points】
    $d_3^{\prime }(x)=(d_3(x)-dba{r}_3(x))/((x-93)(x-6))$：其中$dba{r}_3(x)$为对 $(6,d_3(6))$ 和 $(93,d_3(93))$的插值多项式。【其中$6,93$均为Non-Merkle Points】
    $c_1^{\prime }(x)=(c_1(x)-c_1(93))/(x-93)$
    $c_2^{\prime }(x)=(c_2(x)-c_2(93))/(x-93)$
    $c_3^{\prime }(x)=(c_3(x)-c_3(93))/(x-93)$
    $V^{\prime }(x)=(V(x)-V(93))/(x-93)$：其中Prover为计算$V(93)$，运行iNTT(ValidityColumn)，然后对其在93进行evaluate。具体的Python代码为：intt([ 88,67,49,53,56,85,28,36,16,56,13,23,83,13,45,29,74,96,77,85,42,39,48,48,59,69,18,51,59,52,5,55], prime=97)，返回的$V$多项式系数为 [96, 83, 47, 58, 36, 60, 96, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]。
  • 若不使用DEEP技术，则Prover将断言$d_1,d_2,d_3,c_1,c_2,c_3$和$V$均为low degree多项式。
  • 若使用DEEP技术，则Prover将断言$d_1^{\prime },d_2^{\prime },d_3^{\prime },c_1^{\prime },c_2^{\prime },c_3^{\prime }$和$V^{\prime }$均为low degree多项式。

7.2 The FRI Polynomial

在使用DEEP Polynomials来检查，Trace Polynomials、Validity Polynomial和Zeros Polynomial在$z=93$点处的关系之后，Prover所剩的唯一一件事情是：

• 证明这些DEEP Polynomials是low-degree的。

对Verifier来说，FRI协议提供了一种确认多项式low-degree-ness的机制，Verifier继续非常少量的计算。为将多个多项式的low-degree-ness assertion，reduce为，仅需应用一次FRI协议，Prover需使用DEEP Mixing Parameter $b$（本例中，取$b=21$），来将多个DEEP Polynomials混合为单个FRI Polynomial：

• 令$c_1^{\prime },c_2^{\prime },c_3^{\prime },d_1^{\prime },d_2^{\prime },d_3^{\prime },V^{\prime }$来表示DEEP Polynomials，将这些DEEP Polynomials混合构建的FRI Polynomial为：$f(x)=b^0\ast c_1^{\prime }(x)+b^1\ast c_2^{\prime }(x)+\cdots +b^6\ast V^{\prime }(x)$。

为完整整个证明，Prover为“f(x)是low-degree多项式” 构建一个FRI proof。

这样，Prover就构建了a zero-knowledge argument of computation integrity，同时其验证速度快得令人难以置信。

7.3 FRI Folding and Queries

已知某vector commitment，FRI协议可证明该承诺值对应某low-degree多项式的evaluations。
在本例中，使用FRI来证明上一节的“FRI Polynomial” commitment具有的degree不超过7。

本例中的“FRI blow-up factor”为$4$，因此FRI Polynomial的承诺值有$32$个元素，且degree为$7$的多项式有$8$个系数。该blow-up factor为之前选择Reed-Solomon expansion的结果。FRI blow-up factor为$4$，对应的RS code rate为$1/4$。

FRI包括：

• 1）commit阶段：包含$r$轮。在每轮中，Prover会将之前的commitment "fold"为更小的commitment——既有更小的commitment size，也有更小的polynomial degree。

  • 如本例中，当使用的folding factor为$2$时，对应有3轮。每一轮中，Prover所承诺的向量的长度，为前一轮的一半。每一轮中，都通过先将系数切分为奇数和偶数部分，然后使用Verifier提供的随机值将这2部分混合，来完成folding。
    下图中展示了各轮中多项式的系数：
    

• 2）query阶段：本例中：

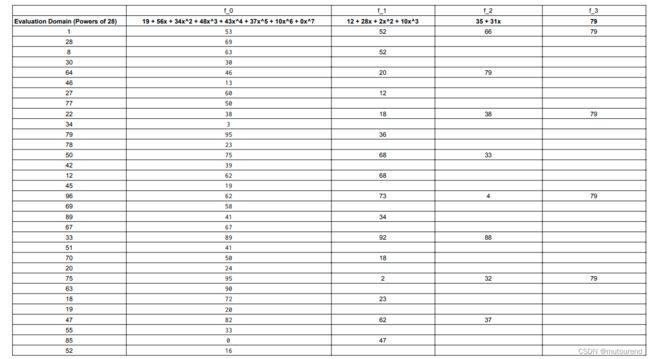
  • 在Prover分别 对$f_0$在powers of $28$、$f_1$在powers of $28^2$、$f_2$在powers of $28^4$、$f_3$在powers of $28^8$处的evaluations 完成了commit之后。【此处分别取$28,28^2,28^4,28^8$的原因在于，前面folding factor的取值为$2$。】
    • 因为$28$的multiplicative order为$32$，其对应的evaluation domains分别为$32$个元素、$16$个元素、$8$个元素、$4$个元素。
  • Verifier会做多个queries。这些queries用作随机挑战，用来测试Prover的commitments的合法性。
    • 宽泛来说，当blow-up factor为$4$时，单次query抓到Prover作弊的概率为$3/4$。换句话说，就是单次query提供了$2$个bits的安全性。
    • RISC Zero zkVM使用的blow-up factor为$4$，query次数为$50$，对应约为$100$-bit的安全性。

需注意，以上分析为完整安全性分析的简化，准确的安全等级不是正好$100$个bits。更详细地安全性分析参看RISC Zero zkVM 白皮书。

FRI Folding的关键点在于，其可checked locally：

• 对于单次query，Prover提供$f_0、f_1、f_2$的2个evaluation值，和$f_3$的一个evaluation值。
  • 如Verifier请求的query点为$g$，则Prover发送的evaluation值为：$f_0(\pm g)、f_1(\pm g^2)、f_2(\pm g^4)、f_3(g^8)$。
• Verifier在检查每个evaluation值的Merkle branch的同时，还会逐轮检查这些evaluation值的一致性。如，$f_1(g^2)$可表示为$f_0(g),f_0(-g)$以及该轮随机值 的组合。

7.3.1 Checking the Evaluations are Consistent

Verifier会通过如下公式来检查$f_{i-1}$与$f_i$的evaluation值的一致性：
$$f_i(x^2)=\frac{r_i+x}{2x}{f}_{i-1}(x)+\frac{r_i-x}{2(-x)}{f}_{i-1}(-x)$$

具体的推理过程为：
因：$f_1(x^2)=f_{0,even}(x^2)+r_1\cdot f_{0,odd}(x^2)$
即意味着：$f_1(x^2)=\frac{r_1+x}{2x}{f}_0(x)+\frac{r_1-x}{2(-x)}{f}_0(-x)$

其中：
$f_{0,even}(x^2)=\frac{f_0(x)+f_0(-x)}{2}$
$f_{0,odd}(x^2)=\frac{f_0(x)-f_0(-x)}{2x}$
从而有：$f_1(x^2)=f_{0,even}(x^2)+r_1\cdot f_{0,odd}(x^2)$
将$f_{0,even},f_{0,odd}$带入上面公式，仅使用$f_0(x),f_0(-x),r_1$来重写$f_1(x^2)$，有：
$f_1(x^2)=\frac{f_0(x)+f_0(-x)}{2}+r_1\cdot \frac{f_0(x)-f_0(-x)}{2x}$

找到共同的分母，并重新组合各项，有：
$f_1(x^2)=\frac{x{f}_0(x)+x{f}_0(-x)}{2x}+r_1\cdot \frac{f_0(x)-f_0(-x)}{2x}=\frac{r_1+x}{2x}{f}_0(x)+\frac{x-r_1}{2x}{f}_0(-x)=\frac{r_1+x}{2x}{f}_0(x)+\frac{r_1-x}{2(-x)}{f}_0(-x)$。

参考资料

[1] STARK by Hand
[2] RISC Zero doc STARK by Hand

RISC Zero系列博客

• RISC0：Towards a Unified Compilation Framework for Zero Knowledge
• Risc Zero ZKVM：zk-STARKs + RISC-V
• 2023年 ZK Hack以及ZK Summit 亮点记
• RISC Zero zkVM 白皮书
• Risc0：使用Continunations来证明任意EVM交易
• Zeth：首个Type 0 zkEVM
• RISC Zero项目简介
• RISC Zero zkVM性能指标
• Continuations：扩展RISC Zero zkVM支持（无限）大计算
• A summary on the FRI low degree test前2页导读
• Reed-Solomon Codes及其与RISC Zero zkVM的关系
• RISC Zero zkVM架构
• RISC-V与RISC Zero zkVM的关系
• 有限域的Fast Multiplication和Modular Reduction算法实现
• RISC Zero的Bonsai证明服务
• RISC Zero ZKP协议中的商多项式
• FRI的Commit、Query以及FRI Batching内部机制