算法模板之双链表图文详解
个人主页:聆风吟
系列专栏:算法模板、数据结构
少年有梦不应止于心动,更要付诸行动。
文章目录
- 前言
- 一. ⛳️使用数组模拟双链表讲解
-
- 1.1 为什么我们要使用数组去模拟双链表?
- 1.2 用数组模拟实现双链表
-
- 1.2.1 整体框架说明
- 1.2.2 双链表查找和修改
- 1.2.3 双链表插入结点
- 1.2.4 双链表删除结点
- 1.3 模板提取(重点)
-
- 1.3.1 有详细注释版
- 1.3.1 无详细注释版
- 二. ⛳️题目练习
-
- 2.1 题目
- 2.2 输入样例
- 2.3 输出样例
- 2.4 c++代码
- 结语
前言
hello! 各位铁子们大家好哇,今天作者给大家带来的算法模板是使用数组模拟双链表,让我们一起加油进步。
系列专栏:本期文章收录在《算法模板》,大家有兴趣可以浏览和关注,后面将会有更多精彩内容!
欢迎大家关注点赞收藏⭐️留言
一. ⛳️使用数组模拟双链表讲解
1.1 为什么我们要使用数组去模拟双链表?
由于该问题已经在第一期《算法模板之单链表讲解》这篇文章中已经叙述过了,相信看过第一期的小伙伴应该已经知道,在这里就不多阐述,感兴趣的小伙伴可以自行跳转浏览。
1.2 用数组模拟实现双链表
1.2.1 整体框架说明
初始状态:左边界结点指向右边界结点,右边界结点指向左边界结点

插入结点状态:
- 创建数组
val、pre和ne分别存储某个结点的值以及它的前驱指针和后继指针; - 下标 0 和 1 分别存储边界结点;
- 从下标 2 的位置开始插入结点;
- 本文仅仅使用左右边界结点的指针,无需在意其中存的值。
综上所述,真正的结点相当于从下标为2的位置开始往后所有插入的数,左右边界结点仅起到一个指针的效果。如下图的3,4,5,6为真正的结点。

1.2.2 双链表查找和修改
因为是使用数组模拟出来的链表,所以对于查找和修改直接通过数组下标进行遍历查找即可,这里就不多叙述。
1.2.3 双链表插入结点
在第k个结点的右边插入一个数 x:如下图在第2个结点后面插入一个数 7。
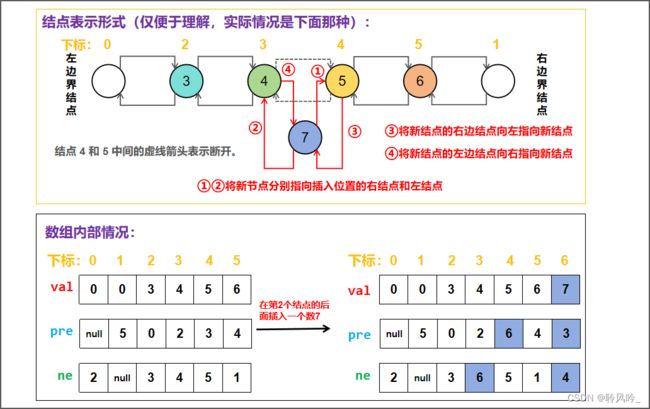
代码展示(建议结合图示看注释):
//在结点k的右边插入一个数x
void insert(int k, int x)
{
//将待插值赋给新结点
val[idx] = x;
//将新结点分别指向插入位置的右结点和左结点
ne[idx] = ne[k];
pre[idx] = k;
//将新结点的右边结点向左指向新结点
pre[ne[k]] = idx;
//将新结点的左边结点向右指向新结点
ne[k] = idx;
//更新结点索引
idx++;
}
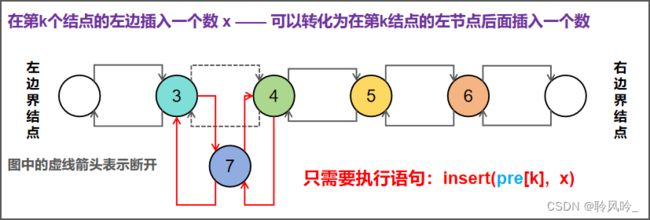
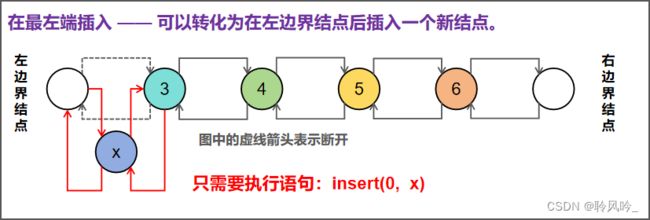
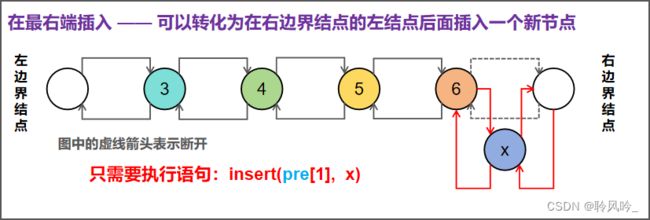
其他形式插入:在链表的最左端插入、最右端插入、在第k个结点的左边插入一个数 x
在其他位置插入,大家可以按照上面的方式自行模拟。不过,在算法竞赛中如果每种插入方式都模拟一下,显然是太浪费时间了。仔细观察可以发现,我们仍然可以使用上面的insert(int k, int x)函数实现各种位置的插入,只需要稍微变动一下传入的 k 值。
1.2.4 双链表删除结点
代码展示(建议结合图示看注释):
//删除第k个结点
void remove(int k)
{
//将待删除结点的左结点的后继指针指向待删除结点的右结点
ne[pre[k]] = ne[k];
//将待删除结点的右结点的前驱指针指向待删除结点的左结点
pre[ne[k]] = pre[k];
}
1.3 模板提取(重点)
1.3.1 有详细注释版
模板代码
// val[i] 表示结点i的值
// pre[i] 表示结点i的前驱指针
// ne[i] 表示结点i的后继指针
// idx 存储当前已经用到了哪个点,即记录当前下标位置
int val[N], pre[N], ne[N], idx;
//初始化
void init()
{
//左边界结点指向右边界结点,右边界结点指向左边界结点
ne[0] = 1;
pre[1] = 0;
//更新结点索引,因为下标0和1被左右边界结点占用。
idx = 2;
}
//在结点k的右边插入一个数x
//只使用本函数可以通过改变k的值,实现其他形式的插入。
void insert(int k, int x)
{
//将待插值赋给新结点
val[idx] = x;
//将新节点分别指向插入位置的右结点和左结点
ne[idx] = ne[k];
pre[idx] = k;
//将新结点右边一节点向左指向新结点
pre[ne[k]] = idx;
//将新结点左边一节点向右指向新结点
ne[k] = idx;
//更新结点索引
idx++;
}
//删除第k个结点
void remove(int k)
{
//将待删除结点的左结点的后继指针指向待删除结点的右结点
ne[pre[k]] = ne[k];
//将待删除结点的右结点的前驱指针指向待删除结点的左结点
pre[ne[k]] = pre[k];
}
1.3.1 无详细注释版
int val[N], pre[N], ne[N], idx;
//初始化
void init()
{
ne[0] = 1;
pre[1] = 0;
idx = 2;
}
//在结点k的右边插入一个数x
void insert(int k, int x)
{
val[idx] = x;
ne[idx] = ne[k];
pre[idx] = k;
pre[ne[k]] = idx;
ne[k] = idx;
idx++;
}
//删除第k个结点
void remove(int k)
{
ne[pre[k]] = ne[k];
pre[ne[k]] = pre[k];
}
二. ⛳️题目练习
⌈ 在线OJ链接,可以转至此处自行练习 ⌋
2.1 题目
![]()
2.2 输入样例
10
R 7
D 1
L 3
IL 2 10
D 3
IL 2 7
L 8
R 9
IL 4 7
IR 2 2
2.3 输出样例
8 7 7 3 2 9
2.4 c++代码
#include结语
今天的干货分享到这里就结束啦!如果觉得文章还可以的话,希望能给个三连支持一下,聆风吟的主页还有很多有趣的文章,欢迎小伙伴们前去点评,您的支持就是作者前进的最大动力!