Codeforces Round 915(Div.2) A~C(D,E更新中...)

A.Constructive Problems(思维)

题意：

给出一个$n\times m$的网格，你需要将网格上所有点均填满水，当一个格子同时满足以下两个条件时，格子中也会被填满水：

1. 该格子的左边或右边已经被填满水了

2. 该格子的上面或下面已经被填满水了

一次操作可以给一个格子填满水，问至少几次操作才能将所有网格填满。

分析：

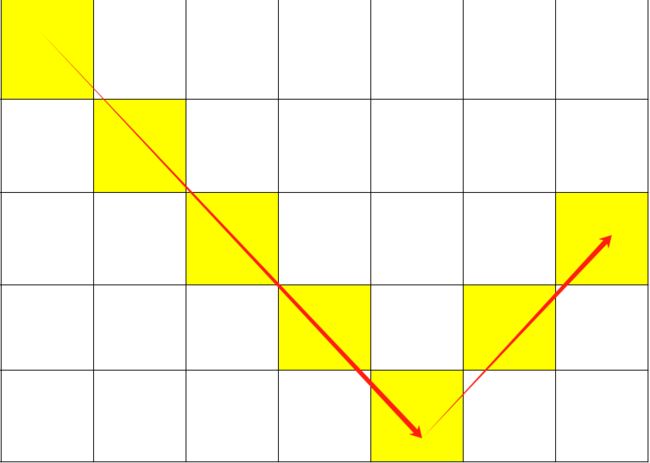
分析样例后可以发现，对于一个$n\times m$的网格，每行/列均只需要包含一个被填满水的格子就能保证所有格子中均被水覆盖，即答案为$max(n,m)$。

填充方案如下图：

代码：

#include 
using namespace std;

void solve() {
    int n, m;
    cin >> n >> m;
    cout << max(n, m) << endl;
}

int main() {
    int Case;
    cin >> Case;
    while (Case--) {
        solve();
    }
    return 0;
}

B.Begginer’s Zelda（思维）

题意：

给出一棵树，你可以继续若干次以下操作：

• 选择两个点$u$和$v$

• 然后将$u$到$v$之间的所有点删除（包括$u,v$），然后添加一个新的点代替原本的所有点，并连接原本所有点连着的边。

问至少需要多少次操作，才能使树上只剩下一个节点？

分析：

观察样例后可以发现，每次选择两个不同链上的叶节点，删除他们到达根节点的边，此时，由于叶节点所在的链被删除了，那么删除后不会产生新的叶节点，即树上的叶节点数量会减少$2$（当树上至少还包含$4$个叶节点时，如果树上只包含$3$个叶节点，不难发现删除后只会减少一个叶节点）。

那么，如果总叶结点数量为$k$，将叶节点删除到只剩$2$需要的次数为$\lfloor (k-1)/2\rfloor$，然后，只剩两个叶节点的树实际上就是一条链，此时再进行一次操作就能将树变为一个节点，因此，答案为$\lfloor (k-1)/2+1\rfloor =\lfloor (k+1)/2\rfloor$。

代码：

#include 
using namespace std;
typedef long long LL;
const int N = 1e5 + 5e2;

int n, ans;
vector<int> G[N];

void dfs(int root, int pre) {
    int len = G[root].size();
    if (len == 1) ans++;
    for (int i = 0; i < len; i++) {
        int v = G[root][i];
        if (v == pre) continue;
        dfs(v, root);
    }
}

void solve() {
    cin >> n;
    for (int i = 1; i <= n; i++) G[i].clear();
    for (int i = 1; i < n; i++) {
        int u, v;
        cin >> u >> v;
        G[u].push_back(v);
        G[v].push_back(u);
    }
    ans = 0;
    dfs(1, -1);
    cout << (ans + 1) / 2 << endl;
}

int main() {
    int Case;
    cin >> Case;
    while (Case--) {
        solve();
    }
    return 0;
}

C.Largest Subsequence（贪心）

题意：

给出一个长度为$n$的字符串$s$，字符串中仅包含小写字母，你可以进行若干次以下操作：

• 选择字符串$s$中的字典序最大的子序列$t$，并将该子序列向右旋转一次，即将$t_1{t}_2...t_m$变为$t_m{t}_1{t}_2...t_{m-1}$

问：最少操作几次可以使得该字符串被排序成增序，如果无法完成排序，输出$-1$.

分析：

不难发现，由于每次右移相当于在子序列中将最后的元素删除，那么操作后子序列仍然是字典序最大的，实际上能进行操作的始终是同一个字符串。

那么，只需要对该子序列进行排序，然后检查字符串排序后整个字符串$s$是否有序，如果有序，输出操作前字典序最大的子序列中包含的所有字符数量减去最大字符的数量（排序执行到最大元素到最后位置就结束了，因此该子序列中所有最大的元素是不需要操作次数的）。

否则，输出$-1$

代码：

#include 
using namespace std;
typedef long long LL;
const int N = 1e5 + 5e2;

vector<int> V[30];

void solve() {
    int n;
    string s;
    cin >> n >> s;
    for (int i = 0; i < 26; i++) V[i].clear();
    for (int i = 0; i < n; i++) {
        V[s[i] - 'a'].push_back(i);
    }
    int start_pos = -1, cnt = 0;
    vector<int> p;
    for (int i = 25; i >= 0; i--) {
        int pos = lower_bound(V[i].begin(), V[i].end(), start_pos) - V[i].begin();
        int len = V[i].size();
        if (pos >= len) continue;
        if (cnt == 0) cnt = V[i].size();
        for (int j = pos; j < len; j++) {
            p.push_back(V[i][j]);
        }
        start_pos = *(--p.end());
    }
    int len = p.size();
    for (int i = 0, j = len - 1; i < j; i++, j--) {
        swap(s[p[i]], s[p[j]]);
    }
    for (int i = 1; i < n; i++) {
        if (s[i] < s[i - 1]) {
            cout << "-1" << endl;
            return;
        }
    }
    cout << p.size() - cnt << endl;
}

int main() {
    int Case;
    cin >> Case;
    while (Case--) {
        solve();
    }
    return 0;
}

D,E 更新中…

学习交流

以下为学习交流QQ群，群号： 546235402，每周题解完成后都会转发到群中，大家可以加群一起交流做题思路，分享做题技巧，欢迎大家的加入。