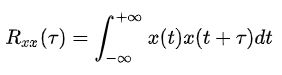使用相关序列方法做相位校准（附仿真代码）

        TI对天线幅相校准提出了标准的方法和流程，可参考这篇文档使用级联毫米波传感器的成像雷达参考设计1（TI文档）-CSDN博客的3.3节。这里使用自相关序列的方法来对相位做校准。

        自相关（Autocorrelation），也叫序列相关，是一个信号与其自身在不同时间点的互相关。非正式地来说，自相关是对同一信号在不同时间的两次观察，通过对比来评判两者的相似程度。自相关函数就是信号x(t)和它的时移信号x(t-τ)的乘积平均值。它是时移变量τ的函数。

        用数学的语言表述，则是：自相关函数是信号在时域中特性的平均度量，它用来描述信号在一个时刻的取值与另一时刻取值的依赖关系。数学上是这样定义的：

        

        假设有一个余弦信号： 

        根据定义，有：

        

        当相位相等时，相关曲线的幅值最大，可以利用这一特性来估算天线不同通道之间的相位差，然后做相位校准。

        这里以TI的AWR2944芯片为例，仿真4发4收DDMA模式下的天线通道相位校准。

        首先，生成16个虚拟接收通道的信号，由于目标位置相同，收到的信号除了相位，幅度和频率都一样，这样画图时就会混叠在一起，不方便观察，因此这里给每个信号添加一个直流偏置，使得每个通道的信号能从幅度上区分。

        增加直流分量的各通道信号如下，每个通道的余弦信号非常直观，可以看到每个信号的幅值、频率基本一样，但相位略有区别。

       对每个通道做FFT，可以看到每个通道的频谱，通过峰值搜索得到频率值。

        最后以第1各通道为基准，计算与所有通道的相关函数，通过给定不同时延（与相位线性变化），得到相关曲线。再搜索所有相关曲线的最大值，索引得到相位偏差值。

        计算结果表明，通过校准，平均相位误差可以调整到小于2°。

        完整代码如下。

% 发射波形和接收波形信号
clc;clear;
close all;
N = 16;                 % 通道数
L = 1000;               % 时域信号序列长度      
fs = 60000;             % 采样频率
ts = 1/fs;              % 采样时间间隔
t = ts:ts:L*ts;         % 时间序列
phase = 0:0.1*pi:(N-1)*0.1*pi;  % 每个通道的初始相位，单位弧度
A = 2.5:2.5:N*2.5;
s = zeros(N, L);        
ss = zeros(N, L);       % 增加直流分量用于区分显示
f = 259;                % 信号频率

for i = 1:N
    s(i,:) = cos(2*pi*f*t + phase(i)) + 0.1*randn(1,L);
    ss(i,:) = A(i) + s(i,:);
end
% 画出时域信号
figure;
plot(t, s);
grid on;
title('混叠在一起的16通道信号');
figure;
plot(t, ss);
grid on;
legend('1','2','3','4','5','6','7','8','9','10','11','12','13','14','15','16');
title('用直流幅度区分的16通道信号');

Nf = 65536;              % 计算FFT的点数
df = fs/Nf;              % 频率分辨率
s_fft = zeros(N,Nf);     % s的FFT结果 
for i = 1:N
    s_fft(i,:) = 10*log10(abs(fft(s(i,:),Nf)));
end
% 画出FFT幅值结果
figure;
for i = 1:N
    subplot(4,4,i);
    plot((1:Nf/2)*df,s_fft(i,(1:Nf/2)));
    ylim([-10,30]);
    grid on;
    title(num2str(i));
end
suptitle('FFT频率分析-dB');

% 通过最大幅值响应计算频率
[fft_max, index] = max(s_fft,[],2);
f_cal = index*df;
f_cal = mean(f_cal);
f_error = f_cal - f;

% 相移精度，单位°
d_phase = 360*f*ts;
min_dots = 360 / d_phase;
corr_num = floor(min_dots) + 1;
s_corr_sum = zeros(N,corr_num);
% 通过自相关（互相关）计算相移，这里只取一个周期用来计算
for i = 1:N
    for j = 1:corr_num
        s_corr = s(1,j:j+corr_num-1).*s(i,1:corr_num);
        s_corr_sum(i,j) = sum(s_corr);
    end
end
% 画出时域信号相关曲线
figure;
for i = 1:N
    subplot(4,4,i);
    plot(1:corr_num,s_corr_sum(i,:));
    grid on;
    title(num2str(i));
end
suptitle('第1通道为基准的相关曲线');

% 取自相关最大值索引为相移值
[max_sum,index] = max(s_corr_sum,[],2);
phase_cal = index*d_phase;
phase_error = phase_cal - phase'*180/pi;      % 这里单位转成°
phase_mean_error = mean(phase_error(2:N));

参考资料：

雷达编程实战之幅度与相位标定-CSDN博客

自相关与互相关_自相关和互相关-CSDN博客

互相关延时估计 Matlab仿真_互相关函数求时延原理-CSDN博客