秩的11个常用不等式(完全证明)——考试必考,面试必问2
秩的不等式
思路
本文默认读者了解矩阵秩的多种定义。如果不了解,也没关系,可以先移步博主的本篇文章。
-
思路1:证明秩相等,考虑证同解方程组
构造(Ⅰ) A X = 0 ⃗ AX = \vec{0} AX=0 (Ⅱ) B X = 0 ⃗ BX = \vec{0} BX=0 。( A , B A,B A,B 列数相同)
若(Ⅰ)(Ⅱ)同解(两个方程组,若它们的未知量个数相同且解集相等,则称为同解方程组),则(Ⅰ)(Ⅱ)各自的基础解系等价,从而 n − r ( A ) = n − r ( B ) ⇒ r ( A ) = r ( B ) n-r(A) = n-r(B) \Rightarrow r(A) = r(B) n−r(A)=n−r(B)⇒r(A)=r(B) (基础解系的秩加系数矩阵的秩等于 n n n,此篇博客有证明) 。
-
思路2: 证明秩不相等,可考虑向量组的表示问题,常用结论如下:
若 α 1 , α 2 , … , α s \bold{\alpha}_1,\bold{\alpha}_2,\dots,\bold{\alpha}_s α1,α2,…,αs 可由 β 1 , β 2 , … , β t \bold{\beta}_1,\bold{\beta}_2,\dots,\bold{\beta}_t β1,β2,…,βt 线性表示(表出),则 r ( α 1 , α 2 , … , α s ) ≤ r ( β 1 , β 2 , … , β t ) r(\bold{\alpha}_1,\bold{\alpha}_2,\dots,\bold{\alpha}_s)\le r(\bold{\beta}_1,\bold{\beta}_2,\dots,\bold{\beta}_t) r(α1,α2,…,αs)≤r(β1,β2,…,βt)
-
思路3:初等变换不改变矩阵的秩,利用初等变换将矩阵化为阶梯形,阶梯形矩阵非零行的行数目就是矩阵的秩。
-
思路4:分块矩阵的初等变换不改变矩阵的秩。构造分块矩阵,利用分块矩阵的初等变换及分块矩阵的秩的相关定理去求解。构造分块矩阵是难点,如结论10.
-
思路5:寻找矩阵 A A A 的最高阶非零子式的阶数,即为矩阵的秩。
常用不等式
设 A A A 为 m × n m\times n m×n 的矩阵, B B B 为满足矩阵运算要求的矩阵,则下列结论成立:
结论1
0 ≤ r ( A ) ≤ m i n { m , n } r ( A ) = 0 ⇔ A = 0 ⃗ 0 \le r(A)\le min\{m,n\}\\ r(A) = 0 \Leftrightarrow A = \vec{0} 0≤r(A)≤min{m,n}r(A)=0⇔A=0
结论2
r ( k A ) = r ( A ) ( k ≠ 0 ) r(kA)=r(A) \qquad (k \ne 0 ) r(kA)=r(A)(k=0)
证明:(法1)构造(Ⅰ) A X = 0 ⃗ AX = \vec{0} AX=0 (Ⅱ) k A X = 0 ⃗ kAX = \vec{0} kAX=0
(1)若 ξ \xi ξ 为(Ⅰ) 的任一解,则 A ξ = 0 ⃗ ⇒ k A ξ = 0 ⃗ A\xi = \vec{0} \Rightarrow kA\xi = \vec{0} Aξ=0⇒kAξ=0 ,故 ξ \xi ξ 也为(Ⅱ)的解;
(2)若 η \eta η 为(Ⅱ) 的任一解,则 k A η = 0 ⃗ kA\eta = \vec{0} kAη=0 ,又 k ≠ 0 k \ne 0 k=0,故 A η = 0 ⃗ A\eta = \vec{0} Aη=0, η \eta η 也为(Ⅰ)的解;
综合(1)(2),得(Ⅰ)(Ⅱ)同解,故结论2成立。
(法2)当 k ≠ 0 k \ne 0 k=0 时, k A kA kA 和 A A A 最高非零子式的阶数相同,故 结论2成立。
结论3
r ( A ) = r ( A T ) = r ( A A T ) = r ( A T A ) r(A) = r(A^{T})=r(AA^{T})=r(A^{T}A) r(A)=r(AT)=r(AAT)=r(ATA)
证明: ∀ A m × n , A m × n T A m × n = ( A T A ) n × n \forall A_{m\times n},\quad A_{m\times n}^{T}A_{m\times n}=(A^{T}A)_{n\times n} ∀Am×n,Am×nTAm×n=(ATA)n×n
A A A 与 A T A A^{T}A ATA 列数相同;
构造(Ⅰ) A X = 0 ⃗ AX = \vec{0} AX=0 (Ⅱ) A T A X = 0 ⃗ A^{T}AX = \vec{0} ATAX=0
(1)若 ξ \xi ξ 为(Ⅰ) 的任一解,则 A ξ = 0 ⃗ ⇒ A T A ξ = A T 0 ⃗ = 0 ⃗ A\xi = \vec{0} \Rightarrow A^{T}A\xi = A^{T}\vec{0}=\vec{0} Aξ=0⇒ATAξ=AT0=0 ,故 ξ \xi ξ 也为(Ⅱ)的解;
(2)若 η \eta η 为(Ⅱ) 的任一解,则
A T A η = 0 ⃗ ⇒ η T A T A η = η T 0 ⃗ = 0 ⇒ ( A η ) T A η = 0 ⇒ ∣ ∣ A η ∣ ∣ 2 = 0 ⇔ A η = 0 ⃗ A^{T}A\eta = \vec{0} \Rightarrow \eta^{T}A^{T}A\eta = \eta^{T}\vec{0}=0\Rightarrow (A\eta)^{T}A\eta = 0 \Rightarrow ||A\eta||^{2}=0 \Leftrightarrow A\eta=\vec{0} ATAη=0⇒ηTATAη=ηT0=0⇒(Aη)TAη=0⇒∣∣Aη∣∣2=0⇔Aη=0
故 η \eta η 也为(Ⅰ)的解;
综合(1)(2),得(Ⅰ)(Ⅱ)同解,故 r ( A ) = r ( A T A ) r(A) = r(A^{T}A) r(A)=r(ATA)。
另一方面,显然 r ( A ) = r ( A T ) r(A) = r(A^{T}) r(A)=r(AT) ,又 r ( A ) = r ( A T A ) ⇒ r ( A T ) = r ( A A T ) r(A) = r(A^{T}A) \Rightarrow r(A^T) = r(AA^{T}) r(A)=r(ATA)⇒r(AT)=r(AAT)
故结论3成立。
结论4
对于 n × n n \times n n×n 矩阵 A A A ,有 r ( A n ) = r ( A n + 1 ) r(A^{n}) = r(A^{n+1}) r(An)=r(An+1)
证明 构造(Ⅰ) A n X = 0 ⃗ A^{n}X = \vec{0} AnX=0 (Ⅱ) A n + 1 X = 0 ⃗ A^{n+1}X = \vec{0} An+1X=0
(1)若 ξ \xi ξ 为(Ⅰ) 的任一解,则 A n ξ = 0 ⃗ ⇒ A × A n ξ = A × 0 ⃗ = 0 ⃗ A^{n}\xi = \vec{0} \Rightarrow A\times A^{n}\xi=A\times\vec{0}=\vec{0} Anξ=0⇒A×Anξ=A×0=0, 故 ξ \xi ξ 也为(Ⅱ)的解;
(2)若 η \eta η 为(Ⅱ) 的任一解,则 有 A n + 1 η = 0 ⃗ A^{n+1}\eta = \vec{0} An+1η=0 , 假设 A n η ≠ 0 ⃗ A^{n}\eta \ne \vec{0} Anη=0
设 ∃ k 0 , k 1 , k 2 , … , k n \exist k_0,k_1,k_2,\dots, k_n ∃k0,k1,k2,…,kn 使得 k 0 η + k 1 A η + k 2 A 2 η + ⋯ + k n A n η = 0 ⃗ k_0\eta+k_1A\eta+k_2A^{2}\eta+\dots+k_nA^{n}\eta = \vec{0} k0η+k1Aη+k2A2η+⋯+knAnη=0 (一定可以让等式成立,最差是系数全为0)。
左乘 A n A^{n} An ,有 k 0 A n η + k 1 A n + 1 η + k 2 A n + 2 η + ⋯ + k n A n + n η = A n × 0 ⃗ = 0 ⃗ k_0A^{n}\eta+k_1A^{n+1}\eta+k_2A^{n+2}\eta+\dots+k_nA^{n+n}\eta = A^{n}\times \vec{0}=\vec{0} k0Anη+k1An+1η+k2An+2η+⋯+knAn+nη=An×0=0
结合方程(Ⅱ),推出 k 0 A n η = 0 ⇒ k 0 = 0 k_0A^{n}\eta = 0 \Rightarrow k_{0}=0 k0Anη=0⇒k0=0 结合假设 ⇒ k 1 A η + k 2 A 2 η + ⋯ + k n A n η = 0 ⃗ \Rightarrow k_1A\eta+k_2A^{2}\eta+\dots+k_nA^{n}\eta = \vec{0} ⇒k1Aη+k2A2η+⋯+knAnη=0
左乘 A n − 1 A^{n-1} An−1 ,有 k 1 A n η + k 2 A n + 1 η + ⋯ + k n A n + n − 1 η = A n − 1 × 0 ⃗ = 0 ⃗ k_1A^{n}\eta+k_2A^{n+1}\eta+\dots+k_nA^{n+n-1}\eta = A^{n-1}\times \vec{0}=\vec{0} k1Anη+k2An+1η+⋯+knAn+n−1η=An−1×0=0
结合方程(Ⅱ),推出 k 1 = 0 k_{1} = 0 k1=0 。
以此类推,有 k 2 = k 3 = ⋯ = k n = 0 k_{2}=k_{3}=\dots =k_{n}=0 k2=k3=⋯=kn=0 ,故 η , A η , A 2 η , … , A n η \eta,A\eta,A^{2}\eta,\dots,A^{n}\eta η,Aη,A2η,…,Anη 线性无关。又 n + 1 n+1 n+1 个 n n n 维向量必定线性相关,矛盾,所以假设不成立,立即有
A n η = 0 ⃗ A^{n}\eta = \vec{0} Anη=0
故 η \eta η 为(Ⅰ) 的解。
综合(1)(2),得(Ⅰ) (Ⅱ) 同解,故 r ( A n ) = r ( A n + 1 ) r(A^{n}) = r(A^{n+1}) r(An)=r(An+1)
结论5
m a x { r ( A ) , r ( B ) } ≤ r ( A , B ) ≤ r ( A ) + r ( B ) max\{r(A),r(B)\} \le r(A,B) \le r(A)+r(B) max{r(A),r(B)}≤r(A,B)≤r(A)+r(B)
注: r ( A , B ) r(A,B) r(A,B) 是求 矩阵 [ A B ] [A \quad B] [AB] 的秩。
证明:(1)显然 r ( A ) ≤ r ( A , B ) r(A) \le r(A,B) r(A)≤r(A,B) 而且 r ( B ) ≤ r ( A , B ) r(B) \le r(A,B) r(B)≤r(A,B) ,故 m a x { r ( A ) , r ( B ) } ≤ r ( A , B ) max\{r(A),r(B)\} \le r(A,B) max{r(A),r(B)}≤r(A,B)
(2)设 r ( A m × n ) = p , r ( B m × n ) = q r(A_{m\times n}) = p, r(B_{m\times n}) = q r(Am×n)=p,r(Bm×n)=q
将 A , B A,B A,B 按列分块为 A = ( α 1 , α 2 , … , α n ) A=(\bold{\alpha}_{1},\bold{\alpha}_{2},\dots,\bold{\alpha}_{n}) A=(α1,α2,…,αn) , B = ( β 1 , β 2 , … , β n ) B=(\bold{\beta}_{1},\bold{\beta}_{2},\dots,\bold{\beta}_{n}) B=(β1,β2,…,βn),
于是 ( A , B ) = ( α 1 , α 2 , … , α n , β 1 , β 2 , … , β n ) (A,B)=(\bold{\alpha}_{1},\bold{\alpha}_{2},\dots,\bold{\alpha}_{n},\bold{\beta}_{1},\bold{\beta}_{2},\dots,\bold{\beta}_{n}) (A,B)=(α1,α2,…,αn,β1,β2,…,βn) 。
不妨设 A , B A,B A,B 的列向量组的极大线性无关组分别为 α 1 , α 2 , … , α p \bold{\alpha}_{1},\bold{\alpha}_{2},\dots,\bold{\alpha}_{p} α1,α2,…,αp和 β 1 , β 2 , … , β q \bold{\beta}_{1},\bold{\beta}_{2},\dots,\bold{\beta}_{q} β1,β2,…,βq ,
显然 α 1 , α 2 , … , α n , β 1 , β 2 , … , β n \bold{\alpha}_{1},\bold{\alpha}_{2},\dots,\bold{\alpha}_{n},\bold{\beta}_{1},\bold{\beta}_{2},\dots,\bold{\beta}_{n} α1,α2,…,αn,β1,β2,…,βn 可由 α 1 , α 2 , … , α p , β 1 , β 2 , … , β q \bold{\alpha}_{1},\bold{\alpha}_{2},\dots,\bold{\alpha}_{p},\bold{\beta}_{1},\bold{\beta}_{2},\dots,\bold{\beta}_{q} α1,α2,…,αp,β1,β2,…,βq 线性表示,故
r ( α 1 , α 2 , … , α n , β 1 , β 2 , … , β n ) ≤ r ( α 1 , α 2 , … , α p , β 1 , β 2 , … , β q ) ≤ p + q r(\bold{\alpha}_{1},\bold{\alpha}_{2},\dots,\bold{\alpha}_{n},\bold{\beta}_{1},\bold{\beta}_{2},\dots,\bold{\beta}_{n})\le r(\bold{\alpha}_{1},\bold{\alpha}_{2},\dots,\bold{\alpha}_{p},\bold{\beta}_{1},\bold{\beta}_{2},\dots,\bold{\beta}_{q})\le p+q r(α1,α2,…,αn,β1,β2,…,βn)≤r(α1,α2,…,αp,β1,β2,…,βq)≤p+q
故 r ( A , B ) ≤ r ( A ) + r ( B ) r(A,B)\le r(A)+r(B) r(A,B)≤r(A)+r(B) ,综合(1)(2),得结论5成立。
结论6
r ( A + B ) ≤ r ( A , B ) r(A+B) \le r(A,B) r(A+B)≤r(A,B)
证明:(法1)将 A , B A,B A,B 按列分块为 A = ( α 1 , α 2 , … , α n ) A=(\bold{\alpha}_{1},\bold{\alpha}_{2},\dots,\bold{\alpha}_{n}) A=(α1,α2,…,αn) , B = ( β 1 , β 2 , … , β n ) B=(\bold{\beta}_{1},\bold{\beta}_{2},\dots,\bold{\beta}_{n}) B=(β1,β2,…,βn),
于是 A + B = ( α 1 + β 1 , α 2 + β 2 , … , α n + β n ) A+B = (\bold{\alpha}_{1}+\bold{\beta}_{1},\bold{\alpha}_{2}+\bold{\beta}_{2},\dots,\bold{\alpha}_{n}+\bold{\beta}_{n}) A+B=(α1+β1,α2+β2,…,αn+βn) , ( A , B ) = ( α 1 , α 2 , … , α n , β 1 , β 2 , … , β n ) (A,B)=(\bold{\alpha}_{1},\bold{\alpha}_{2},\dots,\bold{\alpha}_{n},\bold{\beta}_{1},\bold{\beta}_{2},\dots,\bold{\beta}_{n}) (A,B)=(α1,α2,…,αn,β1,β2,…,βn) ,
显然 α 1 + β 1 , α 2 + β 2 , … , α n + β n \bold{\alpha}_{1}+\bold{\beta}_{1},\bold{\alpha}_{2}+\bold{\beta}_{2},\dots,\bold{\alpha}_{n}+\bold{\beta}_{n} α1+β1,α2+β2,…,αn+βn 可由向量组 α 1 , α 2 , … , α n , β 1 , β 2 , … , β n \bold{\alpha}_{1},\bold{\alpha}_{2},\dots,\bold{\alpha}_{n},\bold{\beta}_{1},\bold{\beta}_{2},\dots,\bold{\beta}_{n} α1,α2,…,αn,β1,β2,…,βn 线性表示
故 结论6成立
(法2)由分块矩阵的初等变换,得 r ( A + B , B ) → ( A , B ) r(A+B,B)\rightarrow (A,B) r(A+B,B)→(A,B) (初等列变换,把广义的第二列乘负一加到广义第一列),由于初等变换不改变矩阵的秩,故 r ( A + B ) ≤ r ( A + B , B ) = r ( A , B ) r(A+B)\le r(A+B,B)=r(A,B) r(A+B)≤r(A+B,B)=r(A,B) 得证。
结论7
r ( A B ) ≤ m i n { r ( A ) , r ( B ) } r(AB) \le min\{r(A),r(B)\} r(AB)≤min{r(A),r(B)}
证明: m × n m\times n m×n 矩阵 A = ( a i j ) A = (a_{ij}) A=(aij) 按列分块得
A = ( α 1 , α 2 , … , α n ) A = (\bold{\alpha}_{1},\bold{\alpha}_{2},\dots,\bold{\alpha}_{n}) A=(α1,α2,…,αn)
n × t n \times t n×t 矩阵 B = ( b i j ) B=(b_{ij}) B=(bij) 按行分块得
B = ( β 1 β 2 ⋮ β n ) B = \begin{pmatrix}\bold{\beta}_{1}\\\bold{\beta}_{2}\\ \vdots \\\bold{\beta}_{n}\end{pmatrix} B=⎝ ⎛β1β2⋮βn⎠ ⎞
注意,上面对 A , B A,B A,B 分别分块是在两部分证明中分别用到,它们不会出现在同一个等式中。同样,下面的等式中含 ξ i i = 1 , 2 , … t \xi_{i} \quad i=1,2,\dots t ξii=1,2,…t 和 η j j = 1 , 2 , … m \eta_{j} \quad j=1,2,\dots m ηjj=1,2,…m 的向量分别是对应对 A A A 按列分块和 B B B 按行分块时等式等号右边的分块矩阵。
A B = C = ( ξ 1 , ξ 2 , … , ξ t ) = ( η 1 η 2 ⋮ η m ) AB=C =(\xi_{1},\xi_{2},\dots,\xi_{t})=\begin{pmatrix}\bold{\eta}_{1}\\\bold{\eta}_{2}\\ \vdots \\\bold{\eta}_{m}\end{pmatrix} AB=C=(ξ1,ξ2,…,ξt)=⎝ ⎛η1η2⋮ηm⎠ ⎞
(1)
A B = ( α 1 , α 2 , … , α n ) ( b 11 b 12 … b 1 t b 21 b 22 … b 2 t ⋮ ⋮ b n 1 b n 2 … b n t ) = ( b 11 α 1 + b 21 α 2 + ⋯ + b n 1 α n , + b 12 α 1 + b 22 α 2 + ⋯ + b n 2 α n , … , b 1 t α 1 + b 2 t α 2 + ⋯ + b n t α n ) \begin{aligned} AB &=(\bold{\alpha}_{1},\bold{\alpha}_{2},\dots,\bold{\alpha}_{n}) \begin{pmatrix} b_{11}&b_{12}\dots b_{1t} \\ b_{21}&b_{22}\dots b_{2t} \\ \vdots & \vdots \\ b_{n1}&b_{n2}\dots b_{nt} \end{pmatrix}\\ &=(b_{11}\bold{\alpha}_{1}+b_{21}\bold{\alpha}_{2}+\dots+b_{n1}\bold{\alpha}_{n}, +b_{12}\bold{\alpha}_{1}+b_{22}\bold{\alpha}_{2}+\dots+b_{n2}\bold{\alpha}_{n},\dots,b_{1t}\bold{\alpha}_{1}+b_{2t}\bold{\alpha}_{2}+\dots+b_{nt}\bold{\alpha}_{n}) \end{aligned} AB=(α1,α2,…,αn)⎝ ⎛b11b21⋮bn1b12…b1tb22…b2t⋮bn2…bnt⎠ ⎞=(b11α1+b21α2+⋯+bn1αn,+b12α1+b22α2+⋯+bn2αn,…,b1tα1+b2tα2+⋯+bntαn)
所以 A B AB AB 的列向量 ξ 1 , ξ 2 , … , ξ t \xi_{1},\xi_{2},\dots,\xi_{t} ξ1,ξ2,…,ξt 可由 A A A 的列向量 α 1 , α 2 , … , α n \bold{\alpha}_{1},\bold{\alpha}_{2},\dots,\bold{\alpha}_{n} α1,α2,…,αn 线性表示,故
r ( ξ 1 , ξ 2 , … , ξ t ) ≤ r ( α 1 , α 2 , … , α n ) r(\xi_{1},\xi_{2},\dots,\xi_{t}) \le r(\bold{\alpha}_{1},\bold{\alpha}_{2},\dots,\bold{\alpha}_{n}) r(ξ1,ξ2,…,ξt)≤r(α1,α2,…,αn)
即 r ( A B ) ≤ r ( A ) r(AB)\le r(A) r(AB)≤r(A)
(2)
A B = ( a 11 a 12 … a 1 n a 21 a 22 … a 2 n ⋮ ⋮ a m 1 a m 2 … b m n ) ( β 1 β 2 ⋮ β n ) = ( a 11 β 1 + a 12 β 2 + ⋯ + a 1 n β n a 21 β 1 + a 22 β 2 + ⋯ + a 2 n β n ⋮ a m 1 β 1 + a m 2 β 2 + ⋯ + a m n β n ) = ( η 1 η 2 ⋮ η m ) = C m × t \begin{aligned} AB &= \begin{pmatrix} a_{11}&a_{12}\dots a_{1n} \\ a_{21}&a_{22}\dots a_{2n} \\ \vdots & \vdots \\ a_{m1}&a_{m2}\dots b_{mn} \end{pmatrix} \begin{pmatrix}\bold{\beta}_{1}\\\bold{\beta}_{2}\\ \vdots \\\bold{\beta}_{n}\end{pmatrix}\\ &= \begin{pmatrix}a_{11}\bold{\beta}_{1}+a_{12}\bold{\beta}_{2}+\dots+a_{1n}\bold{\beta}_{n}\\ a_{21}\bold{\beta}_{1}+a_{22}\bold{\beta}_{2}+\dots+a_{2n}\bold{\beta}_{n}\\ \vdots\\ a_{m1}\bold{\beta}_{1}+a_{m2}\bold{\beta}_{2}+\dots+a_{mn}\bold{\beta}_{n}\\ \end{pmatrix}\\ &=\begin{pmatrix}\bold{\eta}_{1}\\\bold{\eta}_{2}\\ \vdots \\\bold{\eta}_{m}\end{pmatrix} \\&= C_{m\times t} \end{aligned} AB=⎝ ⎛a11a21⋮am1a12…a1na22…a2n⋮am2…bmn⎠ ⎞⎝ ⎛β1β2⋮βn⎠ ⎞=⎝ ⎛a11β1+a12β2+⋯+a1nβna21β1+a22β2+⋯+a2nβn⋮am1β1+am2β2+⋯+amnβn⎠ ⎞=⎝ ⎛η1η2⋮ηm⎠ ⎞=Cm×t
所以 A B AB AB 的行向量 η 1 , η 2 , … , η m \bold{\eta}_{1},\bold{\eta}_{2},\dots,\bold{\eta}_{m} η1,η2,…,ηm 可由 B B B 的行向量 β 1 , β 2 , … , β n \bold{\beta}_{1},\bold{\beta}_{2},\dots,\bold{\beta}_{n} β1,β2,…,βn 线性表示,
故 r ( η 1 , η 2 , … , η m ) ≤ r ( β 1 , β 2 , … , β n ) r(\bold{\eta}_{1},\bold{\eta}_{2},\dots,\bold{\eta}_{m}) \le r(\bold{\beta}_{1},\bold{\beta}_{2},\dots,\bold{\beta}_{n}) r(η1,η2,…,ηm)≤r(β1,β2,…,βn),即 r ( A B ) ≤ r ( B ) r(AB) \le r(B) r(AB)≤r(B)
综合(1)(2),得结论7成立。
结论8
r ( ( A O O B ) ) = r ( A ) + r ( B ) r(\begin{pmatrix} \bold{A}&\bold{O}\\ \bold{O}&\bold{B} \end{pmatrix} ) = r(\bold{A})+r(\bold{B}) r((AOOB))=r(A)+r(B)
注:矩阵为分块矩阵。
证明:设 r ( A ) = p , r ( B ) = q r(\bold{A}) = p,\quad r(\bold{B}) = q r(A)=p,r(B)=q ,则
( A O O B ) → ( E p + q O O O ) \begin{pmatrix} \bold{A}&\bold{O}\\ \bold{O}&\bold{B} \end{pmatrix} \rightarrow \begin{pmatrix} \bold{E}_{p+q}&\bold{O}\\ \bold{O}&\bold{O} \end{pmatrix} (AOOB)→(Ep+qOOO)
因为初等不换不改变矩阵的秩,故
r ( ( A O O B ) ) = r ( ( E p + q O O O ) ) = p + q = r ( A ) + r ( B ) r(\begin{pmatrix} \bold{A}&\bold{O}\\ \bold{O}&\bold{B} \end{pmatrix} ) = r(\begin{pmatrix} \bold{E}_{p+q}&\bold{O}\\ \bold{O}&\bold{O} \end{pmatrix}) =p+q=r(\bold{A})+r(\bold{B}) r((AOOB))=r((Ep+qOOO))=p+q=r(A)+r(B)
结论8得证。
结论9
r ( A ) + r ( B ) ≤ r ( ( A O C B ) ) ≤ r ( A ) + r ( B ) + r ( C ) r(\bold{A})+r(\bold{B}) \le r(\begin{pmatrix} \bold{A}&\bold{O}\\ \bold{C}&\bold{B} \end{pmatrix} ) \le r(\bold{A})+r(\bold{B}) +r(\bold{C}) r(A)+r(B)≤r((ACOB))≤r(A)+r(B)+r(C)
证明:首先, r ( A ) + r ( B ) = r ( ( A O O B ) ) ≤ r ( ( A O C B ) r(\bold{A})+r(\bold{B}) = r(\begin{pmatrix} \bold{A}&\bold{O}\\ \bold{O}&\bold{B} \end{pmatrix} ) \le r(\begin{pmatrix} \bold{A}&\bold{O}\\ \bold{C}&\bold{B} \end{pmatrix} r(A)+r(B)=r((AOOB))≤r((ACOB)
另一方面 r ( ( A O C B ) ≤ r ( ( A C ) ) + r ( ( O B ) ) ≤ r ( A ) + r ( B ) + r ( C ) r(\begin{pmatrix} \bold{A}&\bold{O}\\ \bold{C}&\bold{B} \end{pmatrix} \le r(\begin{pmatrix} \bold{A} \\ \bold{C}\end{pmatrix})+r(\begin{pmatrix} \bold{O} \\ \bold{B}\end{pmatrix}) \le r(\bold{A})+r(\bold{B})+r(\bold{C}) r((ACOB)≤r((AC))+r((OB))≤r(A)+r(B)+r(C)
或者
r ( ( A O C B ) = r ( [ ( A O O B ) + ( O O C O ) ] ) ≤ r ( ( A O O B ) ) + r ( ( O O C O ) ) = r ( A ) + r ( B ) + r ( C ) r(\begin{pmatrix} \bold{A}&\bold{O}\\ \bold{C}&\bold{B} \end{pmatrix}=r(\begin{bmatrix} \begin{pmatrix} \bold{A}&\bold{O}\\ \bold{O}&\bold{B} \end{pmatrix}+\begin{pmatrix} \bold{O}&\bold{O}\\ \bold{C}&\bold{O} \end{pmatrix}\end{bmatrix})\\ \le r(\begin{pmatrix} \bold{A}&\bold{O}\\ \bold{O}&\bold{B} \end{pmatrix})+r(\begin{pmatrix} \bold{O}&\bold{O}\\ \bold{C}&\bold{O} \end{pmatrix})=r(\bold{A})+r(\bold{B})+r(\bold{C}) r((ACOB)=r([(AOOB)+(OCOO)])≤r((AOOB))+r((OCOO))=r(A)+r(B)+r(C)
故结论9得证。
结论10
r ( A B ) ≥ r ( A ) + r ( B ) − n r(AB) \ge r(A)+r(B)-n r(AB)≥r(A)+r(B)−n
证明:构造分块矩阵
( A B O O E n ) \begin{pmatrix} \bold{AB}&\bold{O}\\ \bold{O}&\bold{E}_{n} \end{pmatrix} (ABOOEn)
则 r ( ( A B O O E n ) ) = r ( A B ) + n r(\begin{pmatrix} \bold{AB}&\bold{O}\\ \bold{O}&\bold{E}_{n} \end{pmatrix}) = r(\bold{AB})+n r((ABOOEn))=r(AB)+n,(利用列向量的极大无关组)。
由分块矩阵的初等变换,得
注:关于分块矩阵的初等变换详细定义见附录,但其实和普通矩阵类似。
( A B O O E n ) → ( A B A O E n ) \begin{pmatrix} \bold{AB}&\bold{O}\\ \bold{O}&\bold{E}_{n} \end{pmatrix} \rightarrow \begin{pmatrix} \bold{AB}&\bold{A}\\ \bold{O}&\bold{E}_{n} \end{pmatrix} (ABOOEn)→(ABOAEn)
上面从左边变为右边,只需要初等行变换。
( A B A O E n ) → ( O A − B E n ) \begin{pmatrix}\bold{AB}&\bold{A}\\\bold{O}&\bold{E}_{n}\end{pmatrix}\rightarrow \begin{pmatrix}\bold{O}&\bold{A}\\\bold{-B}&\bold{E}_{n}\end{pmatrix} (ABOAEn)→(O−BAEn)
上面从左边变为右边,以 − B -B −B 右乘第二列加到第一列即可。
( O A − B E n ) → ( A O E n B ) \begin{pmatrix}\bold{O}&\bold{A}\\\bold{-B}&\bold{E}_{n}\end{pmatrix} \rightarrow \begin{pmatrix}\bold{A}&\bold{O}\\\bold{E}_{n}&\bold{B}\end{pmatrix} (O−BAEn)→(AEnOB)
上面从左边变为右边,首先用 − E -E −E 右乘第一列,然后再交换第1列和第二列。
因为初等变换不改变矩阵的秩,故
r ( A B ) + n = r ( ( A B O O E n ) ) = r ( ( A O E n B ) ) ≥ r ( A ) + r ( B ) r(\bold{AB})+n=r(\begin{pmatrix} \bold{AB}&\bold{O}\\ \bold{O}&\bold{E}_{n} \end{pmatrix})=r( \begin{pmatrix}\bold{A}&\bold{O}\\\bold{E}_{n}&\bold{B}\end{pmatrix}) \ge r(\bold{A})+r(\bold{B}) r(AB)+n=r((ABOOEn))=r((AEnOB))≥r(A)+r(B)
推出 r ( A B ) + n ≥ r ( A ) + r ( B ) r(\bold{AB})+n \ge r(\bold{A})+r(\bold{B}) r(AB)+n≥r(A)+r(B)
结论10成立。
结论11
若 A B = O AB = \bold{O} AB=O ,则 r ( A ) + r ( B ) ≤ n r(A)+r(B) \le n r(A)+r(B)≤n ,其中 n n n 是 A A A 的列数(或者 B B B 的行数)。
证明:(法1)对于 m × n m\times n m×n 矩阵 A A A , n × t n\times t n×t 矩阵 B B B, 记 B = ( β 1 , β 2 , … , β t ) B=(\bold{\beta}_{1},\bold{\beta}_{2},\dots,\bold{\beta}_{t}) B=(β1,β2,…,βt) ,则有
A B = A ( β 1 , β 2 , … , β t ) = ( A β 1 , A β 2 , … , A β t ) = O = ( 0 ⃗ , 0 ⃗ , … , 0 ⃗ ) \begin{aligned} AB &= A(\bold{\beta}_{1},\bold{\beta}_{2},\dots,\bold{\beta}_{t}) \\&=(A\bold{\beta}_{1},A\bold{\beta}_{2},\dots,A\bold{\beta}_{t}) \\&= \bold{O} \\ &= (\vec{0},\vec{0},\dots,\vec{0}) \end{aligned} AB=A(β1,β2,…,βt)=(Aβ1,Aβ2,…,Aβt)=O=(0,0,…,0)
故
A β i = 0 ⃗ i = 1 , 2 , … , t A\bold{\beta}_{i} = \vec{0} \quad i=1,2,\dots,t Aβi=0i=1,2,…,t
故 β 1 , β 2 , … , β t \bold{\beta}_{1},\bold{\beta}_{2},\dots,\bold{\beta}_{t} β1,β2,…,βt 为方程 A x = 0 ⃗ Ax=\vec{0} Ax=0 的部分解 ;
⇒ n − r ( A ) = r ( 全部解 ) ≥ r ( 部分解 ) = r ( β 1 , β 2 , … , β t ) = r ( B ) \Rightarrow n-r(A)= r(全部解) \ge r(部分解) =r(\bold{\beta}_{1},\bold{\beta}_{2},\dots,\bold{\beta}_{t}) =r(B) ⇒n−r(A)=r(全部解)≥r(部分解)=r(β1,β2,…,βt)=r(B)
⇒ r ( A ) + r ( B ) ≤ n \Rightarrow r(A)+r(B) \le n ⇒r(A)+r(B)≤n 得证。
(法2),利用结论10,
r ( A B ) ≥ r ( A ) + r ( B ) − n r(AB) \ge r(A)+r(B)-n r(AB)≥r(A)+r(B)−n
若 A B = O AB=\bold{O} AB=O ,则 r ( A B ) = 0 r(AB) = 0 r(AB)=0 ,故 r ( A ) + r ( B ) ≤ n r(A)+r(B)\le n r(A)+r(B)≤n ,证毕。
结论12
对于 n × n n\times n n×n 矩阵 A A A ,其伴随矩阵的秩
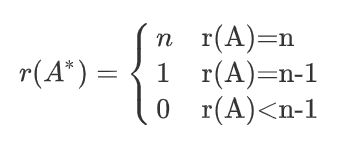
(1) r ( A ) = n ⇒ ∣ A ∣ ≠ 0 ⇒ ∣ A ∗ ∣ = ∣ A ∣ n − 1 ≠ 0 ⇒ r ( A ∗ ) = n r(A)=n \Rightarrow |A| \neq 0 \Rightarrow |A^{*}|=|A|^{n-1} \neq 0 \Rightarrow r(A^{*}) = n r(A)=n⇒∣A∣=0⇒∣A∗∣=∣A∣n−1=0⇒r(A∗)=n .
注: ∣ A ∗ ∣ = ∣ A ∣ n − 1 |A^{*}|=|A|^{n-1} ∣A∗∣=∣A∣n−1 在附录有详细证明,一定不能错过!
(2) r ( A ) = n − 1 ⇒ ∣ A ∣ = 0 ⇒ A A ∗ = ∣ A ∣ E = O ⇒ r ( A ) + r ( A ∗ ) ≤ n ⇒ n − 1 + r ( A ∗ ) ≤ n ⇒ r ( A ∗ ) ≤ 1 r(A)=n-1 \Rightarrow |A|=0 \Rightarrow AA^{*}=|A|E=\bold{O}\Rightarrow r(A)+r(A^{*})\le n\Rightarrow n-1+r(A^{*}) \le n \Rightarrow r(A^{*})\le 1 r(A)=n−1⇒∣A∣=0⇒AA∗=∣A∣E=O⇒r(A)+r(A∗)≤n⇒n−1+r(A∗)≤n⇒r(A∗)≤1
另一方面, r ( A ) = n − 1 ⇒ ∃ n − 1 r(A) =n-1 \Rightarrow \exist n-1 r(A)=n−1⇒∃n−1 阶子式不为0 ⇒ ∃ A i j ≠ 0 ⇒ r ( A ∗ ) ≥ 1 \Rightarrow \exist A_{ij} \ne 0 \Rightarrow r(A^{*}) \ge 1 ⇒∃Aij=0⇒r(A∗)≥1 ,故 r ( A ∗ ) = 1 r(A^{*})=1 r(A∗)=1
(3) r ( A ) < n − 1 ⇒ ∀ n − 1 r(A)
证毕。
习题
题目1:对于 n × n n\times n n×n 的矩阵 A A A ,若 A 2 = A A^{2}=A A2=A ,则 r ( A − E ) + r ( A ) = n r(A-E)+r(A)=n r(A−E)+r(A)=n
证明: A 2 = A ⇒ A ( A − E ) = O ⇒ r ( A ) + r ( A − E ) ≤ n A^{2}=A \Rightarrow A(A-E) = O \Rightarrow r(A)+r(A-E) \le n A2=A⇒A(A−E)=O⇒r(A)+r(A−E)≤n
另一方面, r ( A − E ) + r ( A ) = r ( E − A ) + r ( A ) ≥ r ( E − A + A ) = n r(A-E)+r(A)=r(E-A)+r(A) \ge r(E-A+A)=n r(A−E)+r(A)=r(E−A)+r(A)≥r(E−A+A)=n
故 命题获证
题目2:对于 n × n n\times n n×n 的矩阵 A A A ,若 A 2 = E A^{2}=E A2=E ,则 r ( A − E ) + r ( A + E ) = n r(A-E)+r(A+E)=n r(A−E)+r(A+E)=n
证明: A 2 = E ⇒ ( A + E ) ( A − E ) = O ⇒ r ( A − E ) + r ( A − E ) ≤ n A^{2}=E \Rightarrow (A+E)(A-E)=O \Rightarrow r(A-E)+r(A-E) \le n A2=E⇒(A+E)(A−E)=O⇒r(A−E)+r(A−E)≤n
另一方面, r ( A − E ) + r ( A + E ) = r ( E − A ) + r ( A + E ) ≥ r ( E − A + A + E ) = r ( 2 E ) = n r(A-E)+r(A+E)=r(E-A)+r(A+E) \ge r(E-A+A+E)=r(2E)=n r(A−E)+r(A+E)=r(E−A)+r(A+E)≥r(E−A+A+E)=r(2E)=n 获证。
附录
分块矩阵的初等变换
定义:设分块矩阵 A = ( A i j ) s × t A=(A_{ij})_{s\times t} A=(Aij)s×t,则以下三种变换:
- 交换分块矩阵 A A A 的某两行(列);
- 用一个非奇异矩阵左(右)乘以 A A A 的某一行(列)上;
- 以某一矩阵左(右)乘 A A A 的某一行(列)加到另一行(列)上。
成为分块矩阵 A A A 的行(列)初等变换。将分块矩阵的行、列初等变换统称为分块初等变换。
伴随矩阵
说明:伴随矩阵的定义在此处不在赘述,但是必须提醒大家,伴随矩阵的定义一定要仔细看,很容易搞错的。因为在伴随矩阵中,并不是按照原矩阵元素的位置一一对应放置相应的代数余子式从而构成伴随矩阵。而是把代数余子式按照原矩阵的转置矩阵元素的位置一一对应放置的。
性质1:
A A ∗ = A ∗ A = ∣ A ∣ E AA^{*}=A^{*}A=|A|E AA∗=A∗A=∣A∣E
引理:行列式某一行元素与另一行对应元素代数余子式乘积的和为零。
引理证明:(法1):矩阵某一行的元素和另一行元素的代数余子式相乘时,其实得到的是两行元素相同的行列式。具体地,就是说把另一行的元素强行替换了与代数余子式们对于的那一行的元素。
根据行列式的性质:有两行元素相等时,此行列式为0,故行列式某一行元素与另一行对应元素的代数余子式乘积的和为零。
(法2):在一个矩阵 A A A 中,将第 i i i 行加到第 j j j 行上(行列式值不变),再将行列式按第 j j j 行展开,得
∣ A ∣ = ( a j 1 + a i 1 ) A j 1 + ( a j 2 + a i 2 ) A j 2 + ⋯ + ( a j n + a i n ) A j n = ( a j 1 A j 1 + a j 2 A j 2 + ⋯ + a j n A j n ) + ( a i 1 A j 1 + a i 2 A j 2 + ⋯ + a i n A j n ) = ∣ A ∣ + ( a i 1 A j 1 + a i 2 A j 2 + ⋯ + a i n A j n ) \begin{aligned} |A|&=(a_{j1}+a_{i1})A_{j1}+(a_{j2}+a_{i2})A_{j2}+\dots+(a_{jn}+a_{in})A_{jn} \\ &= (a_{j1}A_{j1}+a_{j2}A_{j2}+\dots+a_{jn}A_{jn})+(a_{i1}A_{j1}+a_{i2}A_{j2}+\dots+a_{in}A_{jn}) \\ &=|A|+(a_{i1}A_{j1}+a_{i2}A_{j2}+\dots+a_{in}A_{jn}) \end{aligned} ∣A∣=(aj1+ai1)Aj1+(aj2+ai2)Aj2+⋯+(ajn+ain)Ajn=(aj1Aj1+aj2Aj2+⋯+ajnAjn)+(ai1Aj1+ai2Aj2+⋯+ainAjn)=∣A∣+(ai1Aj1+ai2Aj2+⋯+ainAjn)
说明:第二个等号是用了 拉普拉斯展开(按行展开)。
故
a i 1 A j 1 + a i 2 A j 2 + ⋯ + a i n A j n = 0 a_{i1}A_{j1}+a_{i2}A_{j2}+\dots+a_{in}A_{jn} = 0 ai1Aj1+ai2Aj2+⋯+ainAjn=0
引理获证。
有了上面的引理,证明上述性质其实是水到渠成的。
证明:
令 A = ( a i j ) n × n A=(a_{ij})_{n\times n} A=(aij)n×n ,根据伴随矩阵定义
A ∗ = ( A 11 A 21 ⋯ A n 1 A 12 A 22 ⋯ A n 2 ⋯ ⋯ ⋯ A 1 n A 2 n ⋯ A n n ) A^{*} = \begin{pmatrix} A_{11} & A_{21}& \cdots &A_{n1}\\ A_{12} & A_{22}& \cdots &A_{n2}\\ \cdots & \cdots & &\cdots \\ A_{1n} & A_{2n}& \cdots &A_{nn}\\ \end{pmatrix} A∗=⎝ ⎛A11A12⋯A1nA21A22⋯A2n⋯⋯⋯An1An2⋯Ann⎠ ⎞
再次提醒,注意看上面伴随矩阵的元素的下角标。
A ∗ A = ( A 11 A 21 ⋯ A n 1 A 12 A 22 ⋯ A n 2 ⋯ ⋯ ⋯ A 1 n A 2 n ⋯ A n n ) × ( a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋯ ⋯ ⋯ a n 1 a n 2 ⋯ a n n ) A^{*}A= \begin{pmatrix} A_{11} & A_{21}& \cdots &A_{n1}\\ A_{12} & A_{22}& \cdots &A_{n2}\\ \cdots & \cdots & &\cdots \\ A_{1n} & A_{2n}& \cdots &A_{nn}\\ \end{pmatrix}\times \begin{pmatrix} a_{11} & a_{12}& \cdots &a_{1n}\\ a_{21} & a_{22}& \cdots &a_{2n}\\ \cdots & \cdots & &\cdots \\ a_{n1} & a_{n2}& \cdots &a_{nn}\\ \end{pmatrix} A∗A=⎝ ⎛A11A12⋯A1nA21A22⋯A2n⋯⋯⋯An1An2⋯Ann⎠ ⎞×⎝ ⎛a11a21⋯an1a12a22⋯an2⋯⋯⋯a1na2n⋯ann⎠ ⎞
没有什么其他技巧,直接矩阵相乘,然后根据上面引理就可以得到,除了主对角线上的元素为 ∣ A ∣ |A| ∣A∣ ,其他地方元素都为 0 0 0 。
A A ∗ = ∣ A ∣ E AA^{*}=|A|E AA∗=∣A∣E
类似可证明。
性质2:若 ∣ A ∣ ≠ 0 |A|\ne 0 ∣A∣=0 则 A ∗ = ∣ A ∣ A − 1 A^{*}=|A|A^{-1} A∗=∣A∣A−1
证明:由性质1,可得
A A ∗ = A ∗ A = ∣ A ∣ E AA^{*}=A^{*}A=|A|E AA∗=A∗A=∣A∣E
由题意, A A A 可逆,且 对 A ∗ A = ∣ A ∣ E A^{*}A=|A|E A∗A=∣A∣E 两边右乘 A − 1 A^{-1} A−1 可得
A ∗ = ∣ A ∣ A − 1 A^{*}=|A|A^{-1} A∗=∣A∣A−1
性质3:若 ∣ A ∣ ≠ 0 |A|\ne 0 ∣A∣=0,则 ∣ A ∗ ∣ = ∣ A ∣ n − 1 |A^{*}|=|A|^{n-1} ∣A∗∣=∣A∣n−1
证明:由性质2,可得
A ∗ = ∣ A ∣ A − 1 A^{*}=|A|A^{-1} A∗=∣A∣A−1
等号两边取行列式得
∣ A ∗ ∣ = ∣ ∣ A ∣ A − 1 ∣ = ∣ A ∣ n ∣ A − 1 ∣ = ∣ A ∣ n ∣ A ∣ − 1 = ∣ A ∣ n − 1 |A^{*}|=||A|A^{-1}|=|A|^{n}|A^{-1}|=|A|^{n}|A|^{-1}=|A|^{n-1} ∣A∗∣=∣∣A∣A−1∣=∣A∣n∣A−1∣=∣A∣n∣A∣−1=∣A∣n−1
实际上,即使 ∣ A ∣ = 0 |A|=0 ∣A∣=0,也有性质3。
若 ∣ A ∣ = 0 |A|=0 ∣A∣=0 由性质1,得 A A ∗ = O AA^{*}=O AA∗=O 故 r ( A ) + r ( A ∗ ) ≤ n r(A)+r(A^{*}) \le n r(A)+r(A∗)≤n
当 r ( A ) = 0 r(A)=0 r(A)=0,即 A = O A=O A=O 时, A ∗ = O A^{*}=O A∗=O , ∣ A ∗ ∣ = ∣ A ∣ n − 1 = 0 |A^{*}|=|A|^{n-1}=0 ∣A∗∣=∣A∣n−1=0
当 r ( A ) ≥ 1 r(A) \ge 1 r(A)≥1 时, 1 ≤ r ( A ) ≤ n − r ( A ∗ ) ⇒ r ( A ∗ ) ≤ n − 1 1 \le r(A) \le n-r(A^{*}) \Rightarrow r(A^{*}) \le n-1 1≤r(A)≤n−r(A∗)⇒r(A∗)≤n−1 ,
即 A ∗ A^{*} A∗ 秩亏, ∣ A ∗ ∣ = 0 |A^{*}| = 0 ∣A∗∣=0 ,从而 ∣ A ∗ ∣ = ∣ A ∣ n − 1 = 0 |A^{*}|=|A|^{n-1}=0 ∣A∗∣=∣A∣n−1=0 。
总结
1.根据结论5,6,得到 r ( A , B ) r(A,B) r(A,B) 的上界是 r ( A ) + r ( B ) r(A)+r(B) r(A)+r(B) ,下界是 m a x { r ( A ) , r ( B ) } , r ( A + B ) max\{r(A),r(B)\},r(A+B) max{r(A),r(B)},r(A+B)。换句话说, r ( A , B ) r(A,B) r(A,B) 可能取到的最大值是 r ( A ) + r ( B ) r(A)+r(B) r(A)+r(B) ,可能取到的最小值是 m a x { r ( A ) , r ( B ) } max\{r(A),r(B)\} max{r(A),r(B)} 或者 r ( A + B ) r(A+B) r(A+B)。
2.根据结论7,10,得到 r ( A B ) r(AB) r(AB) 的上界是 m i n { r ( A ) , r ( B ) } min\{r(A),r(B)\} min{r(A),r(B)} ,下界是 r ( A ) + r ( B ) − n r(A)+r(B)-n r(A)+r(B)−n。换句话说, r ( A B ) r(AB) r(AB) 的可能取到的最大值是 m i n { r ( A ) , r ( B ) } min\{r(A),r(B)\} min{r(A),r(B)} ,可能取到的最小值是 r ( A ) + r ( B ) − n r(A)+r(B)-n r(A)+r(B)−n.
参考文献
[1]董改芳.关于伴随矩阵的性质及应用的研究[J].太原学院学报(自然科学版),2018,36(03):17-19.
[2]殷倩.浅谈矩阵秩的等式与不等式证明[J].数学学习与研究,2018,{4}(15):2-3+7.
[3]智婕.分块矩阵的初等变换[J].甘肃联合大学学报(自然科学版),2011,25(05):22-24.
[4] 行列式某一行元素与另一行对应元素的代数余子式乘积的和为零 是什么意思?