市场经济的物价波动-差分方程模型

1.前言

市场经济中的物价波动是指商品和劳务价格水平在一段时间内持续上升或下降的现象。物价波动的原因有很多，主要包括以下几个方面：

1. 供需关系：当市场上某种商品或劳务的供应量大于需求量时，价格可能下跌；反之，当需求量大于供应量时，价格可能上涨。

2. 生产成本：生产商品或劳务的成本上升可能导致企业提高销售价格。这包括原材料、劳动力、运输等方面的成本。

3. 政府政策：政府的财政政策和货币政策会影响货币供应量和利率水平，从而影响物价。例如，扩张性财政政策可能导致通货膨胀，而紧缩性货币政策可能会抑制通货膨胀。

4. 国际贸易：国际贸易对物价的影响主要表现在汇率变动和国际市场需求变化等方面。汇率升值可能会导致进口商品价格下降，从而拉低国内物价；相反，汇率贬值可能会导致进口商品价格上涨，从而推高国内物价。

5. 预期心理：消费者对未来的预期也会影响物价。如果消费者预期未来物价会上涨，他们可能会提前购买商品，从而导致当前物价上涨；相反，如果消费者预期未来物价会下跌，他们可能会推迟购买，从而导致当前物价下跌。

6. 自然因素：自然灾害、气候变化等自然因素可能影响生产、运输等环节，从而导致物价波动。

物价波动对经济和社会产生重要影响。适度的物价波动有助于资源配置和提高生产效率，但剧烈的物价波动可能导致通货膨胀或通货紧缩，影响经济增长和社会稳定。因此，政府和中央银行通常会采取一定的政策措施来稳定物价。

2.模型假设

当商品的供求关系处于平衡状态时，其数量为,价格为

时间轴制作网站- process on

根据常识我们也知道

供过于求会导致价格下跌

供不应求 会导致价格上升，所以我们假设

代表第k时段商品数量

代表第k时段商品价格

因此我们设想，到底一个什么样的比例系数才能让波动范围不那么大

所以我们根据上面时间轴的对应关系有以下假设

，，……(1)

，，……(2)

(1)带入(2)

  ,……

当k趋于无穷时，可以看出数量x需要保值在平衡范围内的话。

必须小于1，相当于数列极限中的一个公比

小于1，收敛（会趋于确定的某个值，趋于稳定状态）

大于等于1，发散（会趋于无穷，不稳定状态）。

3.模型分析

我们来举个例，假设某种商品在市场上的平衡数量x0=100.y0=10

继续假设开始时段的商品数量x1=110。----，显然他俩乘积小于1.

接下来我们就可以用matlab代码进行可视化处理。

编写mycon.m文件

function [A,X,Y]=mycon(x0,y0,x1)
k=1;
A=ones(10,3);
X=zeros(10,1);
Y=zeros(10,1);
X(1)=x1;
for i=1:10
    Y(k)=-0.1*(X(k)-x0)+y0;
    X(k+1)=5*(Y(k)-y0)+x0;
    k=k+1;
end
t=1:10;
A(:,1)=t';
A(:,2)=X(1:10);
A(:,3)=Y;
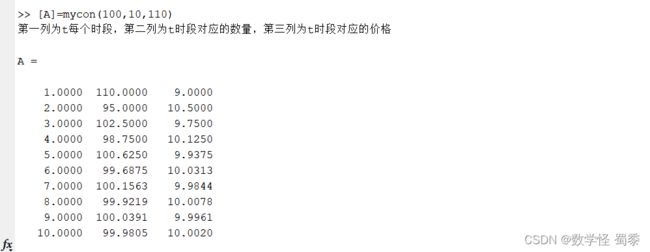
disp('第一列为t每个时段，第二列为t时段对应的数量，第三列为t时段对应的价格')

接着在命令行进行函数调用。得到以下矩阵A. 

 [A]=mycon(100,10,110)

然后进行离散画图处理。 

[A]=mycon(100,10,110)
figure(1)
plot(A(:,1),A(:,2))
xlabel('k')
ylabel('x(k)')
grid on
figure(2)
plot(A(:,1),A(:,3))
xlabel('k')
ylabel('y(k)')
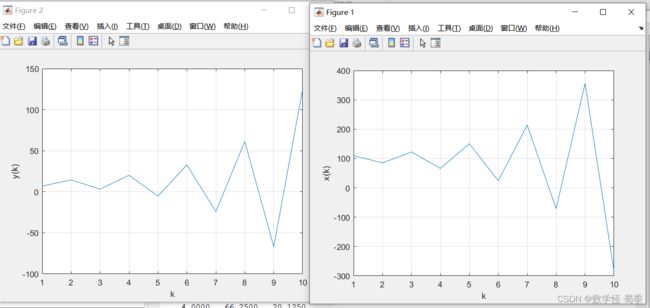
grid on

可以看出，最终会趋于平衡状态。 

当我们把改成0.3 ，=5保持不变.看看会得到什么样的图形

 

 然后还是运行上面的代码

可以发现，商品数量和价格都会趋于不稳定的状态。 

最后得出的结论：

表示消费者的敏感程度，消费者敏感度过高会导致疯狂抢购或者极少抢购，比如疫情期间前期媒体疯狂大肆宣传某些物品会涨价，消费者会大量抢购，市场上的数量就会大量短缺，从而导致价格上升。又比如十几年前搞笑囤盐事件。

表示经营者的敏感程度，经营者敏感度过高会疯狂生产或者极少生产。

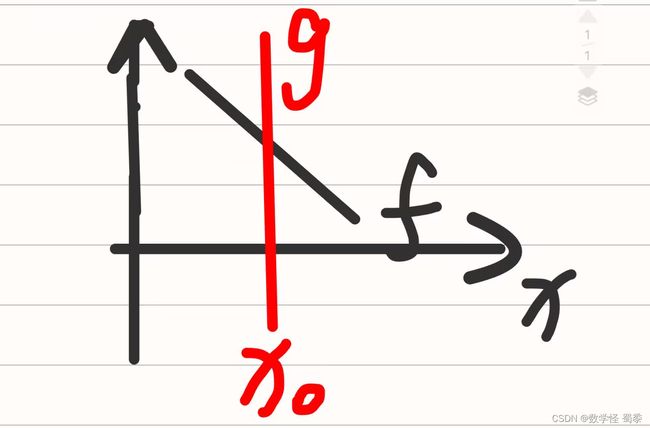
 4.蛛网模型

差分方程模型也可以用经济学的蛛网模型进行直观的解释。

方程（1）表示需求曲线f

方程（2）表示供应曲线g

两条直线方程的交点P0为平衡点。由于种种原因会导致价格和商品数量偏离平衡点。

所以不妨设P1远离平衡点。

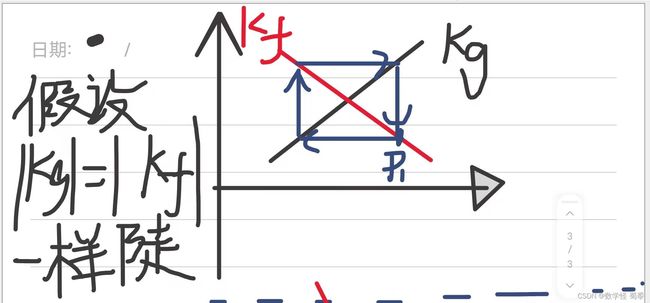
我们来研究g函数不动，f函数变阧或者变平的情况

通过下面图像分析得出结论当f比g平，则会趋于平衡，即，稳定。

 

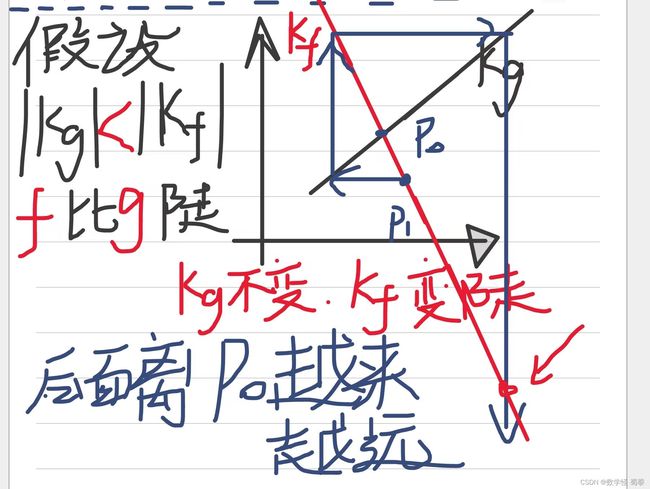
通过下面图像分析得出结论当f比g阧，则会趋于振荡，即,不稳定。

5.政府的干预 

1.使尽量小，如=0，需求曲线f就变为水平

 这是以行政手段控制价格不变

 

2.使尽量小，如=0，需求曲线g就变为水平

这是靠政府的经济实力控制数量不变 

6.模型推广 （新模型）

假设经营者的管理水平和素质提高，根据当前和前一段的价格决定下一时段的产量。即

（3）

把方程（2）改成上面

前面我们已经用原模型算过当

，，，，x0=100,y0=10,x1=110的情况

得到的图像，结果是不稳定的。

随后我们根据上面的新模型进行计算。他就放宽了条件，图像趋于稳定。

那么问题来了，放宽到了多少？这是个问题需要我们研究。

我们把方程（1）带入上面的新模型方程（3），算得以下等式

二阶线性常系数差分方程

易看出该方程的 特解为

特解有了接下来求其通解，则特征方程为

通解为

当时，不稳定（k趋于无穷）（相当于公比不能大于1）。

当时，只有虚根，则

稳定条件

当且仅当

与原模型相比，条件放宽了。

说明提高经营者管理水平和素质还是有利于对经济起到稳定的结果。