【论文阅读】Resource Allocation for Text Semantic Communications
这是一篇关于语义通信中资源分配的论文。全文共5页,篇幅较短。
目录在这里
- 摘要
- 关键字
- 引言
-
- 语义通信
- 资源分配
- 贡献
- 公式符号
- 系统模型
-
- DeepSC Transmitter
- Transmission Model
- DeepSC Receiver
- 语义感知资源分配策略
-
- Semantic Spectral Efficiency (S-SE)
- 问题建模
-
- 优化目标
- 通道分配约束条件
- 平均语义符号数约束条件
- 语义相似度约束条件
- SS-E限制条件
- 解决方法
- 仿真结果
-
- 变换方法
- 基准
- 实验结果
- 结论
摘要
语义通信在传输可靠性方面有着天然优势,而其中的资源分配更是保证语义传输可靠性和通信效率的关键所在,但目前还没有研究者探索该领域。为了填补这一空白,我们研究了语义领域的频谱效率,并重新思考语义感知资源分配问题。具体来说,以文本语义通信为例,首次定义了语义谱效率(S-SE),并用于根据通道分配和传输的语义符号的数量来优化资源分配。此外,为了公平地比较语义通信系统和传统通信系统,开发了一种变换方法,将传统的基于比特的频谱效率转换为S-SE。仿真结果表明了所提出的资源分配方法的有效性和可行性,以及语义通信在S-SE方面的优越性。
关键字
语义通信 语义谱效率 资源分配
引言
语义通信
大家都知道,自从信息革命爆发以来,我们的信息量(数据量)也在不断膨胀。以往当我们进行通信时,是将信息放在信源上,系统就会像快递小哥,发给信宿。

但在这个万物互联的时代,我们的信道已经接近极限,但仍然不足以传输所有数据。这时,语义通信应运而生。
语义通信采用“先理解后发送”的机制,我们不必发送所有信息,仅仅发送最有价值,能够表达意思的信息就可以。
那语义通信怎么工作的呢,或是它的总体架构是怎么样子的。现在,语义通信研究还处于起步阶段,不同的研究团队有着不同的架构设计。而且,针对不同的通信类型(文本通信,音视频通信,图像通信等),语义通信的架构也随之不同。
资源分配
在无线通信中,如何测量信息内容以及频谱效率(SE)是资源分配的基础。我们需要从语义角度重新考虑资源分配。
尽管仍然缺乏完整的数据模型,但借助深度学习(DL)的语义系统设计,可以使得在语义域内定义可计算的SE。在本文中,我们以 DeepSC 为例来探索这种语义感知网络中的 SE 问题和资源分配问题。
贡献
- 针对语义感知网络提出了一种新的资源分配模型。具体来说,首先定义语义谱效率(S-SE)从语义的角度来衡量通信效率。然后提出了一种新的公式,并在信道分配和传输的语义符号的数量方面最大化整体S-SE。
- 为了公平地比较语义通信系统和传统通信系统,开发了一种变换方法将基于比特的SE转换为S-SE。
- 仿真结果验证了所提出的资源分配模型的有效性,以及语义通信系统在S-SE方面的优越性。
公式符号
| 符号 | 含义 |
|---|---|
| R n × m \mathbb{R}^{n\times m} Rn×m | 大小为 n x m 的真实集合 |
| x \mathbf{x} x | 向量 |
| X \mathbf{X} X | 矩阵 |
| x ∼ C N ( μ , σ 2 ) x \sim \mathcal{CN}(\mu, \sigma^2) x∼CN(μ,σ2) | x服从循环对称复高斯分布 |
系统模型
现在考虑如下图所示的蜂窝网络架构1。该架构有一个基站,N个移动站。
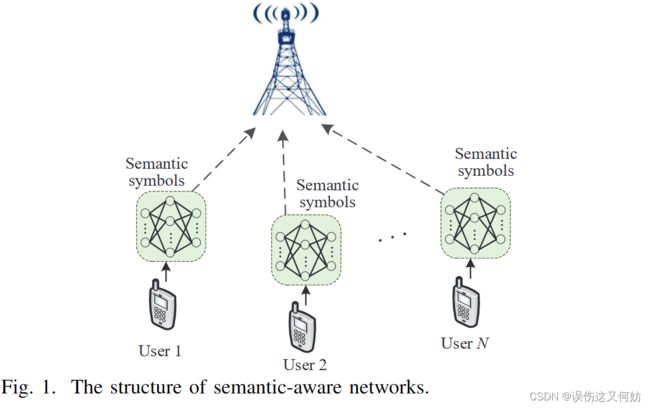
DeepSC 被用作语义通信模型,并配备每个用户进行文本传输,其中底层文本的语义可以通过 Transformer 有效地提取。假设DeepSC收发器在BS或云平台上进行训练。然后将训练好的语义发射机模型广播给用户。下面我们来将详细介绍 BS 处的 DeepSC 发射器、传输模型和 DeepSC 接收器。
DeepSC Transmitter
第n个用户生成文本向量为 s n = [ w n , 1 , w n , 2 , . . . , w n , l , . . . . , w n , L n ] s_n = [w_{n, 1}, w_{n, 2}, ..., w_{n, l}, ...., w_{n, L_n}] sn=[wn,1,wn,2,...,wn,l,....,wn,Ln],向量总长度为 L n L_n Ln。这个向量会被DeepSC Transmitter 映射为Semantic Symbol 向量 X n = [ x n , 1 , x n , 2 , . . . . , x n , k n L n ] X_n = [\mathbf{x_{n, 1}, x_{n, 2}, ...., x_{n, k_nL_n}}] Xn=[xn,1,xn,2,....,xn,knLn]。
其中, X n ∈ R k n L n × 2 X_n \in \mathbb{R}^{k_nL_n\times 2} Xn∈RknLn×2, X n X_n Xn长度会随着 s n s_n sn的增加而增加,在第 n 个用户处,每个单词平均使用 k n k_n kn 个语义符号进行编码,而且每个语义符号可以直接通过传输物质传输。
Transmission Model
| 符号 | 含义 |
|---|---|
| M = { 1 , 2 , . . , m , . . . , M } \mathcal{M}=\{1, 2, .., m, ..., M\} M={1,2,..,m,...,M} | 可用信道集合(带宽为W),M是总数量 |
| α m = [ α n , 1 , . . . , α n , M ] \bm{\alpha_m} = [\alpha_{n, 1}, ..., \alpha_{n, M}] αm=[αn,1,...,αn,M] | 和 第 n 个用户的相关性,只有0 1两个选项 |
| p n p_n pn | 第n个用户的发射功率 |
| g n g_n gn | 大尺度信道增益(包括路径损失和阴影) |
| h n , m h_{n,m} hn,m | 用户 n 在第 m 个信道上的雷利衰落系数 |
| N 0 N_0 N0 | 噪声功率谱密度 |
假设每个信道最多只能分配给一个用户,一个用户至多占据一个信道:
∑ n = 1 N α n , m ≤ 1 \sum^N_{n=1}\alpha_{n, m} \leq 1 n=1∑Nαn,m≤1
∑ m = 1 M α n , m ≤ 1 \sum^M_{m=1}\alpha_{n, m} \leq 1 m=1∑Mαn,m≤1
考虑到信道包含大尺度衰减和小尺度Rayleigh衰减,信噪比(度量用户 n 在第 m 个信道上的信号质量):
γ n , m = p n g n ∣ h n , m 2 ∣ W N 0 \gamma_{n,m}= \frac {p_ {n}g_ {n}|h_ {n,m}^ {2}|}{WN_ {0}} γn,m=WN0pngn∣hn,m2∣
DeepSC Receiver
| 符号 | 含义 |
|---|---|
| Y n = g n h n , m X n + z \bm{Y}_n = \sqrt{g_n}h_{n, m}\bm{X}_n+\mathbf{z} Yn=gnhn,mXn+z | 来自第 n 个用户的信号 |
| s ^ n \widehat {s}_n s n | 估计第 n 个用户的原始向量 |
| B(·) | 来自 Transformers (BERT) 模型的句子双向编码器表示,采用预训练的 Sentence-BERT 模型 |
在 BS 处,来自第 n 个用户的信号可以表示为 Y n Y_n Yn。接收到的信号首先由通道解码器解码,从而语义解码器估计句子 s ^ n \hat{s}_n s^n。为了评估语义通信在文本传输方面的性能,我们采用语义相似度作为性能指标.
ξ = B ( s ) B ( s ^ ) T ∣ B ( s ) ∣ ∣ B ( s ) ∣ \xi = \frac {B(s)B(\widehat {s})^T}{|B(s)||B(s)|} ξ=∣B(s)∣∣B(s)∣B(s)B(s )T
语义感知资源分配策略
S-SE 首先被定义为语义感知网络的新指标。然后语义感知资源分配在通道分配和传输的语义符号的数量方面被表述为 S-SE 最大化问题。最后,得到优化问题的最优解。
Semantic Spectral Efficiency (S-SE)
| 符号 | 含义 |
|---|---|
| D = { ( s j = [ w n , 1 , w n , 2 , . . . , w n , l , . . . . , w n , L n ] ) } j = 1 D \mathcal{D}=\{(s_j=[w_{n, 1}, w_{n, 2}, ..., w_{n, l}, ...., w_{n, L_n}])\}^D_{j=1} D={(sj=[wn,1,wn,2,...,wn,l,....,wn,Ln])}j=1D | 文本数据集,其中 s j s_j sj 是第 j 个句子,长度为 L j L_j Lj, w j , l w_{j,l} wj,l是第 l l l 个单词。 |
| I j I_j Ij | s j s_j sj的语义信息量 |
| p ( s j ) p(\mathbf{s_j}) p(sj) | s j s_j sj 出现概率 |
假设语义信息可以通过表示语义信息基本单元的语义单元 (sut) 来衡量。基于此,可以定义两个关键的基于语义的性能指标:
- 语义传输速率 (S-R) 每秒有效传输的语义信息, 单位suts/s
- 语义谱效率(S-SE) 语义信息可以在带宽单位上成功传输的速率,单位suts/s/Hz
我们关注的是长文本的传输,因此L和I应取期望值,而不是随机值。在第n个用户处,平均有 k n L k_nL knL 个语义符号承载着 I I I 的语义信息量,每个语义符号的平均语义信息量为 I / ( k n L ) I/(k_nL) I/(knL)。
由于符号速率等于通道带宽对于带通传输,在带宽为W的通道上传输的总语义信息量为 W I / ( k n L ) WI/(k_nL) WI/(knL)。(语义信息量和bit数相对应吗),因此,第n个用户在第m个通道上的S-R可以表示为
Γ n , m = W I k n L ξ n , m \Gamma_ {n,m} = \frac {WI}{k_ {n}L} \xi _ {n,m} Γn,m=knLWIξn,m
第n个用户在第m个通道上的SS-E可以表示为
Φ n , m = Γ n , m W = I k n L ξ n , m \Phi _ {n,m} = \frac {\Gamma_ {n,m}}{W} = \frac {I}{k_ {n}L} \xi_{n,m} Φn,m=WΓn,m=knLIξn,m
问题建模
| 符号 | 含义 |
|---|---|
| Φ \Phi Φ | 所有用户整体 S-SE |
信道分配向量是我们优化变量之一。此外,我们还会优化每个单词的传输语义符号的平均数量 k n k_n kn,以使每个符号携带更多的语义信息,从而在确保相同的传输可靠性的同时获得更高的 S-SE。
优化目标
max α n , k n Φ = ∑ n = 1 N ∑ m = 1 M α n , m I k n L ξ n , m \max_{\bm{\alpha_n}, k_n} \Phi=\sum_{n=1}^{N}\sum_{m=1}^M\alpha_{n, m} \frac {I}{k_ {n}L} \xi_{n,m} αn,knmaxΦ=n=1∑Nm=1∑Mαn,mknLIξn,m
通道分配约束条件
-
第 n 个用户是否占用第 m 条信道:
α n , m ∈ { 0 , 1 } \alpha_{n, m} \in \{0, 1\} αn,m∈{0,1} -
每个信道最多只能分配给一个用户:
∑ n = 1 N α n , m ≤ 1 \sum^N_{n=1}\alpha_{n, m} \leq 1 n=1∑Nαn,m≤1 -
一个用户至多占据一个信道:
∑ m = 1 M α n , m ≤ 1 \sum^M_{m=1}\alpha_{n, m} \leq 1 m=1∑Mαn,m≤1
平均语义符号数约束条件
每个单词的平均语义符号数允许范围,K 表示最大值
k n ∈ { 1 , 2 , 3 , . . . , K } k_n\in\{1, 2, 3, ..., K\} kn∈{1,2,3,...,K}
语义相似度约束条件
该约束条件反映所需的最小语义相似度 ξ t h \xi_{th} ξth:
ξ n , m ≥ ξ t h \xi_{n, m} \geq \xi_{th} ξn,m≥ξth
SS-E限制条件
Φ n , m ≥ Φ t h \Phi_{n, m} \geq \Phi_{th} Φn,m≥Φth
解决方法
I / L I/L I/L 对于特定类型的源是一个常数,因此不会影响资源分配优化,目标函数可以改写为:
max α n , k n Φ = ∑ n = 1 N ∑ m = 1 M α n , m ξ n , m k n \max_{\bm{\alpha_n}, k_n} \Phi=\sum_{n=1}^{N}\sum_{m=1}^M\alpha_{n, m} \frac {\xi_{n,m}}{k_ {n}} αn,knmaxΦ=n=1∑Nm=1∑Mαn,mknξn,m
ξ n , m \xi_{n, m} ξn,m 受 特定语义通信系统和物理信道条件的影响,我们在 AWGN 信道上运行 DeepSC 模型,得到了 ξ n , m \xi_{n, m} ξn,m和 ( k n , γ n , m ) (k_n, \gamma_{n, m}) (kn,γn,m) 之间的映射关系。如下图所示:
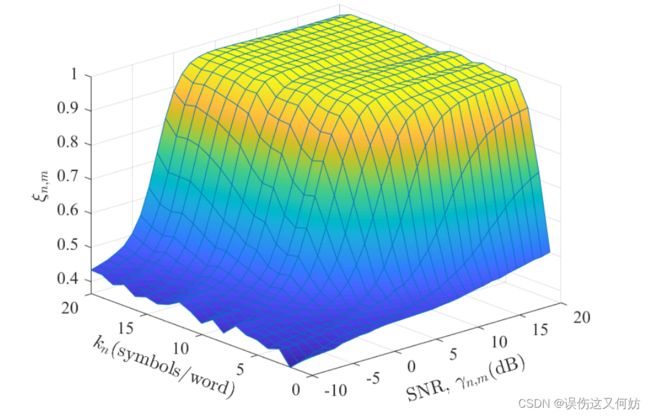
由于不同蜂窝链路的正交性,目标函数可以解耦成下面两个等效的独立优化问题。
- P2 在所有候选通道上为所有用户获取SSE,由于 ξ n , m \xi_{n, m} ξn,m只能通过查表方法获得,因此采用穷尽法求解。
max k n Φ ~ n , m = ξ n , m / k n s . t . C 4 C 5 C 6 \max_{k_n} \tilde{\Phi}_{n, m} = \xi_{n, m}/k_n\\ s.t. \space C_4 \space C_5 \space C_6 knmaxΦ~n,m=ξn,m/kns.t. C4 C5 C6 - P3 可以看作二向图的最大匹配问题。使用匈牙利算法解决。其中两个顶点分布是 N 和 M, Φ ~ n , m m a x \tilde{\Phi}_{n, m}^{max} Φ~n,mmax是第n个用户与第m个通道之间的权重。
max α n ∑ n = 1 N ∑ m = 1 M α n , m Φ ~ n , m m a x s . t . C 1 C 2 C 3 \max_{\bm{\alpha_n}}\sum_{n=1}^{N}\sum_{m=1}^M\alpha_{n, m} \tilde{\Phi}_{n, m}^{max} \\ s.t. \space C_1 \space C_2 \space C_3 αnmaxn=1∑Nm=1∑Mαn,mΦ~n,mmaxs.t. C1 C2 C3
仿真结果
在本节,我们进行了两个实验以全面评估所提出的语义感知资源分配方案的性能。
- 将所提出的资源分配模型与传统的资源分配模型进行比较,以验证语义感知网络中的所提出的模型
- 比较语义通信系统和传统通信系统的S-SE,以显示语义通信的优越性
由于传统系统通常在 bit 域中进行评估,我们开发了一种变换方法,将SE 转换成 S-SE ,从而实现公平比较。
变换方法
| 符号 | 含义 |
|---|---|
| C n , m C_{n, m} Cn,m | 第n用户第m信道的传输速率 bits/s |
| μ \mu μ | 转换因子,每个单词的平均比特数 bits/word |
在传统通信系统中, 单词中的每个字母都可以通过源编码器映射到bit。从语义通信角度来看,每个位都可以简单地认为是一个语义符号。因此,等效S-R可以表示为:
Γ n , m ′ = C n , m I μ L ξ n , m \Gamma_{n, m}^{'}=C_{n, m}\frac{I}{\mu L}\xi_{n, m} Γn,m′=Cn,mμLIξn,m
我们假设传统通信中没有位误差时, ξ n , m \xi_{n,m} ξn,m等于1。等效S-SE可以表示为:
Φ n , m ′ = R n , m I μ L \Phi_{n, m}^{'} = R_{n, m}\frac{I}{\mu L} Φn,m′=Rn,mμLI
基准
本文所提出的资源分配方案是针对特定的语义系统,即DeepSC。我们将和下面三个基准进行比较:
- 理想系统:信道可以达到香农极限,且无比特误差。
- 4G 系统
- 5G 系统
实验结果
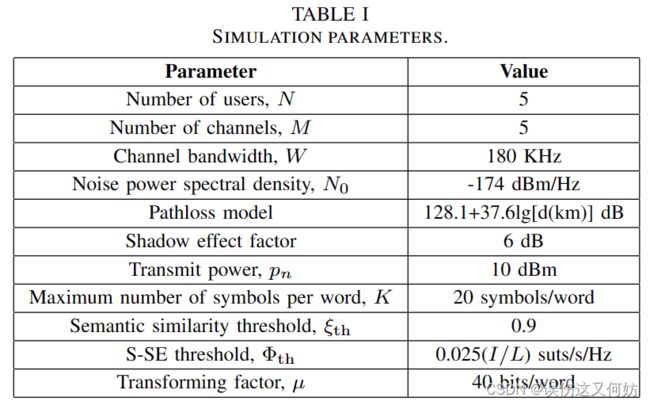
在我们的模拟中,考虑了半径为 r = 500 m 的圆形网络,其中 N 个用户均匀分布。除非另有说明,相关参数列于表 I。
我们首先检查了语义感知网络中的传统资源分配模型。在该仿真中,将理想系统中传统模型的最优信道分配结果以及不同的 k n k_n kn值。然后将得到的 S-SE 与所提出的模型进行比较。如图 3 所示,无论 kn 的值如何,传统模型的 SSE 都小于所提出模型的 SSE,这意味着传统模型不适合语义感知网络。此外, k n k_n kn = 3 的传统模型的 S-SE 等于 0,因为在这种情况下语义相似性小于阈值。
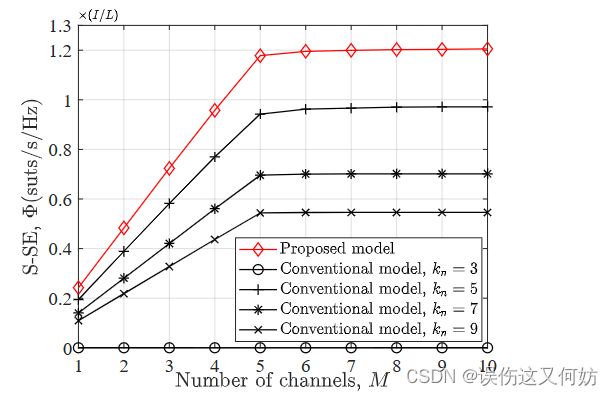
下面,我们将不同的通信系统与相应的资源分配模型进行比较。
-
不同系统的 S-SE 与通道数的关系
当 M 从 1 增加到 5 时,所有系统的 S-SE 都会迅速增加,因为服务更多用户。然后当 M 继续从 5 增加到 10 时,S-SE 增长缓慢而不是保持稳定,因为有更多的通道可用,用户可以选择具有更高 SNR 的通道。
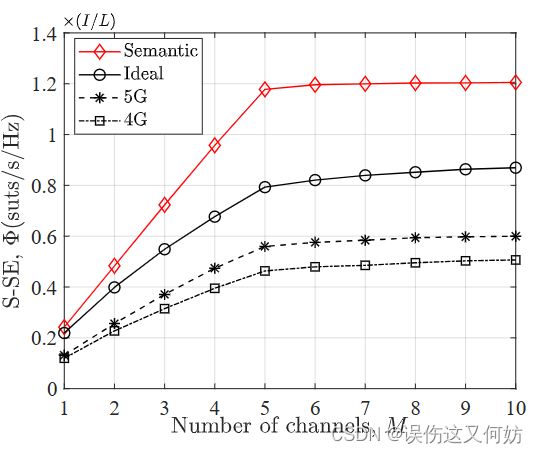
-
S-SE与发射功率的关系
随着pn的增加,理想系统的S-SE迅速增加,而语义通信系统、4G系统和5G系统的S-SE先增大后趋于常数,这意味着所有实际系统都具有信噪比增加的上界。此外,语义通信系统由于其压缩数据的能力更强,比 4G 和 5G 具有更大的上限。

-
S-SE 与转换因子的关系
语义通信系统的性能保持稳定,因为转换因子与其无关。对于传统系统,S-SE 随着 μ 的增加而减小,因为 S-SE 是 SE 与 μ 的比率,最大 SE 是不同 μ 的固定值。此外,当 μ 大于 19 位/字时,语义通信系统的性能优于 4G 和 5G。然而,当μ小于大约27位/字时,即一个词可以编码为小于27位,语义通信系统的性能比理想系统差。该图表明,语义通信系统是否大大优于传统系统中采用的源编码方案。

结论
在本文中,我们研究了语义域中的 SE 问题,并探索了语义通信的资源分配。具体来说,首先定义了 S-R 和 S-SE,以便基于 DeepSC 模型测量语义通信系统的通信效率。为了最大化所有用户的整体SSE,语义感知资源分配被表述为一个优化问题,得到了最优解。
我们也进行了广泛的模拟以评估所提出方案的性能。对于文本传输,当单词通过传统的源编码技术平均映射到超过 19 位时,语义通信系统实现了比 4G 和 5G 系统更高的 S-SE。此外,如果编码单词所需的位增加到超过 27 位,发射功率为 10 dBm,语义通信系统甚至优于理想系统。
未来,如何设计资源分配方法来满足包括单模态和多模态任务在内的多个智能任务的要求,应该进一步研究。
【1】https://www.eet-china.com/mp/a245114.html
https://zh.wikipedia.org/wiki/%E8%9C%82%E7%AA%9D%E7%BD%91%E7%BB%9C# ↩︎