最长回文子串

如果一个字符串正着读和倒着读是一样的，我们则称它是回文字符串。给定一个长度为N的字符串S，求它的最长回文子串。$N\le 1000$。

1.枚举回文串中心位置，利用字符串Hash比较相等

我们可以枚举S的回文子串的中心位置i=1~N，看从这个中心位置出发左右两侧最长可以扩展出多长的回文串。也就是说：

1.求一个最大整数x使得$S[i-x+1\sim i]=reverse(S[i\sim i+x-1])$，那么以i为中心的最长奇回文子串长度为$2\ast x-1$。

2.求一个最大整数y使得$S[i-y\sim i-1]=reverse(S[i\sim i+y-1])$，那么以i为中心的最长偶回文子串长度为$2\ast x$。

我们$O(N)$预处理Hash值后，可以$O(1)$计算任意子串的Hash值。我们还可以对x和y的值进行二分答案，用Hash值$O(1)$比较一个正着读和一个逆着读的子串是否相等，从而在$O(logN)$的时间里求出x和y的值。时间复杂度为$O(NlogN)$。

#include 
using namespace std;

string s;
unsigned long long f1[1005],f2[1005],p[1005];

int main()
{
    cin>>s;
    int n=s.size();
    s=' '+s;
    p[0]=1;
    for(int i=1;i<=n;++i)
    {
        f1[i]=f1[i-1]*131+s[i];
        p[i]=p[i-1]*131;
    }
    for(int i=n;i>=1;--i)
        f2[i]=f2[i+1]*131+s[i];
    int cnt=0;
    int pos1=0,pos2=0;
    int x=0,y=0;
    for(int i=1;i<=n;++i)
    {
        int l=x,r=min(i,n-i+1);
        while(l<=r)
        {
            int m=(l+r)/2;
            if(f1[i]-f1[i-m]*p[m]==f2[i]-f2[i+m]*p[m])
            {
                l=m+1;
                x=m;
            }
            else
                r=m-1;
        }
        if(2*x-1>cnt)
        {
            cnt=2*x-1;
            pos1=i-x+1,pos2=i+x-1;
        }
        l=y,r=min(i-1,n-i+1);
        while(l<=r)
        {
            int m=(l+r)/2;
            if(f1[i-1]-f1[i-1-m]*p[m]==f2[i]-f2[i+m]*p[m])
            {
                l=m+1;
                y=m;
            }
            else
                r=m-1;
        }
        if(2*y>cnt)
        {
            cnt=2*y;
            pos1=i-y,pos2=i+y-1;
        }
    }
    for(int i=pos1;i<=pos2;++i)
        printf("%c",s[i]);
    return 0;
}

2.Manacher算法

Manacher（又称马拉车）算法用于解决求最长回文串的问题，它能在$O(n)$的线性时间复杂度里解决问题。

首先为了解决奇回文串和偶回文串的问题，在每个字符间插入“#”，并且为了使的扩展过程中，到边界自动结束，在两端分别插入“^”和“$”，两个不可能出现在字符串中的字符，在中心扩展时，判断两端字符是否相等时，如果到了边界一定不相等，从而跳出循环。经过处理，字符串的长度永远都是奇数了。

我们用一个数组P保存从中心扩展的最大个数，而它刚好是去掉“#”的原字符串的总长度。用P的下标i减去P[i]，然后再除以2，就是原字符串的开头下标了。

例如我们找到P[i]的最大值为5，也就是回文串的最大长度是5，对应下标是6，所以原字符串的开头下标是(6-5)/2=0。所以我们只需要返回原字符串第0到第(5-1)位就可以了。

求每个P[i]是这个算法的关键，它充分利用了回文串的对称性。

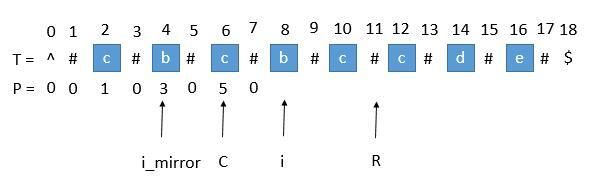
我们用$C$表示回文串的中心，$R$表示回文串的右边半径坐标，所以$R=P[C]+C$。$C$和$R$所对应的回文串是当前循环中R最靠右的回文串。用$i\_mirror$表示当前需要求的第$i$个字符关于$C$对称的下标：

我们要求$P[i]$，如果是用中心拓展法，那就向两边拓展对比就行了。但是其实我们可以利用回文串C的对称性。$i$关于$C$的对称点为$i\_mirror$，$P[i\_mirror]=3$，所以$P[i]=3$。

但有三种情况将会造成直接赋值$P[i\_mirror]$是错的。

1.超出了R

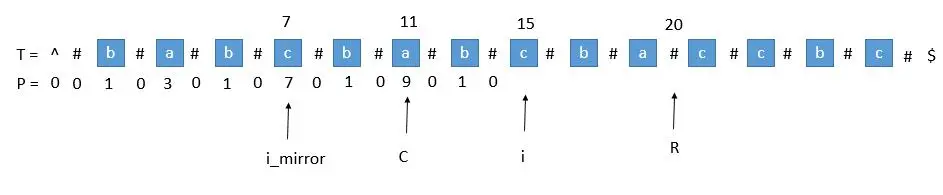
当我们要求$P[i]$的时候，$P[mirror]=7$，而此时 $P[i]$并不等于 7 ，为什么呢，因为我们从 i 开始往后数 7 个，等于 22 ，已经超过了最右的 R ，此时不能利用对称性了，但我们一定可以扩展到 R 的，所以 $P[i]$ 至少等于 $R-i=20-15=5$，会不会更大呢，我们只需要比较$T[R+1]$和$T[R+1]$关于 i 的对称点就行了，就像中心扩展法一样一个个扩展。

2.$P[i\_mirror]$遇到了原字符串的左边界

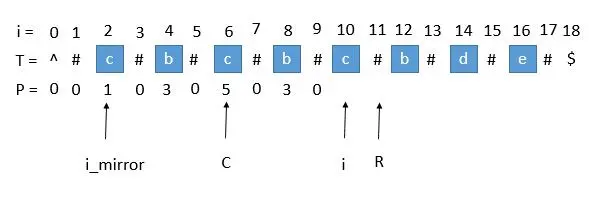
此时$P[i\_mirror]=1$，但是 $P[i]$ 赋值成 1 是不正确的，出现这种情况的原因是 $P[i\_mirror]$在扩展的时候首先是 “#” == “#” ，之后遇到了 "^"和另一个字符比较，也就是到了边界，才终止循环的。而$P[i]$并没有遇到边界，所以我们可以继续通过中心扩展法一步一步向两边扩展就行了。

3.$i$大于等于$R$

此时我们先把$P[i]$ 赋值为 0 ，然后通过中心扩展法一步一步扩展就行了。

就这样一步一步的求出每个 $P[i]$，当求出的 $P[i]$ 的右边界大于当前的 R 时，我们就需要更新 C 和 R 为当前的回文串了。因为我们必须保证 i 在 R 里面，所以一旦有更右边的 R 就要更新 R。

#include 
using namespace std;

int P[2050];
int cnt,ans;

string preProcess(string s)
{
    string s_pro="^";
    for(int i=0;i<s.size();++i)
        s_pro+='#',s_pro+=s[i];
    s_pro+='#',s_pro+='$';
    return s_pro;
}

void Manacher(string s)
{
    string t=preProcess(s);
    int n=t.size();
    int c=0,r=0;
    for(int i=1;i<n-1;++i)
    {
        int j=2*c-i;
        if(r>i)
            P[i]=min(r-i,P[j]);
        else
            P[i]=0;
        while(t[i+P[i]+1]==t[i-P[i]-1])
            P[i]++;
        if(P[i]+i>r)
        {
            r=P[i]+i;
            c=i;
        }
        if(P[i]>cnt)
        {
            cnt=P[i];
            ans=i;
        }
    }
}

int main()
{
    string s;
    cin>>s;
    Manacher(s);
    for(int i=(ans-P[ans])/2;i<(ans-P[ans])/2+cnt;++i)
        printf("%c",s[i]);
    return 0;
}