《Learning Fine-grained Features via a CNN Tree for Large-scale Classification》阅读笔记
论文标题
《Learning Fine-grained Features via a CNN Tree for Large-scale Classification》
通过 CNN 树学习细粒度特征,实现大规模分类
作者
Zhenhua Wang,Xingxing Wang,Gang Wang
以色列耶路撒冷希伯来大学计算机科学与工程学院
新加坡南洋理工大学电气与电子工程学院
阿里巴巴人工智能实验室,杭州,中国
初读
摘要
- 我们提出了一种增强卷积神经网络(CNN)可区分性的新方法。其主要思路是建立一个树状结构,通过只学习这些类别中的特征,逐步学习细粒度特征,以区分类别子集。
- 与针对所有类别学习的特征相比,这些特征有望更具区分性。
- 我们开发了一种新算法,可以有效地从大量类别中学习树形结构。大规模图像分类任务的实验证明,我们的方法可以提高给定基本 CNN 模型的性能。我们的方法非常通用,因此有可能与许多其他深度学习模型结合使用。
结论
- 本文提出了一种 CNN 树,用于逐步学习细粒度特征,以区分被基本 CNN 模型混淆的类别子集。
- 与针对所有类别学习的特征相比,这些特征有望更具区分性。因此,被基本 CNN 模型误分类的测试示例可能会被底层的特定 CNN 模型正确分类。
- 为了学习树状结构和细粒度特征,我们提出了一种新的学习算法,以自上而下广度优先的方式生长树状结构。
- 使用 AlexNet 和 GoogleNet 进行的大规模图像分类任务实验表明,我们的方法可以提高给定基本 CNN 模型的可辨别性。所提出的方法相当通用,因此有可能与许多其他深度学习模型结合使用。
再读
Section 1 Introduction
- 第一段:单 CNN 模型现状
- 卷积神经网络(CNN)最近在许多任务中表现出卓越的性能,如图像分类、物体检测、物体跟踪、文本检测、文本识别、局部特征描述、视频分类、人体姿态估计、场景识别和场景标记。
- 在经典的 CNN 框架中,CNN 会针对所有类别学习 7 个共享特征层(5 个卷积层和 2 个全连接层),然后由最后一个全连接层根据所学特征区分不同类别。这些学习到的特征编码了具有区分性的视觉模式,对分类非常有用。
- 不过,**对于不同的类别子集,视觉判别模式应该有所不同。**例如,用于区分猫和狗的特征应该与用于区分草和树的特征不同。
- 在当前的 CNN 模型中,我们只是针对不同的类别子集,将不同类型的判别特征融合到一个模型中。那么对于某个类别子集来说,学习到的用于区分其他类别的特征可能会成为噪音。因此,由于缺乏足够的表示能力,这种单一的 CNN 模型可能不是理想的分类方法。
- 第二段:针对一个类别子集学习细粒度特征
- 在本文中,我们提出了一种新方法来增强 CNN 在大规模多类分类中的可辨别性。其关键思路是专门针对一个类别子集学习细粒度特征。与针对所有类别学习的特征相比,这种细粒度特征有望更好地捕捉子集类别的视觉模式。
- 理想情况下,对于一个类别 c i c_i ci,如果我们能识别出混淆集 S i S_i Si,它包含了所有可能的类别,其测试示例可能会被基本 CNN 模型分类为 c i c_i ci,那么我们就可以只针对这个混淆集 S i S_i Si 学习特定的 CNN 模型。
- 由于 S i S_i Si 包含的类别比整个类别集少,因此特定 CNN 模型应编码对该混淆集更有用的辨别视觉模式。这样,被基本 CNN 模型误判为 c i c_i ci 的测试示例就可能被特定 CNN 模型纠正。
- 第三段:计算成本高
- 当类别数量较多时(如 1000 个),为每个类别学习一个特定的 CNN 模型的计算成本会很高。
- 更糟糕的是,在这种情况下,可能很难在测试过程中将所有 CNN 模型缓存到内存中。这样一来,测试速度就会大大降低,因为我们必须频繁地从硬盘加载模型。
- 因此,我们需要开发先进的方法来减少需要训练的特定 CNN 模型的数量。
- 第四段:合并混淆集
- 我们观察到,有些类别的混淆集有许多共同的类别。那么,我们可以通过合并混淆集,为这些类别训练一个共享的 CNN 模型。
- 我们可能会牺牲准确性,因为现在我们的特定 CNN 模型要处理更多的类别,但与此同时,我们可以减少需要训练的特定 CNN 模型的数量。
- 我们可以反复重复这一过程:给定新的 CNN 模型,重新估计该模型中每个类别的混淆集,然后分别为每个混淆集训练一个特定的 CNN 模型。最后,我们将建立一棵 CNN 模型树,每个模型只针对若干类别学习判别特征。
- 第五段:合并混淆集的权衡
- 在合并混淆集时,我们应该在效率和准确性之间做出权衡。
- 我们提出的优化问题是,最大限度地减少合并混淆集的数量,同时要求生成的 CNN 模型的错误率低于某个阈值。
- 这一目标难以实现。因此,我们通过限制每个合并集中的类别数量来放宽对准确性的限制。这个分配问题类似于虚拟机打包问题,是一个 NP 难问题。而且可能不存在好的多时间近似算法。
- 本文提出了一种基于直觉的启发式算法,即重叠较多的混淆集应优先合并在一起,以优化集间类别共享的效益。
- 第六段:评估
- 为了评估所提出的方法,我们使用 AlexNet 和 GoogleNet 作为基本 CNN 模型。
- 在 ILSVRC 2015 数据集上的实验表明,我们的方法可以提高这两个模型的性能。这充分证明了所提方法的有效性。
- 我们的方法非常通用,因此有可能与许多其他深度学习模型结合使用。
本文接下来的内容安排如下: 第 2 节概述了相关工作。第 3 节介绍了一种新型 CNN 树,并详细描述了树学习算法。第 4 节进行了实验评估,最后我们在第 5 节对本文进行总结。
Section 2 Related Work
-
卷积神经网络在计算机视觉领域有着悠久的历史。
- 自 LeCun 等人提出以来,它在识别任务中一直与其他方法竞争。最近,随着大规模类别级训练数据(如 ImageNet)的出现,卷积神经网络在大规模视觉识别中表现出了卓越的性能。
- 最值得注意的是,Krizhevsky 等人提出了一种经典的 CNN 架构,该架构包含 8 个学习层(5 个卷积层和 3 个全连接层),在图像分类任务上比以前的方法有了显著的改进。
-
人们提出了多种技术来提高 CNN 在不同方面的性能。
所有这些方法都是从整个类集中学习通用特征,而这些特征可能对特定子集中的类没有区分度。与此不同的是,我们的方法是针对树中的每个类子集逐步学习细粒度特征。与在整个类集中学习的通用特征相比,这些特征在区分特定类子集方面应该更有辨别力。
-
Hinton 等人提出了一种名为 "Dropout "的方法,以防止在训练数据上出现复杂的协同适应。这种方法只是在每个训练案例中省略一半的特征检测器,因此一个隐藏单元不能依赖于其他隐藏单元的存在。
-
Wan 等人推出的 DropConnect 是 Dropout 的换代产品,用于规范神经网络中的大型全连接层。与 Dropout 不同的是,DropConnect 将网络中随机选择的权重子集设置为零。这样,每个单元都从上一层的随机单元子集接收输入。
-
Ciresan 等人提出了一种多列 CNN,通过将多个 CNN 列组合在一起来提高性能。
-
Goodfellow 等人提出了一种名为 Maxout 的新模型,旨在促进 Dropout 的优化并提高 Dropout 快速近似模型平均技术的准确性。
-
Howard 提出了一些新的有用的图像转换方法,以增加训练集的有效大小并生成更多的测试预测。他们还展示了一种训练更高分辨率模型的有效方法,可生成有用的补充预测。
-
Wu 等人还提出了更复杂的模型训练数据增强技术。
-
He 等人提出了一种名为 SPP-net 的新网络结构,它为 CNN 配备了一种更原则性的池化策略,即 “空间金字塔池化”。SPP 网可以生成固定长度的表示,而不受图像大小的影响。此外,由于使用了金字塔池,它对物体变形也具有很强的鲁棒性。
-
Ioffe 等人提出了一种名为 "批量归一化 "的方法,通过对每个训练小批量进行归一化处理来减少内部协变量的偏移。这种方法允许训练程序使用更高的学习率,对初始化的要求也更低,在某些情况下还无需使用 Dropout。
-
Zeiler 和 Fergus 提出了一种新颖的可视化方法,可以让人深入了解中间特征层的功能和分类器的运行情况,并展示了如何利用这些可视化方法找出模型的问题,从而获得更好的性能。只需减小层滤波器大小和卷积步长,他们就能显著提高性能。
-
Simonyan 和 Zisserman 研究了 CNN 深度对其大规模图像分类准确性的影响。他们的研究表明,表示深度有利于提高分类精度。
-
Szegedy 等人提出了一种新的 CNN 架构,通过增加网络的深度和宽度实现了高性能。
-
He 等人引入了一种残差学习框架来简化网络的训练。他们的网络比现有的所有作品都要深得多,并实现了最先进的性能。
-
-
与我们的工作相关的另一种方法是分层分类法。许多论文都提出要利用对象类别之间的层次结构。
然而,在这些方法中,在顶层被错误分类的测试示例无法在后面恢复。相比之下,我们的方法能够恢复被基本模型误分类的测试示例,因为它可以学习细粒度特征来区分混淆集。
-
Griffin 和 Perona 提出了一种自动构建分类树的算法。
-
Deng 等人和 Torralba 等人提出利用 WordNet 的语义层次结构来改进分类。
-
Bengio 等人提出了一种用于大规模分类的标签嵌入树。它将类别递归地划分为不相交的子集,并为每个子集训练一个分类器。
-
Deng 等人通过同时确定树结构和学习树中每个节点的分类器,改进了标签树。他们还允许不同子集之间的重叠。这些分层方法的主要目的是加快测试操作速度。
-
Section 3 The Proposed CNN Tree
拟议的 CNN 树
3.1 Overview
-
针对不同混淆集逐步学习细粒度特征:
我们发现,在多类分类中,一个类通常会被其他几个类混淆。在本文中,我们将它们称为该类的混淆集。基于这一观察结果,我们开发了一种针对不同混淆集逐步学习细粒度特征的方法。
-
方法概述:
假定 C ~ \tilde{\mathcal{C}} C~ 是多类分类任务的整个类集 M ~ \tilde{M} M~ 是 C ~ \tilde{\mathcal{C}} C~ 上学习的基本 CNN 模型。类 c i c_i ci 的混淆集 S i \mathcal{S}_i Si 是一个包含 c i c_i ci 和所有其他类的集合,这些类的测试示例有可能被 M ~ \tilde{M} M~ 误判为 c i c_i ci。在类的数量较多的情况下,我们基于一个类只应被整个类集中的少数类似类混淆的直觉,声称 ∣ S i ∣ ≪ ∣ C ~ ∣ |\mathcal{S}_i|\ll|\tilde{\mathcal{C}}| ∣Si∣≪∣C~∣。这为进一步提 M ~ \tilde{M} M~ 的准确性提供了有价值的信息。具体来说,我们可以训练一个特定的 CNN 模型,只学习每个 S i \mathcal{S}_i Si 的细粒度特征。由于 S i \mathcal{S}_i Si 包含的类别较少,这些细粒度特征应该比 M ~ \tilde{M} M~ 在 C ~ \tilde{\mathcal{C}} C~ 上学习到的通用特征更具区分度。当一个测试示例 M ~ \tilde{M} M~ 分类为 c i c_i ci 时,我们就可以使用在 S i \mathcal{S}_i Si 上训练的特定 CNN 模型来完善其类别标签。我们希望,被基本 CNN 模型误分类的测试示例可能会被新的特定 CNN 模型正确分类。
-
此方法的局限性:
然而,在处理大量类别时,为每个类别分别学习特定的 CNN 模型的计算成本非常高昂。在测试过程中,也很难在内存中缓存所有的 CNN 模型,从而导致测试速度大大降低。为了缓解这一问题,我们采用了一种树形结构来逐步学习细粒度特征,即 CNN 树。
-
在正式介绍拟议的 CNN 树之前,我们在表 1 中总结了一些术语,以方便理解。
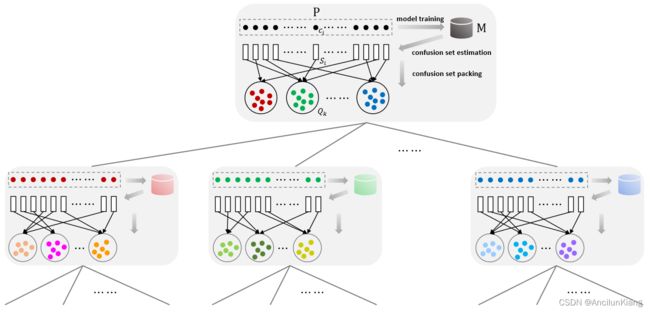
图片注解:CNN 树的学习过程。给定树中的一个节点,我们首先对其类集进行模型训练。接着,我们使用训练好的模型估算每个类别的混淆集。然后将这些混淆集打包成若干混淆超集,并将每个混淆超集分配给一个新的子节点,以便进一步学习。这个过程不断重复,直到达到最大深度。
-
CNN 树构建过程概述:
假设 T = ( V , E ) T=(V, E) T=(V,E) 是一棵 CNN 树。如图 1 所示,对于节点 v ∈ V v\in V v∈V,我们会得到一个类别子集 P ( v ) ⊂ C ~ \mathcal{P}(v)\subset\tilde{\mathcal{C}} P(v)⊂C~。我们尝试通过在 P ( v ) \mathcal{P}(v) P(v) 上学习特定的 CNN 模型 M ( v ) M(v) M(v) 来对 P ( v ) \mathcal{P}(v) P(v) 中的不同类别进行分类。如果 v v v 不是叶节点,我们需要进一步提高 M ( v ) M(v) M(v) 的可区分性。为此,我们使用第 3.2.1 节中描述的方法,基于 M ( v ) M(v) M(v) 重新估计每个 c i ∈ P ( v ) c_i\in\mathcal{P}(v) ci∈P(v) 的混淆集 S i \mathcal{S}_i Si。根据观察,一些类别的混淆集可能有很多共同的类别,我们可以将它们打包成一个混淆超集,即取它们的联合,以减少需要训练的 CNN 数量。在混淆集打包过程中,一个混淆集只能打包成一个超集。**假设合并后得到 N N N 个混淆超集,将分别生成 N N N 个子节点。**设 ϕ ( v ) ⊂ V \phi(v)\subset V ϕ(v)⊂V 为节点 v v v 的子节点集。对于子节点 u k ∈ ϕ ( v ) u_k\in\phi(v) uk∈ϕ(v),混淆超集 Q k \mathcal{Q}_k Qk 被分配给类子集 P ( u k ) \mathcal{P}(u_k) P(uk) ,以便在 Q k \mathcal{Q}_k Qk 上进一步学习特定的 CNN 模型。
-
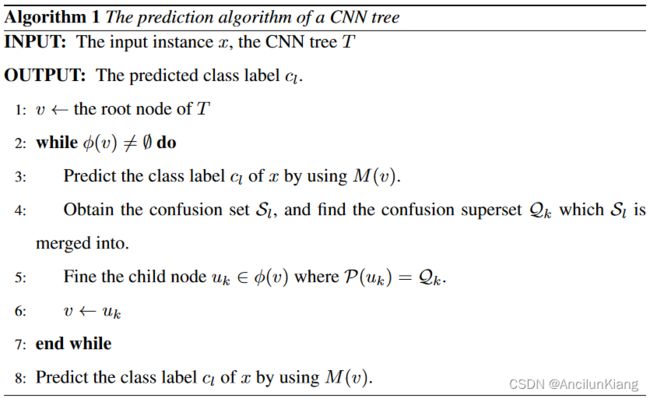
CNN 树预测过程概述:
使用构建的 CNN 树对输入实例 x x x 进行分类时,我们使用算法 1 中所示的预测算法。具体来说,我们从根节 v ~ \tilde{v} v~ 开始,用 M ( v ~ ) M(\tilde{v}) M(v~) 预测 x x x 的类别标签 c l c_l cl。为了确定细化预测的子节点,我们会得到 c l c_l cl 的混淆集 S l \mathcal{S}_l Sl,并找到 S l \mathcal{S}_l Sl 被合并到的混淆超集 Q k \mathcal{Q}_k Qk。然后,我们转到 P ( u k ) = Q k \mathcal{P}(u_k )=\mathcal{Q}_k P(uk)=Qk 的子节点 u k u_k uk。请注意,所选的子节点是唯一的,因为在训练过程中,混淆集 S l \mathcal{S}_l Sl 被唯一地合并为一个混淆超集。在子节点 u k u_k uk,我们可以使用在 P ( u k ) \mathcal{P}(u_k ) P(uk) 上学习到的特定 CNN 模型 M ( u k ) M(u_k) M(uk) 来完善预测。这一过程不断重复,直到到达叶节点。该叶节点的特定 CNN 模型预测的类别标签被视为最终结果。
-
特点:
值得注意的是,本文提出的方法与分层分类法有很大不同。分层分类法的主要目的是加快测试操作速度。这些方法将类别递归地划分为不同的子集,并为每个子集训练一个分类器。然而,在这些方法中,在顶层被错误分类的测试实例无法在后面恢复。相比之下,我们的方法通过在混淆集上逐步学习更具体的模型来完善基本模型预测的类别标签。由于特定模型可以学习细粒度特征来区分混淆的类别,因此它能够纠正被基本模型误分类的测试示例。
3.2 Learning CNN Tree
学习型 CNN 树
学习 CNN 树 T = ( V , E ) T=(V, E) T=(V,E) 指的是学习树结构以及每个节点的特定 CNN 模型。对于每个非叶节点,我们提出了一个软最大混淆矩阵来稳健地估计该节点上的类混淆集,并开发了一种启发式算法来有效地将它们合并为多个混淆超集。对于每个非根节点,我们展示了如何学习特定的 CNN 模型来区分该节点上的类别。
3.2.1 Confusion Set Estimation
混淆集估计
-
常规混淆矩阵法:
给定 CNN 树的非叶 v v v,我们需要估计每个 c i ∈ P ( v ) c_i\in\mathcal{P}(v) ci∈P(v) 的混淆集。我们根据混淆矩阵进行估计。**混淆矩阵是评估多类分类算法性能的常用方法,它将实际类标签与预测类标签进行对比。**具体来说, n n n 类问题的混淆矩阵是一个 n × n n\times n n×n 矩阵 H H H,其中第 i j ij ij 个条目 h i j h_{ij} hij 代表 c i c_i ci 类的测试实例被预测为属于 c j c_j cj 类的百分比。一些研究人员已经提出了基于混淆矩阵探索类别间关系的方法。这些算法的性能主要取决于使用保留验证数据集计算出的混淆矩阵的准确性。然而,对于大规模多类分类问题,收集足够大的验证数据集来计算混淆矩阵以准确测量类间关系是不切实际的。例如,ILSVRC 2015 数据集提供的验证数据集每类只有 50 个样本。由于总共有 1000 个不同的类,在如此小的验证数据集上计算出的混淆矩阵无法充分捕捉所有这些类之间的关系。对于丰富的训练数据,不适合使用它们来直接计算基于分类结果的混淆矩阵,因为模型将拟合训练数据,无法在其上生成有意义的混淆矩阵。
-
软最大混淆矩阵
-
思想:
为了解决上述问题,我们提出了一种可利用丰富训练数据的混淆矩阵变体。我们注意到,CNN 中 softmax 层的输出代表了输入实例对所有类别的预测置信度得分。这些分数确实捕捉到了不同类别之间的混淆信息,并且更能抵御过度拟合。因此,通过对所有训练数据的预测置信度得分求和,就可以合理地获得所有类别间混淆信息的稳健估计。我们将这种变量称为软最大混淆矩阵。
-
详述:
对于非叶节点 v v v,假设有 n v n_v nv 个类别(即 ∣ P ( v ) ∣ = n v |\mathcal{P}(v)|=n_v ∣P(v)∣=nv),类别 c i c_i ci 有 t i t_i ti 个训练实例。假设 x i k x_{ik} xik 是 c i c_i ci 的第 k k k 个训练实例, p i k p_{ik} pik 是当前 CNN 模型 M ( v ) M(v) M(v) 的 softmax 层针对 x i k x_{ik} xik 的 n v n_v nv 维输出向量。那么,软最大混淆矩 H ~ \tilde{H} H~ 的计算公式为:
H ~ = [ h ~ 1 T h ~ 2 T ⋮ h ~ n v T ] \tilde{H}= \begin{bmatrix} \tilde{h}^T_1\\ \tilde{h}^T_2\\ \vdots\\ \tilde{h}^T_{n_v} \end{bmatrix} H~= h~1Th~2T⋮h~nvT
其中
h ~ i = 1 t i ∑ k = 1 t i p i k \tilde{h}_i=\frac{1}{t_i}\sum^{t_i}_{k=1}p_{ik} h~i=ti1k=1∑tipik
根据上述定义, H ~ \tilde{H} H~ 的第 i j ij ij 个条目 h i j h_{ij} hij 衡量了 c i c_i ci 的例子在当前模型 M ( v ) M(v) M(v)上被归类为 c j c_j cj 的可能性。考虑到第 j j j 列 h ~ ⋅ , j \tilde{h}_{\cdot,j} h~⋅,j,它由所有分数组成,用来衡量在 M ( v ) M(v) M(v) 上相应类别的示例被归类为 c j c_j cj 的可能性有多大。给定一个合适的阈值 α \alpha α,只保留大于 α \alpha α 的条目的类别标签,就可以从 h ~ ⋅ , j \tilde{h}_{\cdot,j} h~⋅,j 中导出一个集合 S j \mathcal{S}_j Sj。由于 S j \mathcal{S}_j Sj 包含可能被 c j c_j cj 混淆的类别,即最有可能被预测为 c j c_j cj 的类别,因此我们将其视为对 c j c_j cj 混淆集的估计。图 2 显示了 ILSVRC 2015 训练数据集中一些类别的示例图像,以及利用 AlexNet 的 softmax 混淆矩阵估算出的它们的混淆集。可以看出,每个类别都与其混淆类别有一些相似之处(如外观、形状、大小等)。要将它们从混淆类中区分出来,还需要更具体的特征。
-
图片注解:在 ILSVRC 2015 数据集上使用基本 CNN 的 softmax 混淆矩阵获得的某些类别的示例图像及其相应的混淆集。请注意,不同类别可能有不同数量的混淆类。
3.2.2. Confusion Set Packing
混淆集包装
-
混淆集包装思想:
给定一个非叶节点 v v v 和通过使用 M ( v ) M(v) M(v) 的软最大混淆矩阵估算出的 P ( v ) \mathcal{P}(v) P(v) 中每个类别的混淆集,我们将把这些混淆集合并为多个混淆超集。我们可能会牺牲准确性,因为现在我们的特定 CNN 模型要处理更多的类别,但与此同时,我们可以减少需要训练的 CNN 模型的数量。我们的目标是尽可能减少混淆超集的数量,但每个超集的 CNN 模型的错误率必须较低。但是,我们无法尝试所有组合,找出在此约束条件下混淆超集数量最少的组合。相反,我们将这一约束条件改为限制每个混淆超集中的类别数量。这是基于这样一个假设,即 CNN 的性能与其旨在区分的类别数量密切相关。
-
混淆集包装详述:
-
相似于垃圾箱打包问题:
让 Q \mathcal{Q} Q 表示混淆超集。在 ∣ Q ∣ |\mathcal{Q}| ∣Q∣ 的给定极限 L L L 下,最优解是使生成的 Q \mathcal{Q} Q 数量最小的解。这个问题类似于已被广泛研究的垃圾箱打包问题,其目的是将不同体积的物体以最小化所用垃圾箱数量的方式打包到具有极限体积的有限数量的垃圾箱中。
-
公式化描述:
给定 n n n 个候选超集 B i , i ∈ { 1 , … , n } \mathcal{B}_i, i\in\{1,\dots, n\} Bi,i∈{1,…,n} 以及所有 n n n 个类别的混淆集 S i , i ∈ { 1 , … , n } \mathcal{S}_i, i\in\{1,\dots, n\} Si,i∈{1,…,n} ,混淆集打包问题可表述为:
最小化
N = ∑ i = 1 n y i N=\sum^n_{i=1}y_i N=i=1∑nyi
从属于
∣ ⋃ j = 1 n S i j ^ ∣ ≤ y i L , ∀ i ∈ { 1 , … , n } ∑ i = 1 n ∣ S i j ^ ∣ = ∣ S i ∣ , ∀ j ∈ { 1 , … , n } \begin{align} \left|\bigcup^n_{j=1}\hat{\mathcal{S}_{ij}}\right|\le y_iL,\forall i\in\{1,\dots,n\}\\ \sum^n_{i=1}\left|\hat{\mathcal{S}_{ij}}\right|=\left|\mathcal{S}_i\right|,\forall j\in\{1,\dots,n\} \end{align} j=1⋃nSij^ ≤yiL,∀i∈{1,…,n}i=1∑n Sij^ =∣Si∣,∀j∈{1,…,n}
其中
y i = { 1 i f B i i s u s e d 0 o t h e r w i s e ∀ i ∈ { 1 , … , n } \begin{equation} y_i=\left\{ \begin{aligned} & 1 && if\ \mathcal{B}_i\ is\ used\\ & 0 && otherwise \end{aligned} \quad\right.\forall i\in\{1,\dots,n\} \end{equation} yi={10if Bi is usedotherwise∀i∈{1,…,n}S ^ i j = { S j i f S i i s p a c k d i n t o B i ∅ o t h e r w i s e ∀ i , j ∈ { 1 , … , n } \begin{equation} \hat{\mathcal{S}}_{ij}=\left\{ \begin{aligned} & \mathcal{S}_j && if\ \mathcal{S}_i\ is\ packd\ into\ \mathcal{B}_i\\ & \varnothing && otherwise \end{aligned} \quad\right.\forall i,j\in\{1,\dots,n\} \end{equation} S^ij={Sj∅if Si is packd into Biotherwise∀i,j∈{1,…,n}
需要注意的是,公式 4 中的第一个约束条件确保了混淆超集的大小限制,而第二个约束条件则确保了一个混淆集只能被打包到一个混淆超集中一次。
给定问题的解,N 个混淆超集 Q k \mathcal{Q}_k Qk, k ∈ { 1 , … , N } k\in\{1,\dots, N \} k∈{1,…,N},可通过以下方法求得:
Q k = { ⋃ S j ∣ S ^ i k j ≠ ∅ , j = 1 , 2 , … , n } , ∀ y i k = 1 \mathcal{Q}_k=\left\{\bigcup\mathcal{S}_j|\hat{\mathcal{S}}_{i_kj}\ne\varnothing,j=1,2,\dots,n\right\},\forall y_{i_k}=1 Qk={⋃Sj∣S^ikj=∅,j=1,2,…,n},∀yik=1
-
-
与传统的垃圾箱打包问题的不同点:
与传统的垃圾箱打包问题不同,由于重叠的原因,多个混淆集的累积大小可以小于单个混淆集的大小之和,即 ∣ ⋃ j = 1 n S i j ^ ∣ ≤ ∑ i = 1 n ∣ S i j ^ ∣ \left|\bigcup^n_{j=1}\hat{\mathcal{S}_{ij}}\right|\le\sum^n_{i=1}\left|\hat{\mathcal{S}_{ij}}\right| ⋃j=1nSij^ ≤∑i=1n Sij^ 。实际上,混淆集打包问题是一个虚拟机打包问题,具有一般共享模型,如文献[31]所述,不同的虚拟机打包到物理服务器时可以共享空间。要找到这样一个问题的最优解非常困难,因为它的计算复杂度为 NP-hard。文献[31]表明,要得到一个近似解甚至是不可行的。
-
启发式算法:
在此,我们提出了一种启发式算法,该算法基于这样一种直觉,即重叠度较高的混淆集应优先打包在一起,以优化集间共享的效益。该算法通过将一个混淆集分别分配给一个超集来初始化 n n n 个混淆超集。每一步,算法都会在所有可能的超集对中贪婪地寻找重叠度最大的超集对,这些超集对的联合集不超过混淆超集的大小限制,然后将它们合并在一起。具体算法见算法 2。
3.2.3. Learning Specific CNN Model
特定学习的 CNN 模型
给定一个非根节点 v v v 和一个类子集 P ( v ) \mathcal{P}(v) P(v),我们将只为这个子集学习一个特定的 CNN 模型。
设 v ′ v′ v′ 为 v v v 的父节点, ∣ P ( v ) ∣ = n v |\mathcal{P}(v)|=n_v ∣P(v)∣=nv。我们通过在 P ( v ) \mathcal{P}(v) P(v) 上微调 v ′ v′ v′ 的 CNN 模型,即 M ( v ′ ) M(v′) M(v′) 来学习 M ( v ) M(v) M(v)。这样,我们仍然可以利用更多类别的视觉知识。具体来说,我们遵循 [6] 中描述的程序。**首先,我们移除 M ( v ′ ) M(v′) M(v′) 的最后一个全连接层。接着,我们添加一个新的随机初始化全连接层,该层有 n v n_v nv 个输出单元。**然后,我们运行随机梯度下降法(SGD),在 P ( v ) \mathcal{P}(v) P(v) 的训练数据上学习新的 CNN 模型。由于 CNN 可以同时学习卷积特征和分类权重,因此微调过程应能编码出更具区分性的视觉模式,从而更有力地区分 P ( v ) \mathcal{P}(v) P(v) 中的类别。
3.2.4. Summary
总结
我们在算法 3 中总结了学习 CNN 树的算法。
- 首先用整个类集 C ~ \tilde{\mathcal{C}} C~ 和给定的基本 CNN 模型 M ~ \tilde{M} M~ 初始化根节点 v v v。
- 然后执行递归过程,以自上而下广度优先的方式生长树,直到达到给定的最大深度。
- 随着树的生长,我们可以学习特定的 CNN 模型,每个模型只针对若干类别学习细粒度特征。
Section 4 Experiments
4.1 Dataset and The Evaluation Criteria
数据集和评估标准
-
数据集:
我们利用 ILSVRC 2015 数据集对所提出的方法进行了图像分类任务评估。
- 该数据集包含从 Imagenet 层次结构中选出的 1000 个叶节点类别。
- 其中约有 120 万张图像用于训练,5 万张图像用于验证,每张图像都与一个基本真实类别相关联。
- 按照之前的论文,我们在验证数据上测试我们的方法。我们使用两个标准来评估算法:
- top-1 错误率(将第一个预测的类别标签与地面实况进行比较)
- 和 top-5 错误率(检查地面实况是否属于前 5 个预测的类别标签)。
-
模型选择:
-
我们使用 AlexNet 和 GoogleNet 作为基本 CNN 模型。为了进行公平比较,我们使用了 Caffe 实现,并下载了 ILSVRC 2015 数据集的预训练模型。
-
构建 CNN 树的参数是:
- 树的最大深度 D D D,
- 以及混淆超集的大小极限 L d L_d Ld,级别 d ∈ { 0 , 1 , … , D − 1 } d\in\{0,1,\dots,D-1\} d∈{0,1,…,D−1}.
-
我们测试了在 AlexNet 上使用不同参数的效果。
-
对于 50 50 50、 100 100 100、 150 150 150 和 200 200 200 的 L 1 L_1 L1,表 2 列出了 top-1(top-5)的误差。可以发现,不同的设置会带来相似的性能。
- 图片注解:使用 1 个 AlexNet 作为基本模型时,不同 L 1 L_1 L1 值的 Top-1 和 Top-5 错误率
-
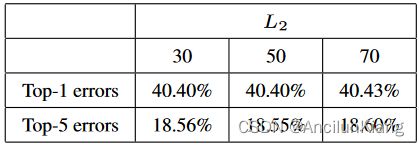
将 L 1 L_1 L1 设置为 100 100 100, L 2 L_2 L2 设置为 30 30 30、 50 50 50 和 70 70 70 时,误差 top-1(top-5)如表 3 所示。性能也相似。
- 图片注解:使用 1 个 AlexNet 作为基本模型并将 L 1 L_1 L1 设置为 100 100 100 时,不同 L 2 L_2 L2 值的 Top-1 和 Top-5 错误率
-
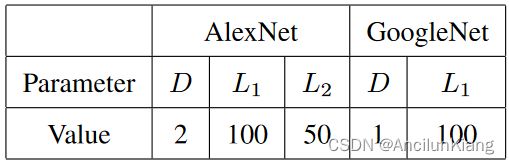
实际上,我们并没有在验证集上优化参数。我们根据经验选择了表 4 所示的参数,因为它们对性能影响不大。
- 图片注解:CNN 树的选定参数
-
请注意,我们为 AlexNet 和 GoogleNet 选择的 D D D 值分别为 2 2 2 和 1 1 1,因为更深的树需要训练更多的 CNN,但这只会带来性能的小幅提升。
-
-
4.2 Results
-
CNN 树与基本 CNN 模型对比
首先,我们将不同深度的 CNN 树与基本 CNN 模型进行比较。我们使用 AlexNet 和 GoogleNet 作为基本模型,因为它们是广泛使用的代表性架构。我们将深度为 D D D 的 CNN 树称为 T D T_D TD(注意, T 0 T_0 T0 是基本 CNN 模型)。
-
表 5 和表 6 分别汇总了 AlexNet 和 GoogleNet 在 ILSVRC 2015 上的结果(基本模型数为 1 1 1 的一列)。
-
使用 AlexNet 在 2015 年 ILSVRC 验证数据上不同数量基本模型的 Top-1 和 Top-5 错误率。基本模型表示为 T 0 T_0 T0。深度为 D = 1 D=1 D=1 和 D = 2 D=2 D=2 的 CNN 树分别记为 T 1 T_1 T1 和 T 2 T_2 T2。括号中的分数是与 T 0 T_0 T0 相比减少的误差。
-
使用 GoogleNet 在 ILSVRC 2015 验证数据上不同基本模型的 Top-1 和 Top-5 错误率。基本模型表示为 T 0 T_0 T0 深度为 D = 1 D=1 D=1 的 CNN 树表示为 T 1 T_1 T1。括号中的分数是与 T 0 T_0 T0 相比减少的误差。
-
-
结果分析:
- 对于 AlexNet, T 1 T_1 T1 与 T 0 T_0 T0 相比,top-1 错误率降低了 2.41 % 2.41\% 2.41%,top-5 错误率降低了 1.43 % 1.43\% 1.43%。当深度增加到 2 2 2 时, T 2 T_2 T2 使 top-1 错误率降低了 2.69 % 2.69\% 2.69%,top-5 错误率降低了 1.49 % 1.49\% 1.49%。
- 对于 GoogleNet, T 1 T_1 T1 可将 top-1 错误率降低 4.38 % 4.38\% 4.38%,top-5 错误率降低 1.91 % 1.91\% 1.91%。由于 GoogleNet 的任务是将 50,000 个示例分为 1,000 个不同的类别,因此这些改进尤其显著。
- 结果表明,所提出的 CNN 树可以增强基本 CNN 的可区分性。其原因可以解释为,特定的 CNN 模型可以学习更多的判别特征来区分混淆的类别。有人可能会说,增加深度和宽度也能提高标准 CNN 的性能。通过比较 AlexNet 和 GoogleNet 的结果,我们注意到我们的方法在提高强大的基本模型(如 GoogleNet)的性能方面更胜一筹。这可能是因为强基本模型估计的混淆集比弱基本模型估计的混淆集更准确。这意味着我们的方法可以享受优化单一基本模型的好处。在实践中,我们可以将 CNN 树与优化后的基本模型相结合,以进一步提高性能。
-
-
对多个基本模型的改善:
由于单个模型的性能总能通过多个模型的平均值得到改善,因此我们接着研究了所提出的方法是否也能改善多个基本模型。我们首先通过不同的随机初始化训练多个基本 CNN 模型,然后为每个基本模型训练一棵 CNN 树。最终预测结果由不同基本模型的 CNN 树的预测结果平均得出。
- AlexNet 和 GoogleNext 的结果也分别如表 5 和表 6 所示。
- 同上表 5 和表 6
- 结果分析:
- 将 AlexNet 的 6 个基本模型平均后, top-1(top-5)误差从 43.09% (20.04%) 降至 39.63% (17.43%),而在这 6 个基本模型上应用我们的 CNN 树后, top-1(top-5)误差进一步降至 37.19% (16.23%)。
- 另一方面,对 GoogleNet 的 6 个基本模型进行平均处理后, top-1(top-5)误差从 32.75% (12.00%) 降至 29.56% (10.08%),而应用我们的 CNN 树后, top-1(top-5)误差进一步降至 25.15% (8.12%)。
- 可以看出,将 CNN 树应用于多个基本模型可以进一步提高性能,这可能是因为多个基本模型估计的混淆集比单一基本模型估计的混淆集更稳健,有助于纠正更多的误分类样本。这也表明,所提出的方法提供了超越模型平均化的价值。
- AlexNet 和 GoogleNext 的结果也分别如表 5 和表 6 所示。
-
模型平均化时模型数量的影响:
-
实验结果
-
结果分析:
- 图三:
- 对于 AlexNet,平均 16 个模型会将 top-1(top-5)误差减小到 39.15 % 39.15\% 39.15%( 16.99 % 16.99\% 16.99%)。
- 对于 GoogleNet,平均 12 个模型可将 top-1(top-5)误差减小到 29.29 % 29.29\% 29.29%( 9.76 % 9.76\% 9.76%)。
- 可以看出,模型平均只能在一定程度上降低误差率,使用更多的模型并不能进一步降低误差率。但是,如果将我们的方法与模型平均相结合,即在平均后的基本模型上应用所提出的 CNN 树,错误率就会显著降低。这充分证明了我们的方法比模型平均法更有价值。
- 表七:
- 对于 AlexNet,在不学习特征的情况下进行微调,top-1 的错误率降低了 0.13 % 0.13\% 0.13%,top-5 的错误率甚至增加了 0.1 % 0.1\% 0.1%。
- 对于 GoogleNet,不进行特征学习的微调会使 top-1 和 top-5 的错误率分别降低 0.59 % 0.59\% 0.59% 和 0.25 % 0.25\% 0.25%。
- 这一策略的表现远不如通过特征学习对特定 CNN 模型进行微调。这表明,所提出的 CNN 树通过逐步学习每个类子集的细粒度特征,增强了可区分性。
- 图三:
-
-
CNN 树的纠正特性:
-
图 4 给出了使用 AlexNet 对验证数据中某些类别的 top-1 预测结果。每幅图像都标有两个标签,其中顶部标签由基本 CNN 模型预测,底部标签由建议的 CNN 树预测。红色表示预测正确,绿色表示预测错误。
图片注解:验证数据上某些类别的 top-1 预测。每张图像都标记有两个标签,顶部标签由基本 CNN 模型预测,底部标签使用提出的 CNN 树预测。红色(绿色)表示与 Ground Truth 相比,预测是错误的(正确的)。
-
结果分析:
可以看出,我们的方法可以纠正一些被基本 CNN 模型错误分类的例子。这是因为我们的方法可以通过在混淆集上逐步学习更具体的模型来完善基本模型预测的类别标签。
-
4.3 Computational Complexity Analysis
计算复杂度分析
-
模型数量:
使用表 4 中的参数设置(4.1 节)
- 对于 AlexNet,我们实际上在 l e v e l 1 level\ 1 level 1 微调了 55 55 55 个特定的CNN模型,每个模型包含不超过 100 100 100 个类,在 l e v e l 2 level\ 2 level 2 微调了 151 151 151 个特定的 CNN 模型,每个模型包含不超过 50 50 50 个类。
- 对于 GoogleNet,我们在 l e v e l 1 level\ 1 level 1 微调了 61 61 61 个特定的 CNN 模型,每个模型也包含不超过 100 100 100 个类。
-
训练细节:
为了微调这些模型,我们从 0.001 0.001 0.001 的学习率开始 SGD(初始预训练率的 1 / 10 1/10 1/10),当验证数据的准确性停止提高时,学习率降低 10 10 10 倍。
-
时间消耗:
- 对于 AlexNet,在 l e v e l 1 level\ 1 level 1 中,每个CNN模型在大约 15000 15000 15000 次迭代后停止学习,在 l e v e l 2 level\ 2 level 2 中大约 5000 5000 5000 次迭代后停止学习。因此,学习这样的 CNN 树总共需要大约 150 150 150 万次迭代,这是学习基本模型( 31 31 31 万次迭代)的 5 5 5 倍。
- 在实验中,我们在 12 12 12 个 Tesla K40 GPU 上并行训练所提出的 CNN 树。完成训练过程大约需要 1.5 1.5 1.5 天。
- 对于测试,我们的方法将时间增加了 2 2 2 倍,因为每个测试示例需要由 3 3 3 个CNN进行评估。对于 GoogleNet,在 l e v e l 1 level\ 1 level 1 中,每个 CNN 模型在大约 80000 80000 80000 次迭代后停止学习。因此,它总共需要大约 480 480 480 万次迭代,这是学习基本模型( 240 240 240 万次迭代)的 2 2 2 倍。在相同的平台上完成训练过程大约需要 2 2 2 天。由于树深度为 1 1 1,因此测试时间增加了 1 1 1 倍。