力扣热题100道-双指针篇
文章目录
-
- 双指针
-
- 283.移动零
- 11.盛最多水的容器
- 15.三数之和
- 42.接雨水
双指针
283.移动零
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
示例 1:
输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]
示例 2:
输入: nums = [0]
输出: [0]
/*
思路:双指针算法
将不等于0的挪到前面,后面全部补为0
*/
class Solution {
public:
void moveZeroes(vector<int>& nums) {
int i=0,j=0;
for(auto c:nums){
if(c!=0){
nums[j++]=c;
}
}
for(j;j<nums.size();j++) nums[j] = 0;
}
};
11.盛最多水的容器
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明:你不能倾斜容器。
示例 1:
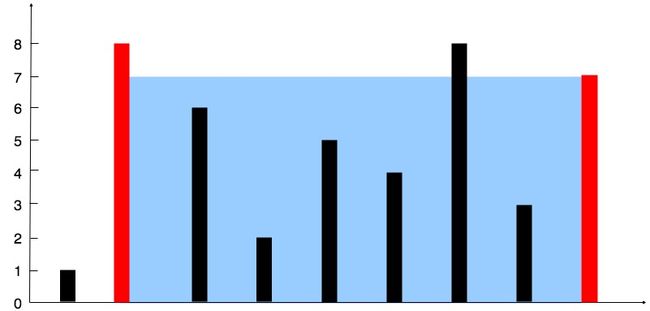
输入:[1,8,6,2,5,4,8,3,7]
输出:49
解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例 2:
输入:height = [1,1]
输出:1
/*
思路 左右往里面夹着,每次以最低的为高,算个面积 一直算直到两者相等,求出最高即可
//先将i往里挪 还是先将j往里挪呢? 注意是先挪低的那一方
在每个状态下,无论长板或短板向中间收窄一格,都会导致水槽 底边宽度 −1 变短:
若向内 移动短板 ,水槽的短板 min(h[i],h[j]) 可能变大,因此下个水槽的面积 可能增大 。
若向内 移动长板 ,水槽的短板 min(h[i],h[j]) 不变或变小,因此下个水槽的面积 一定变小 。
*/
class Solution {
public:
int maxArea(vector<int>& height) {
int i=0,j=height.size()-1;
int res = 0;
while(i<j){
int min = height[i]<height[j]?height[i]:height[j];
//先将i往里挪 还是先将j往里挪呢? 先挪低的
res = max(min*(j-i),res);
if(height[i]<height[j]) i++;
else j--;
}
return res;
}
};
15.三数之和
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请
你返回所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例 1:
输入:nums = [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
解释:
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意,输出的顺序和三元组的顺序并不重要。
示例 2:
输入:nums = [0,1,1]
输出:[]
解释:唯一可能的三元组和不为 0 。
示例 3:
输入:nums = [0,0,0]
输出:[[0,0,0]]
解释:唯一可能的三元组和为 0 。
/*
思路:
先对数组进行排序 三指针 i j k,固定i j往右增大 k往左缩小
主要设置去除重复值,前面出现的不用去除 如 -1 -1 2, -2 1 1 遇到第一个重复的可能会用到后面的值不用去重,后面重复的需要去除
*/
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
sort(nums.begin(),nums.end());
vector<vector<int>>res;
for(int i=0;i<nums.size();i++){
//将i固定
if(i&&nums[i] == nums[i-1]) continue;
for(int j=i+1,k=nums.size()-1;j<k;j++){
if(j>i+1 && nums[j] == nums[j-1]) continue;
while(j<k && nums[i]+nums[j]+nums[k]>0) k--;
if(j<k && nums[i]+nums[j]+nums[k] == 0)
res.push_back({nums[i],nums[j],nums[k]});
}
}
return res;
}
};
42.接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:
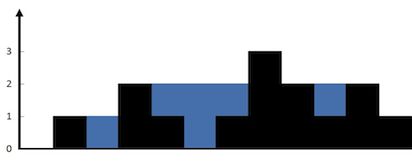
输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
输入:height = [4,2,0,3,2,5]
输出:9
/*
实现思路 //针对除第一个和最后一个柱子 找左边最大的右边最大的 的最小值(包括本身) -当前高度
*/
class Solution {
public:
int trap(vector<int>& height) {
//针对除第一个和最后一个柱子 找左边最大的右边最大的(包括本身)-当前高度
int n = height.size();
vector<int> left(n),right(n);
left[0]=height[0],right[n-1] = height[n-1];
for(int i=1;i<height.size();i++){
left[i] = max(left[i-1],height[i]);
right[n-i-1] = max(right[n-i],height[n-i-1]);
}
int res = 0;
for(int i=1;i<n-1;i++){
res += min(left[i],right[i]) - height[i];
}
return res;
}
};