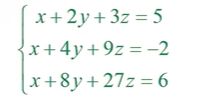matlab-矩阵
矩阵的建立
1、将矩阵元素用中括号括起来,同一行元素用逗号隔开,不同行元素用分号隔开。
>> A = [1,2,3;4,5,6;7,8,9]
A =
1 2 3
4 5 6
7 8 9
2、利用已建好的矩阵建立更大的矩阵,一个大矩阵可以由已经建立好的小矩阵拼接而成。
>> A = [1,2,3;4,5,6;7,8,9];
>> B = [-1,-2,-3;-4,-5,-6;-7,-8,-9];
>> C = [A,B,B,A]
C =
1 至 6 列
1 2 3 -1 -2 -3
4 5 6 -4 -5 -6
7 8 9 -7 -8 -9
7 至 12 列
-1 -2 -3 1 2 3
-4 -5 -6 4 5 6
-7 -8 -9 7 8 9
3、用实部矩阵和虚部矩阵构建复数矩阵
>> A = [1,2,3;4,5,6];
>> B = [7,8,9;3,2,1];
>> C = A+B*i
C =
1.0000 + 7.0000i 2.0000 + 8.0000i 3.0000 + 9.0000i
4.0000 + 3.0000i 5.0000 + 2.0000i 6.0000 + 1.0000i
结构矩阵
格式:结构矩阵元素.成员名 = 表达式
>> %结构矩阵:矩阵元素有3个name,age,grade
>> D(1).name = 'zhangsan';D(1).age = '18';D(1).grade = 90;
>> D(2).name = 'lisi';D(2).age = '18';D(2).grade = 80;
>> D(3).name = 'wangwu';D(3).age = '20';D(3).grade = 85;
单元矩阵
建立单元矩阵与一般矩阵类似,单元矩阵需要用大括号将元素括起来。
>>b = {'zhangsan', '18' ,90;'lisi', '18', 80; 'wangwu','20', 85}
b =
3×3 cell 数组
{'zhangsan'} {'18'} {[90]}
{'lisi' } {'18'} {[80]}
{'wangwu' } {'20'} {[85]}
矩阵元素的引用
1、通过下标引用:A(3,2) = 100
若下标超出矩阵的范围,则将自动扩展矩阵,并会将扩展后没有赋值的元素位置设为0```
>> A = [1,2,3;4,5,6];
>> A(4,5) = 100
A =
1 2 3 0 0
4 5 6 0 0
0 0 0 0 0
0 0 0 0 100
2、通过序号引用
在matlab中,矩阵元素的存储是按照列存储的。
>> A = [1,2,3;4,5,6];
>> A(4,5) = 100
A =
1 2 3 0 0
4 5 6 0 0
0 0 0 0 0
0 0 0 0 100
>> A(5)
ans =
2
1、通用的特殊矩阵
【1】零矩阵:zeros函数
【2】1矩阵:ones函数
【3】单位矩阵:eye函数
【4】随机矩阵:rand函数-产生(0,1)区间的均匀分布随机矩阵。fix(a+(b-a+1)*×):产生la,b]区间上均匀分布的随机整数。
【5】randn:产生均值为0,方差为1的标准正态分布矩阵。u十σ×:得到均值为u、方差σ^2为的随机数。
>> B = zeros(5,5)
B =
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
>> B = zeros(5,7)
B =
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
>> B = ones(5,5)
B =
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
>> B = eye(3,3)
B =
1 0 0
0 1 0
0 0 1
>> B = rand(4,3)
B =
0.8147 0.6324 0.9575
0.9058 0.0975 0.9649
0.1270 0.2785 0.1576
0.9134 0.5469 0.9706
eg:产生5阶两位数随机整数矩阵A,再产生均值为0.6,方差为0.1的5阶矩阵B,再产生一个5阶单位矩阵C。验证(A+B)✖C =C✖(A+B)
>> A = fix(10+(99-10+1)*rand(5))
A =
55 22 83 32 62
72 23 31 65 59
90 33 93 52 92
96 85 41 41 35
59 32 27 84 78
>> B = 0.6 + sqrt(0.1)*randn(5)
B =
0.8641 0.6332 0.5739 0.3192 0.7549
0.5229 0.8284 -0.0113 0.6317 0.8338
0.6682 1.4176 0.4612 0.4278 1.1413
0.2313 0.3891 0.0325 0.6960 0.5386
0.2370 0.6592 0.8658 0.4102 -0.0762
>> C = eye(5)
C =
1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 1
>> (A+B)*C == C*(A+B)
ans =
5×5 logical 数组
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
2、用于专门学科的特殊矩阵
【1】n阶魔方阵:由1,2,3,……,n^2 组成,并且矩阵的每一行,每一列,主、副对角线上元素之和相等。和为(n+n^3)/2
>> %产生8阶魔方阵求其每行,每列元素和
>> M = magic(8)
M =
64 2 3 61 60 6 7 57
9 55 54 12 13 51 50 16
17 47 46 20 21 43 42 24
40 26 27 37 36 30 31 33
32 34 35 29 28 38 39 25
41 23 22 44 45 19 18 48
49 15 14 52 53 11 10 56
8 58 59 5 4 62 63 1
>> sum(M(1,:))
ans =
260
>> sum(M(:,1))
ans =
260
【2】范德蒙矩阵
>> N = vander(1:5)
N =
1 1 1 1 1
16 8 4 2 1
81 27 9 3 1
256 64 16 4 1
625 125 25 5 1
【3】希尔伯特矩阵
>> format rat
>> M = hilb(4)
M =
1 1/2 1/3 1/4
1/2 1/3 1/4 1/5
1/3 1/4 1/5 1/6
1/4 1/5 1/6 1/7
【4】伴随矩阵

matlab生成伴随矩阵的函数:compan§,p为多项式系数向量。高次幂在前,低次幂在后。
生成x^3 -2*x^2 -5*x +6的伴随矩阵
>> p = [1,-2,-5,6];
>> A = compan(p)
A =
2 5 -6
1 0 0
0 1 0
【5】帕斯卡矩阵
根据二项式定理,(x+y)^n 展开后的系数随着n的增大组成的三角形表,这个三角形成为杨辉三角。
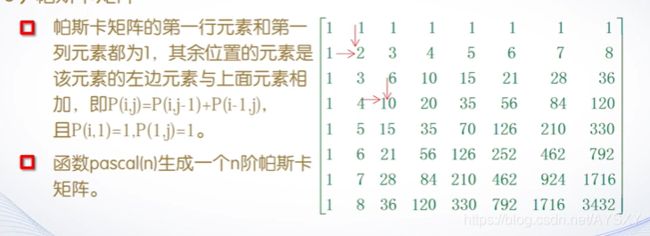
>> format rat
>> p = pascal(5)
p =
1 1 1 1 1
1 2 3 4 5
1 3 6 10 15
1 4 10 20 35
1 5 15 35 70
矩阵变换
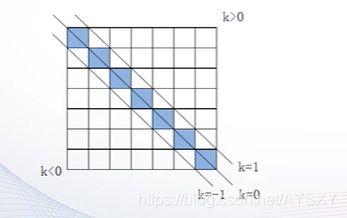
【1】提取矩阵的对角线元素
diag(A):提取矩阵A的主对角线元素,产生一个列向量。
diag(A,k):提取矩阵A的第k条对角线元素,产生一个列向量。
>> A
A =
1 1 0
1 0 5
1 10 2
>> diag(A)
ans =
1
0
2
>> diag(A,1)
ans =
1
5
>> diag(A,-1)
ans =
1
10
【2】构造对角阵
diag(X):以向量x为主对角线元素,产生对角矩阵
diag(X,k):以向量x的第K条对角线元素,产生对角矩阵
>> diag([1,2,3])
ans =
1 0 0
0 2 0
0 0 3
>> diag([1,2,3],1)
ans =
0 1 0 0
0 0 2 0
0 0 0 3
0 0 0 0
eg:A为5阶矩阵,将A的第一行元素乘以1,第一行元素乘以1,第二行元素乘以2,第三行元素乘以3,第四行元素乘以4,第5行元素乘以5。
>> A =[7,0,1,0,5;3,5,4,2,7;9,3,5,3,4;1,1,6,7,3;4,0,2,3,0]
A =
7 0 1 0 5
3 5 4 2 7
9 3 5 3 4
1 1 6 7 3
4 0 2 3 0
>> D = diag(1:5)
D =
1 0 0 0 0
0 2 0 0 0
0 0 3 0 0
0 0 0 4 0
0 0 0 0 5
>> D*A
ans =
7 0 1 0 5
6 10 8 4 14
27 9 15 9 12
4 4 24 28 12
20 0 10 15 0
【3】求一个矩阵的上三角阵和下三角阵
triu(A):提取矩阵A的主对角线以上元素。
triu(A,k):提取矩阵A的第k条对角线以上元素。
tril(A):提取矩阵A的主对角线以下元素。
tril(A,k):提取矩阵A的第k条对角线以下元素。
>> A
A =
7 0 1 0 5
3 5 4 2 7
9 3 5 3 4
1 1 6 7 3
4 0 2 3 0
>> triu(A)
ans =
7 0 1 0 5
0 5 4 2 7
0 0 5 3 4
0 0 0 7 3
0 0 0 0 0
>> triu(A,1)
ans =
0 0 1 0 5
0 0 4 2 7
0 0 0 3 4
0 0 0 0 3
0 0 0 0 0
>> tril(A)
ans =
7 0 0 0 0
3 5 0 0 0
9 3 5 0 0
1 1 6 7 0
4 0 2 3 0
>> tril(A,-1)
ans =
0 0 0 0 0
3 0 0 0 0
9 3 0 0 0
1 1 6 0 0
4 0 2 3 0
【4】矩阵的转置
转置运算符是小数点后面接单引号(. ‘)
共轭转置,其运算符是单引号(’),它在转置的基础上还要 取每个数的复共轭。
Note:如果矩阵元素为实数,则其转置和共轭转置是一样的。如果矩阵元素为复数,则其转置和共轭转置是不一样的。
>> A
A =
7 0 1 0 5
3 5 4 2 7
9 3 5 3 4
1 1 6 7 3
4 0 2 3 0
>> A.'
ans =
7 3 9 1 4
0 5 3 1 0
1 4 5 6 2
0 2 3 7 3
5 7 4 3 0
>> A'
ans =
7 3 9 1 4
0 5 3 1 0
1 4 5 6 2
0 2 3 7 3
5 7 4 3 0
>> B = [1,2;3+4i,1-2i]
B =
1.0000 + 0.0000i 2.0000 + 0.0000i
3.0000 + 4.0000i 1.0000 - 2.0000i
>> B.'
ans =
1.0000 + 0.0000i 3.0000 + 4.0000i
2.0000 + 0.0000i 1.0000 - 2.0000i
>> B'
ans =
1.0000 + 0.0000i 3.0000 - 4.0000i
2.0000 + 0.0000i 1.0000 + 2.0000i
【5】矩阵的旋转
rot90(A,k):将矩阵A逆时针方向旋转90度的k倍,k为1时可省略。
>> A
A =
7 0 1 0 5
3 5 4 2 7
9 3 5 3 4
1 1 6 7 3
4 0 2 3 0
>> rot90(A,2)
ans =
0 3 2 0 4
3 7 6 1 1
4 3 5 3 9
7 2 4 5 3
5 0 1 0 7
【6】矩阵的翻转
fliplr(A):将矩阵A进行左右翻转。
flipud(A):将矩阵A进行上下翻转。
>> A
A =
7 0 1 0 5
3 5 4 2 7
9 3 5 3 4
1 1 6 7 3
4 0 2 3 0
>> fliplr(A)
ans =
5 0 1 0 7
7 2 4 5 3
4 3 5 3 9
3 7 6 1 1
0 3 2 0 4
>> flipud(A)
ans =
4 0 2 3 0
1 1 6 7 3
9 3 5 3 4
3 5 4 2 7
7 0 1 0 5
eg:验证魔方阵的主对角线与副对角线元素和相等。
>> B = magic(5)
B =
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9
>> D1 = diag(B)
D1 =
17
5
13
21
9
>> sum(D1)
ans =
65
>> C = fliplr(B)
C =
15 8 1 24 17
16 14 7 5 23
22 20 13 6 4
3 21 19 12 10
9 2 25 18 11
>> D2 = diag(C)
D2 =
15
14
13
12
11
>> sum(D2)
ans =
65
【7】矩阵求逆
inv(A):求方阵A的逆矩阵。
>> B
B =
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9
>> inv(B)
ans =
-0.0049 0.0512 -0.0354 0.0012 0.0034
0.0431 -0.0373 -0.0046 0.0127 0.0015
-0.0303 0.0031 0.0031 0.0031 0.0364
0.0047 -0.0065 0.0108 0.0435 -0.0370
0.0028 0.0050 0.0415 -0.0450 0.0111
>> format rat
>> inv(B)
ans =
-77/15600 133/2600 -23/650 3/2600 53/15600
89/2063 -97/2600 -3/650 33/2600 23/15600
-59/1950 1/325 1/325 1/325 71/1950
73/15600 -17/2600 7/650 113/2600 -577/15600
43/15600 1/200 27/650 -9/200 98/8837
A=[1,2,3;1,4,9;1,8,7] b=[5,-2,6]^T
AX=b X =A的逆乘以b
>> b=[5,-2,6]
b =
5 -2 6
>> A = [1,2,3;1,4,9;1,8,27]
A =
1 2 3
1 4 9
1 8 27
>> b = b.'
b =
5
-2
6
>> X = inv(A)*b
X =
23
-29/2
11/3
矩阵求值
【1】求行列式
det(A):求方阵A所对应行列式的值
>> A = [1,1,0;1,0,5;1,10,2];
>> A
A =
1 1 0
1 0 5
1 10 2
>> det(A)
ans =
-47
【2】求矩阵的秩
秩:矩阵中线性无关的行数或列数
rank(A):求矩阵A的秩
>> B = [1,1,0;1,10,2;1,1,0]
B =
1 1 0
1 10 2
1 1 0
>> rank(B)
ans =
2
【3】求矩阵的迹
矩阵的迹等于矩阵的对角线之和,也等于矩阵特征值之和。
>> A
A =
1 1 0
1 0 5
1 10 2
>> trace(A)
ans =
3
【4】求向量和矩阵的范数
向量的3种常用范数
向量一范数:向量元素的绝对值和-norm(A,1)
向量二范数:向量元素的绝对值平方和的平方根-norm(A,2)
向量无穷大范数:所有向量元素绝对值的最大值-norm(A,inf)
矩阵的3种常用范数
矩阵一范数:矩阵列元素的绝对值和的最大值-norm(A,1)
矩阵二范数:矩阵的转置乘以矩阵的最大特征值的平方根-norm(A,2)
矩阵无穷大范数:所有矩阵行元素绝对值和的最大值-norm(A,inf)
>> B =[1,2,3];
>> norm(B,1)
ans =
6
>> norm(B,2)
ans =
3.7417
>> norm(B,inf)
ans =
3
>> A
A =
1 1 0
1 0 5
1 10 2
>> norm(A,1)
ans =
11
>> norm(A,2)
ans =
10.3757
>> norm(A,inf)
ans =
13
【5】求矩阵的条件数
矩阵A的条件数=A的范数与A的逆的范数的乘积
cond(A,1):计算A一范数下的条件数
cond(A,2):计算A二范数下的条件数
cond(A,1):计算A无穷范数下的条件数
eg:求2~10阶希尔伯特矩阵的条件数
>> for n=2:10
c(n) = cond(hilb(n))
end
>> c'
ans =
1.0e+13 *
0
0.000000000001928
0.000000000052406
0.000000001551374
0.000000047660725
0.000001495105864
0.000047536735691
0.001525757556663
0.049315340455101
1.602502816811318
矩阵的特征值与特征向量
设A是n阶方阵,如果存在常数λ和n维非零列向量x,使得等式Ax=λx成立,则称λ为A的特征值,x是对应特征值入的特征向量。
E=eig(A)∶求矩阵A的全部特征值,构成向量E。
[X,D]=eig(A):求矩阵A的全部特征值,构成对角阵D,并产生矩阵X,X各列是相应的特征向量。
>> A = [1,1,0;1,0,5;1,10,2];
>> [X,D] = eig(A)
X =
0.0722 0.9751 0.0886
0.5234 -0.0750 -0.6356
0.8490 -0.2089 0.7669
D =
8.2493 0 0
0 0.9231 0
0 0 -6.1723
稀疏矩阵
【1】矩阵的存储方式
1.完全存储方式
2.稀疏存储方式-只按列存储非零元素的值及其位置
【2】稀疏矩阵存储方式的产生
1.完全存储方式和稀疏存储方式之间的转换
A=sparse(S):将矩阵S转化为稀疏存储方式的矩阵A。
S=fullA):将矩阵A转化为完全存储方式的矩阵S。
>> A = sparse(eye(5))
A =
(1,1) 1
(2,2) 1
(3,3) 1
(4,4) 1
(5,5) 1
>> B = full(A)
B =
1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 1