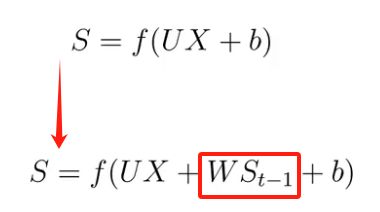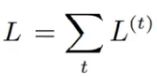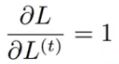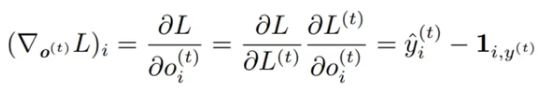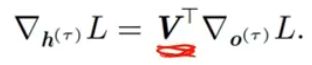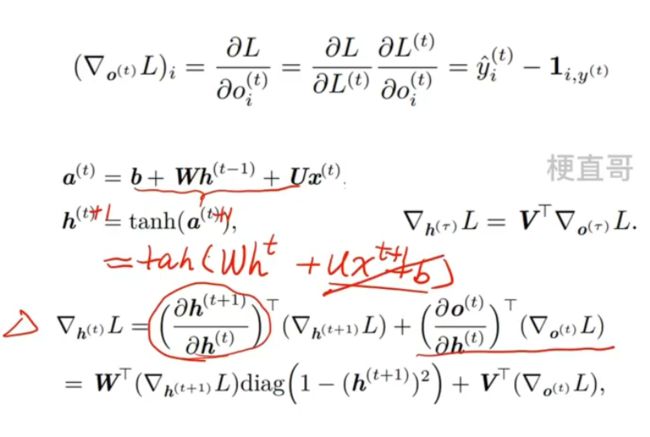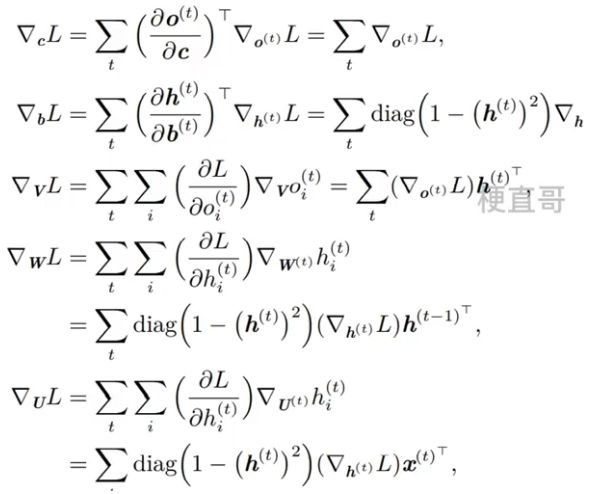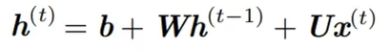深度学习 | 基本循环神经网络

---

1、序列建模

1.1、序列数据

        序列数据 —— 时间

        不同时间上收集到的数据，描述现象随时间变化的情况。

        序列数据 —— 文本

        由一串有序的文本组成的序列，需要进行分词。

                

        序列数据 —— 图像

        有序图像组成的序列，后一帧图像可能会受前一帧的影响

                

1.2、序列模型

        Sequence Model：用于处理和预测序列数据的模型

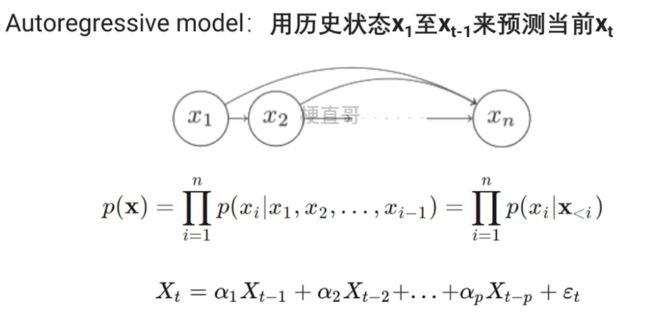
1.2.1、自回归模型 AR模型

        

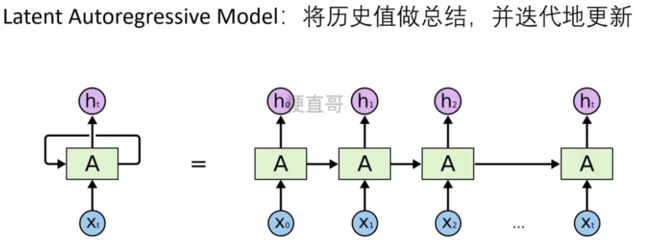
1.2.2、隐变量自回归模型        

        RNN属于隐变量自回归模型。

        防止 history 过长。

        动态变化的隐变量链也称为隐变量动态模型。

        

---

---

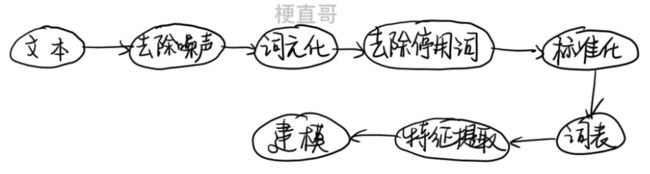
2、文本数据预处理

主要流程

        中文文本需要用分词算法来完成分词；

        英文文本需要拼写检查、词干提取词形还原。

        分词 也叫 词元化。

        

②、去除噪声 Text Cleaning

        删除文本中不相关或者无用的信息，提高文本处理的效率，

        非文本内容可直接使用re表达式进行删除。

        停用词：英文介词、代词、连词等，中文助词、量词、叹词等。

        

③、词元化 / 分词 / 令牌化 Tokenization

        把输入的文本流，切分成一个个子串。

④、去除停用词

        文本中出现频率过高或者并不具有实际意义的词。

⑤、标准化 主要针对英文

        词干提取 (stemming)：抽取词的词干或词根形式

        词形还原(lemmatization) ：把任何形式语言词汇还原为一般形式

⑥、构造词表

        将文本中出现的所有词汇组成列表

        1、遍历数据集，统计词频

        2、过滤高频词和低频词，保留中间频率词

        3、为每个词分配一个编号，并建立词表

 ⑦、特征提取 

*** 存疑

        词袋模型 ，不考虑每个单词的顺序，只是统计每个词出现的次数。

                Bag of Words：根据词表中单词在句子中出现次数转化为向量。

                —— 然后对这样的一个 矩阵/数组/列表 进行编码就可以对他进行向量化了。

                

        N-gram模型：基于概率的判别式语言模型，可以捕捉到词与词之间的关系。

                将文本表示成连续的n个词的序列。

                

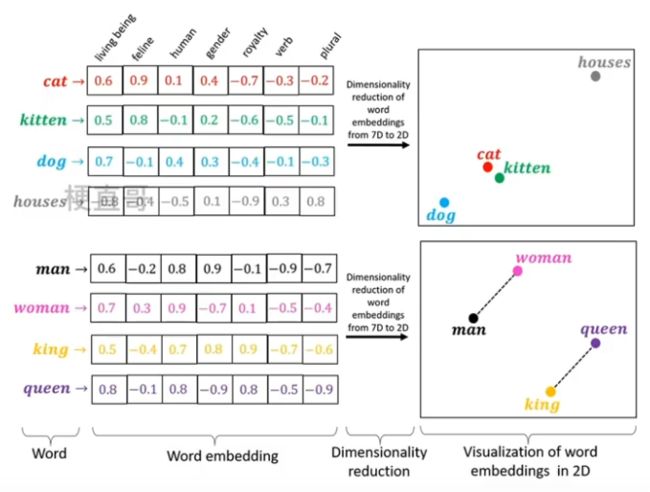
        词嵌入 Word Embedding：是将词表现为实数向量的一种方法，可以捕捉到词和词之间的语义和语法关系，使得词之间可以通过数学计算进行比较和计算。

        常用的词嵌入模型包括：

                word2vec：通过预测上下文中的词来学习词向量。

                GloVe：通过统建词和词之间的贡献的关系。

                

---

---

3、循环神经网络 Recurrent Neura Network

        为什么全连接网络处理不好序列的数据？

        因为全连接网络结构上就没有顺序相关的这种处理模块。

---

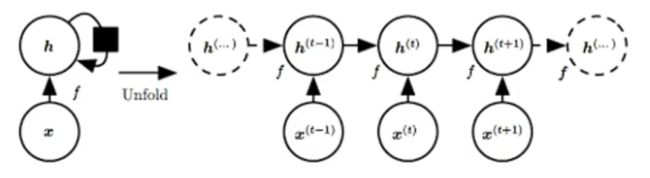
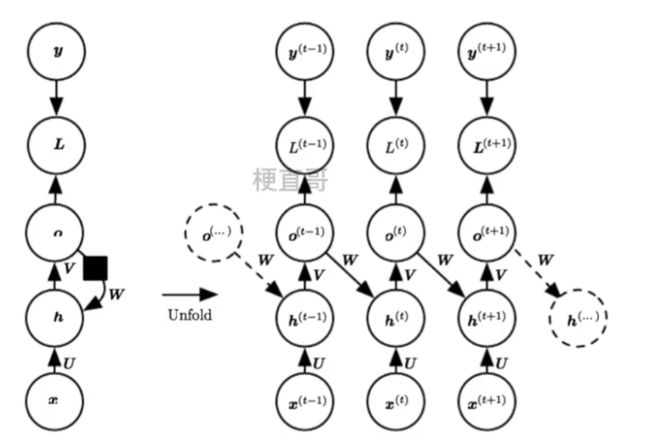
3.1、展开计算图

         计算图是形式化一组计算结构的形式。

         展开 (unfolding)计算图导致深度网络结构中的参数共享。

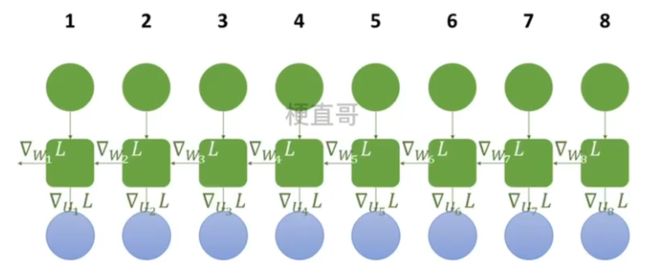
         箭头表示信息流动，小黑方块表示一种计算关系。

        

---

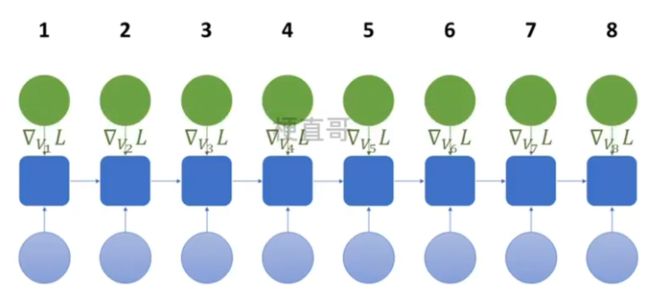
3.2、网络结构及变体

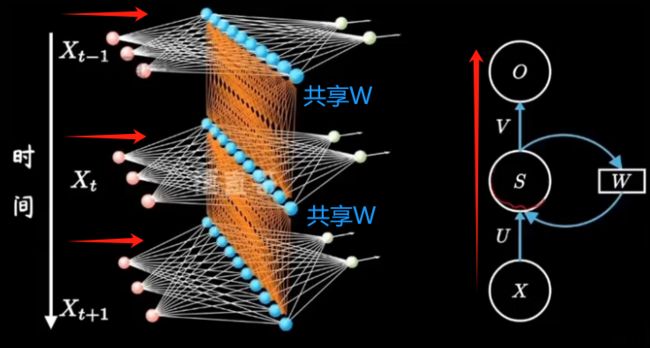
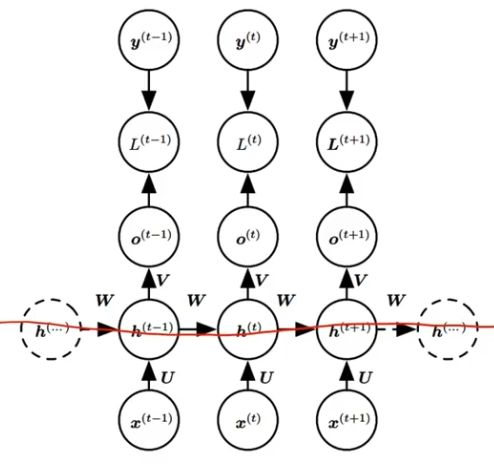
网络结构

        在隐藏层之间构建了循环层。

        

        红色小球代表输入数据。每一行的网络都可以看成一个完整的全连接层。

        U 是当前时间步的输入到隐藏层的一个权重；

        W 是上一个时间步的隐藏状态再到当前隐藏状态的一个权重；

        V 是隐藏层到输出层的权重。

        

        正是因为有了隐藏层之间黄色的连线，隐藏层间连接形成循环神经网络，模型由此具备了记忆能力。

        不是网络结构更加复杂了，只是把不同时间隐藏层的状态记住了，换句话说就是不同的隐藏层之间共享W。

        

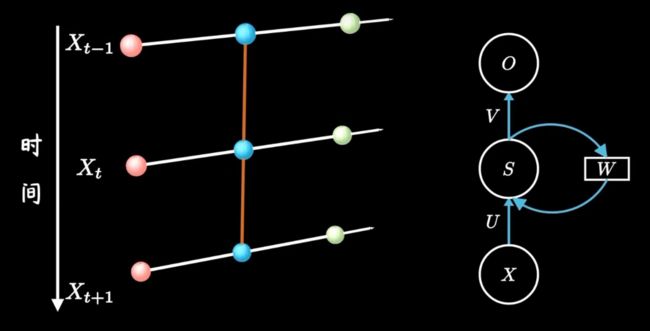
        若从隐藏层的变换函数来说，就是多了一个方向的输入。

        

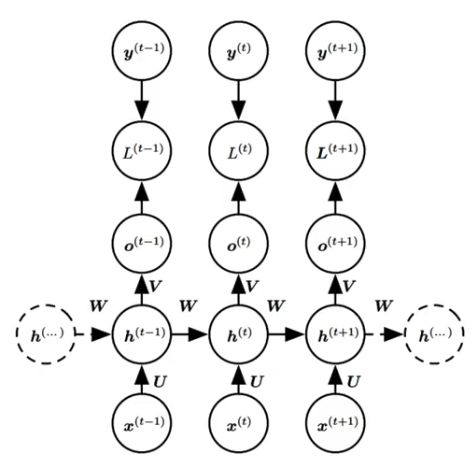
        换个表示方式：

                h 是隐藏层的状态，L 是输出的损失，y 是训练目标，通过计算 y 和 o 之间的误差 L 来训练整个网络。

                U：输入和隐藏层之间的变换；

                V：隐藏层和输出 o 之间的变换；

                W：隐藏层之间共享的参数，可以叫 state transition 或者 dynamics。

                三组权重参数 U V W 一起训练。

        

---

网络结构变体

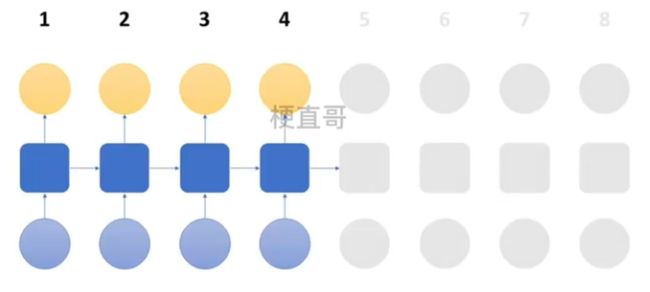
3.2.1、free-running mode

        训练迭代过程早期的RNN预测能力非常弱，几乎不能给出好的生成结果。如果某一个unit产生了垃圾结果，必然会影响后面一片unit的学习。 

        因为没有从 h t-1向前传播的直接链接，信息是通过 h t-1 产生的预测间接的链接到当前的隐藏层变量 ht，

        这使得RNN网络结构简化，相对来说更容易训练，这是因为每个时间步可以与其他时间步进行分离训练，允许训练期间有更多的并行化。

        

其实RNN存在着两种训练模式(mode)：

        free-running mode
         teacher-forcing mode

        free-running mode就是大家常见的那种训练网络的方式：上一个state的输出作为下一个state的输入。

        而Teacher Forcing是一种快速有效地训练循环神经网络模型的方法，该模型使用来自先验时间步长的输出作为输入。

---

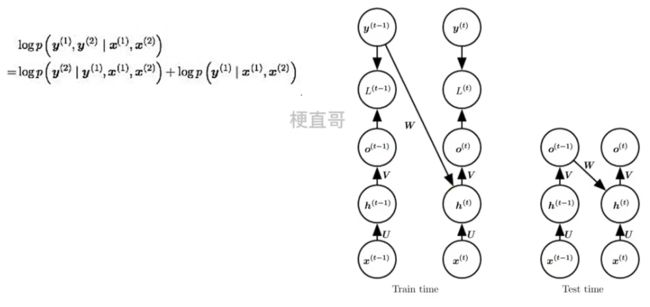
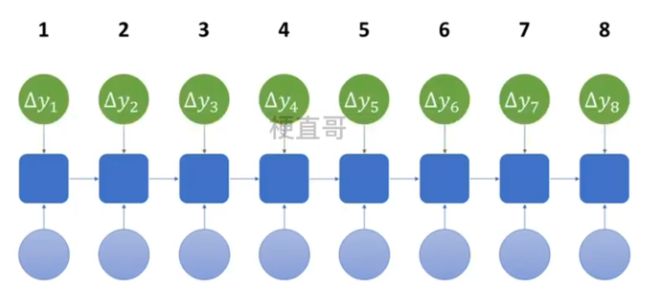
3.2.2、Teacher Forcing

        Teacher Forcing是一种快速有效地训练循环神经网络模型的方法，该模型使用来自先验时间步长的输出作为输入。

        它是一种网络训练方法，对于开发用于机器翻译，文本摘要，图像字幕的深度学习语言模型以及许多其他应用程序至关重要。它每次不使用上一个state的输出作为下一个state的输入，而是直接使用训练数据的标准答案(ground truth)的对应上一项作为下一个state的输入。

        因为依赖标签数据，相当于解耦了，在训练过程中，模型会有较好的效果，但是在测试的时候因为不能得到ground truth的支持，所以如果目前生成的序列在训练过程中有很大不同，模型就会变得脆弱。

        也就是说，这种模型的cross-domain能力会更差，也就是如果测试数据集与训练数据集来自不同的领域，模型的performance就会变差。

         

---

---

*** 存疑

4、RNN的反向传播 —— BPTT 随时间反向传播算法

        RNN的反向传播称为 BPTT算法。回到过去改变权重。

        Backpropagation Through Time：将序列数据的每个时间步看作一层，然后在每个时间步上使用标准 BP 算法来计算梯度。

        

        对于每一个时间步 t  ，计算损失函数对网络参数的梯度 L(t)，

        并将这些梯度的值累加起来得到总的损失：

        然后通过计算总损失的偏导数来更新网络参数。

        对于每一个节点 N ，我们需要 N 自己的 和 N 后面的所有的节点的梯度递归的计算 N 的 梯度：

        因为 L = L1+L2+L3+...+Lt，所以

        因为，他们之间的差我们通常会用交叉熵损失衡量，

                采用负对数似然做损失，其中

        则，其中 1 是真值矩阵。

        从序列的末尾开始，反向递归计算各个部分各个节点以及他们参数的偏导，这就是BPTT的目标了。

        首先我们来看它的末尾。

        最后一步 假如是 时间 τ，所以只需要对 o (τ) 求偏导数就可以了。

        根据输出方程，得出

        再来看 ht：

                

        

                 

        

整体流程：

        1、训练数据前向传播

                

        2、计算各时间预测值 y hat 与训练值比较，计算总损失 L

                

                

        3、反向传播求各个参数的梯度

                

                

        4、根据梯度更新参数

                

---

---

5、循环神经网络代码实现

5.1、时间序列数据预测

1、数据集引入

pandas_datareader 库用于从网络获取经济数据，其中 get_data_fred 函数用于从 FRED (Federal Reserve Economic Data) 获取数据。在这个例子里，GS10 是美国国债收益率的代码，它将会返回与美国10年期国债收益率相关的数据。 

import pandas_datareader as pdr
gs10 = pdr.get_data_fred('GS10')
gs10.head()

	GS10
DATE
2018-02-01	2.86
2018-03-01	2.84
2018-04-01	2.87
2018-05-01	2.98
2018-06-01	2.91

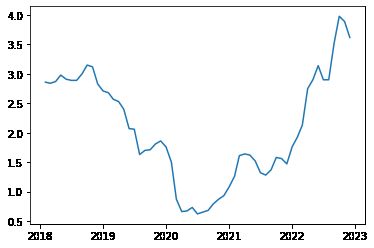
绘制数据图像

import matplotlib.pyplot as plt
plt.plot(gs10)
plt.show()

序列数据没办法直接使用，需要进行预处理。

        对原始数据进行切分。

        n 是超参数。用多少个去预测下一个元素。

        

2、数据预处理

初始化特征序列，列数就是预测序列的长度 seq，行数是 n - seq。

行数不是 n 的原因是因为最初的几条信息无法用来构建数据集，他们缺失了更早的时序信息。

• X_feature 是一个形状为 (num-seq_len, seq_len) 的全零张量，用于存储特征矩阵。
• 在循环中，从 x 中切片取出长度为 num-seq_len 的子序列，并将它们赋值给 X_feature 的不同列，以构建特征矩阵。

而这段代码的最后一行 y_label = x[seq_len:].reshape((-1, 1)) 的作用是构建输出标签 y_label，具体来说：

• x[seq_len:] 表示从 x 中切片取出从索引 seq_len 开始到末尾的子序列，即去掉了前 seq_len 个时间步的数据。
• .reshape((-1, 1)) 将切片得到的一维数组重新调整为形状为 (-1, 1) 的二维数组。其中 -1 表示自动计算该维度的大小，这里表示将数组变成一列。

特征矩阵 X_feature 的前 num-seq_len 个样本和输出标签 y_label 的前 num-seq_len 个样本作为输入。 

import torch
from torch.utils.data import DataLoader, TensorDataset

num = len(gs10)                           # 总数据量
x = torch.tensor(gs10['GS10'].to_list())  # 股价列表
seq_len = 6                               # 预测序列长度
batch_size = 4                            # 设置批大小

X_feature = torch.zeros((num - seq_len, seq_len))      # 全零初始化特征矩阵，num-seq_len行，seq_len列
for i in range(seq_len):
    X_feature[:, i] = x[i: num - seq_len + i]    # 为特征矩阵赋值
y_label = x[seq_len:].reshape((-1, 1))           # 真实结果列表

train_loader = DataLoader(TensorDataset(X_feature[:num-seq_len], 
    y_label[:num-seq_len]), batch_size=batch_size, shuffle=True)  # 构建数据加载器

train_loader.dataset[:batch_size]

(tensor([[2.8600, 2.8400, 2.8700, 2.9800, 2.9100, 2.8900],
         [2.8400, 2.8700, 2.9800, 2.9100, 2.8900, 2.8900],
         [2.8700, 2.9800, 2.9100, 2.8900, 2.8900, 3.0000],
         [2.9800, 2.9100, 2.8900, 2.8900, 3.0000, 3.1500]]),
 tensor([[2.8900],
         [3.0000],
         [3.1500],
         [3.1200]]))

---

先用  基本神经网络模型 看看效果：

3、构建基本神经网络模型

from torch import nn
from tqdm import *

class Model(nn.Module):
    def __init__(self, input_size, output_size, num_hiddens):
        super().__init__()
        self.linear1 = nn.Linear(input_size, num_hiddens)
        self.linear2 = nn.Linear(num_hiddens, output_size)

    
    def forward(self, X):
        output = torch.relu(self.linear1(X))
        output = self.linear2(output)
        return output

# 定义超参数
input_size = seq_len
output_size = 1
num_hiddens = 10  
lr = 0.01

# 建立模型
model = Model(input_size, output_size, num_hiddens)
criterion = nn.MSELoss(reduction='none')
trainer = torch.optim.Adam(model.parameters(), lr)

4、模型训练

num_epochs = 20
loss_history = []

for epoch in tqdm(range(num_epochs)):
    # 批量训练
    for X, y in train_loader:
        trainer.zero_grad()
        y_pred = model(X)
        loss = criterion(y_pred, y)
        loss.sum().backward()
        trainer.step()
     # 输出损失
    model.eval()
    with torch.no_grad():
        total_loss = 0
        for X, y in train_loader:
            y_pred = model(X)
            loss = criterion(y_pred, y)
            total_loss += loss.sum()/loss.numel()
        avg_loss = total_loss / len(train_loader)
        print(f'Epoch {epoch+1}: Validation loss = {avg_loss:.4f}')
        loss_history.append(avg_loss)
    
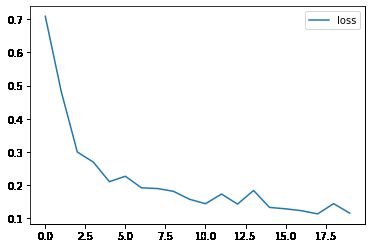
# 绘制损失和准确率的曲线图
import matplotlib.pyplot as plt
plt.plot(loss_history, label='loss')
plt.legend()
plt.show()

100%|██████████| 20/20 [00:00<00:00, 130.13it/s]
Epoch 1: Validation loss = 0.7089
Epoch 2: Validation loss = 0.4812
Epoch 3: Validation loss = 0.2999
Epoch 4: Validation loss = 0.2695
Epoch 5: Validation loss = 0.2106
Epoch 6: Validation loss = 0.2270
Epoch 7: Validation loss = 0.1922
Epoch 8: Validation loss = 0.1899
Epoch 9: Validation loss = 0.1816
Epoch 10: Validation loss = 0.1578
Epoch 11: Validation loss = 0.1442
Epoch 12: Validation loss = 0.1734
Epoch 13: Validation loss = 0.1430
Epoch 14: Validation loss = 0.1842
Epoch 15: Validation loss = 0.1331
Epoch 16: Validation loss = 0.1289
Epoch 17: Validation loss = 0.1232
Epoch 18: Validation loss = 0.1135
Epoch 19: Validation loss = 0.1444
Epoch 20: Validation loss = 0.1159

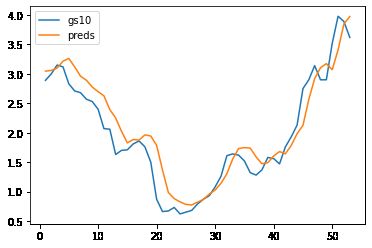
 5、模型预测

单步预测：使用序列模型对序列数据进行预测，只预测序列的下一个元素。

preds = model(X_feature)
time = torch.arange(1, num+1, dtype= torch.float32)  # 时间轴

plt.plot(time[:num-seq_len], gs10['GS10'].to_list()[seq_len:num], label='gs10')
plt.plot(time[:num-seq_len], preds.detach().numpy(), label='preds')
plt.legend()
plt.show()

---

5.2、RNN模型预测

1、数据预处理

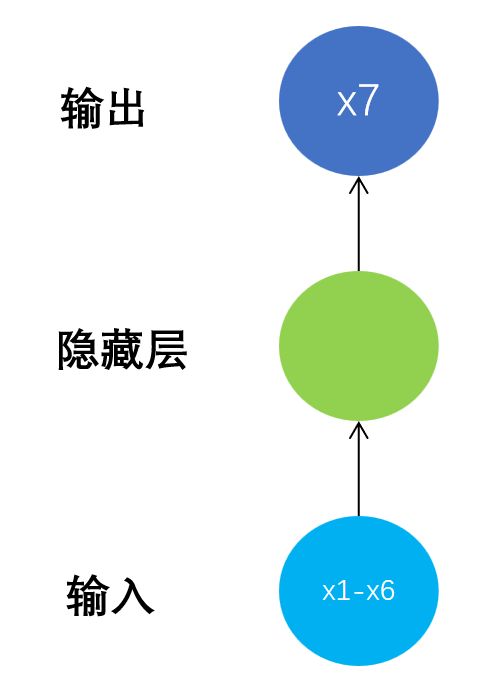
        一般神经网络模型结构如下： N to 1

        

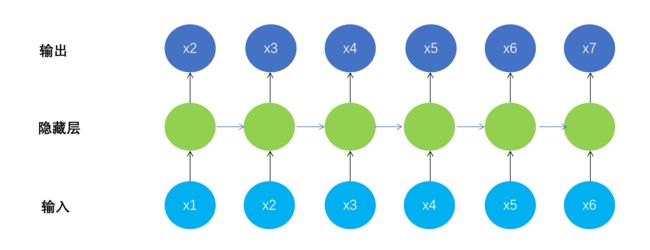
        循环神经网络模型结构如下：N to N

        

       此时模型输出不再是一个简单的标量，而是x2到x7这样一个向量。

        Y_label变成了一个矩阵。

        为了使用RNN进行计算，需要对  X_feature 进行升维操作。

 

• x[i:num-seq_len+i] 表示从 x 中提取从索引 i 开始，长度为 seq_len 的子序列。

• 这个操作用于构建输入特征 X_feature。在每次循环中，我们将从 x 中切出长度为 seq_len 的子序列，并将它们放到 X_feature 的不同列中，以构建模型的输入。

• x[i+1:num-seq_len+i+1] 表示从 x 中提取从索引 i+1 开始，长度为 seq_len 的子序列。

• 这个操作用于构建输出标签 Y_label。在每次循环中，我们将从 x 中切出长度为 seq_len 的另一个子序列，并将它们放到 Y_label 的不同列中，以构建模型的输出。

综上所述，这些切片操作帮助我们按照滑动窗口的方式从时间序列数据中提取输入特征和对应的输出标签，以便用于训练模型。

import torch
from torch.utils.data import DataLoader, TensorDataset

num = len(gs10)                           # 总数据量，59
x = torch.tensor(gs10['GS10'].to_list())  # 股价列表
seq_len = 6                               # 预测序列长度
batch_size = 4                            # 设置批大小

X_feature = torch.zeros((num - seq_len, seq_len))      # 构建特征矩阵，num-seq_len行，seq_len列，初始值均为0
Y_label = torch.zeros((num - seq_len, seq_len))        # 构建标签矩阵，形状同特征矩阵
for i in range(seq_len):
    X_feature[:, i] = x[i: num - seq_len + i]    # 为特征矩阵赋值
    Y_label[:, i] = x[i+1: num - seq_len + i + 1]    # 为标签矩阵赋值

train_loader = DataLoader(TensorDataset(
    X_feature[:num-seq_len].unsqueeze(2), Y_label[:num-seq_len]),
    batch_size=batch_size, shuffle=True)  # 构建数据加载器

在代码中，最后一个 unsqueeze(2) 的目的是为了将 X_feature 的维度从 (num-seq_len, seq_len) 转换为 (num-seq_len, seq_len, 1)。

在这段代码中，我们将时间序列数据作为特征矩阵 X_feature，其形状为 (num-seq_len, seq_len)。然而，RNN 模型通常要求输入为三维张量，其中最后一个维度表示特征的数量。

通过使用 unsqueeze(2) 函数，我们在 X_feature 张量上插入一个维度，将其形状从 (num-seq_len, seq_len) 扩展为 (num-seq_len, seq_len, 1)。这样做是为了与 RNN 模型的输入要求相匹配，其中最后一个维度表示特征的数量（这里是 1）。

需要注意的是，对于 RNN 模型来说，时间序列数据通常被看作是一个三维张量，在第一个维度上表示样本的索引，在第二个维度上表示时间步的索引，在第三个维度上表示特征值的索引。因此，为了适应 RNN 模型的输入要求，我们需要将时间序列数据转换成三维张量的形式，即 (num-seq_len, seq_len, 1)。

总之，最后的 unsqueeze(2) 操作是为了将时间序列数据转换为 RNN 模型所需的三维张量形式，以便进行训练和预测。

train_loader.dataset[:batch_size]

(tensor([[[2.8600],
          [2.8400],
          [2.8700],
          [2.9800],
          [2.9100],
          [2.8900]],
 
         [[2.8400],
          [2.8700],
          [2.9800],
          [2.9100],
          [2.8900],
          [2.8900]],
 
         [[2.8700],
          [2.9800],
          [2.9100],
          [2.8900],
          [2.8900],
          [3.0000]],
 
         [[2.9800],
          [2.9100],
          [2.8900],
          [2.8900],
          [3.0000],
          [3.1500]]]),
 tensor([[2.8400, 2.8700, 2.9800, 2.9100, 2.8900, 2.8900],
         [2.8700, 2.9800, 2.9100, 2.8900, 2.8900, 3.0000],
         [2.9800, 2.9100, 2.8900, 2.8900, 3.0000, 3.1500],
         [2.9100, 2.8900, 2.8900, 3.0000, 3.1500, 3.1200]]))

2、构建循环神经网络模型

因为每个元素是一个一个元素输入再一个一个输出，所以input_size和output_size都设置为1。

在 PyTorch 中，张量的 size() 方法可以返回张量的形状，也就是它在每个维度上的长度。对于一个二维张量（即矩阵）来说，size() 方法返回一个元组 (num_rows, num_cols)，其中 num_rows 表示矩阵的行数，num_cols 表示矩阵的列数。

在深度学习中，通常使用小批量训练来提高模型的泛化能力和收敛速度，因此我们需要知道每个批次的样本数量。而批次大小实际上就是输入张量的第一个维度的长度，也就是 X.size(0) 的值。

因此，通过调用 X.size(0) 方法，我们可以获取输入张量 X 的批次大小，从而在 RNN 模型中进行相应的初始化和计算。

在 begin_state 方法中，将隐藏状态初始化为全零张量。在这个方法中，batch_size 参数默认值为 1，这是因为在某些情况下，我们可能只需要对单个样本进行前向传播，而不是一个批次的样本。

在深度学习中，通常会使用小批量训练来提高模型的泛化能力和收敛速度。但是，有时候也会需要对单个样本进行推断或生成，例如在生成文本时，我们可能逐步生成每个单词，而不是一次生成整个句子。此时，我们只需要一个样本的隐藏状态。

因此，在 begin_state 方法中，默认将 batch_size 设置为 1，以支持单个样本的处理。当我们需要处理多个样本时，可以通过将 batch_size 参数设置为相应的值来初始化相应大小的隐藏状态。

 

from torch import nn
from tqdm import *

class RNNModel(nn.Module):
    def __init__(self, input_size, output_size, num_hiddens, n_layers):
        super(RNNModel, self).__init__()
        self.num_hiddens = num_hiddens
        self.n_layers = n_layers
        self.rnn = nn.RNN(input_size, num_hiddens, n_layers, batch_first = True)
        self.linear = nn.Linear(num_hiddens, output_size)
       
    def forward(self, X):
        batch_size = X.size(0)
        state = self.begin_state(batch_size)
        output, state = self.rnn(X, state)
        output = self.linear(torch.relu(output))
        return output, state

    def begin_state(self, batch_size=1):
        return  torch.zeros(self.n_layers, batch_size, self.num_hiddens)

# 定义超参数
input_size = 1
output_size = 1
num_hiddens = 10
n_layers = 1
lr = 0.01

# 建立模型
model = RNNModel(input_size, output_size, num_hiddens, n_layers)
criterion = nn.MSELoss(reduction='none')
trainer = torch.optim.Adam(model.parameters(), lr)

3、训练

• y_pred: 维度为 (batch_size, seq_len, output_size)
• Y: 维度为 (batch_size, seq_len)

在损失函数计算部分，通过调用 squeeze() 方法对 y_pred 和 Y 进行了维度压缩，使得它们的维度变为 (batch_size, seq_len)。这样可以逐元素地计算损失函数。

num_epochs = 20
rnn_loss_history = []

for epoch in tqdm(range(num_epochs)):
    # 批量训练
    for X, Y in train_loader:
        trainer.zero_grad()
        y_pred, state = model(X)
        loss = criterion(y_pred.squeeze(), Y.squeeze())
        loss.sum().backward()
        trainer.step()
     # 输出损失
    model.eval()
    with torch.no_grad():
        total_loss = 0
        for X, Y in train_loader:
            y_pred, state = model(X)
            loss = criterion(y_pred.squeeze(), Y.squeeze())
            total_loss += loss.sum()/loss.numel()
        avg_loss = total_loss / len(train_loader)
        print(f'Epoch {epoch+1}: Validation loss = {avg_loss:.4f}')
        rnn_loss_history.append(avg_loss)
    
# 绘制损失曲线图
import matplotlib.pyplot as plt
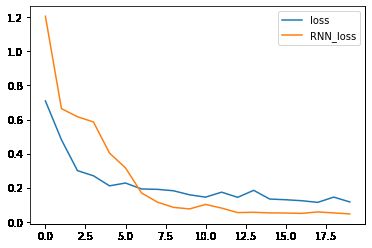
plt.plot(loss_history, label='loss')
plt.plot(rnn_loss_history, label='RNN_loss')
plt.legend()
plt.show()

 35%|███▌      | 7/20 [00:00<00:00, 62.68it/s]Epoch 1: Validation loss = 1.2063
Epoch 2: Validation loss = 0.6640
Epoch 3: Validation loss = 0.6163
Epoch 4: Validation loss = 0.5854
Epoch 5: Validation loss = 0.4029
Epoch 6: Validation loss = 0.3159
Epoch 7: Validation loss = 0.1687
Epoch 8: Validation loss = 0.1145
Epoch 9: Validation loss = 0.0840
Epoch 10: Validation loss = 0.0751
Epoch 11: Validation loss = 0.1014
Epoch 12: Validation loss = 0.0798
Epoch 13: Validation loss = 0.0535
100%|██████████| 20/20 [00:00<00:00, 63.90it/s]Epoch 14: Validation loss = 0.0552
Epoch 15: Validation loss = 0.0517
Epoch 16: Validation loss = 0.0510
Epoch 17: Validation loss = 0.0488
Epoch 18: Validation loss = 0.0574
Epoch 19: Validation loss = 0.0516
Epoch 20: Validation loss = 0.0457

4、预测

rnn_preds,_ = model(X_feature.unsqueeze(2))
preds.squeeze()
time = torch.arange(1, num+1, dtype= torch.float32)  # 时间轴

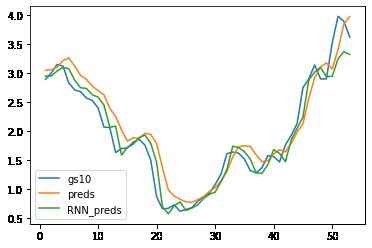
plt.plot(time[:num-seq_len], gs10['GS10'].to_list()[seq_len:num], label='gs10')
plt.plot(time[:num-seq_len], preds.detach().numpy(), label='preds')
plt.plot(time[:num-seq_len], rnn_preds[:,seq_len-1].detach().numpy(), label='RNN_preds')
plt.legend()
plt.show()

x

tensor([2.8600, 2.8400, 2.8700, 2.9800, 2.9100, 2.8900, 2.8900, 3.0000, 3.1500,
        3.1200, 2.8300, 2.7100, 2.6800, 2.5700, 2.5300, 2.4000, 2.0700, 2.0600,
        1.6300, 1.7000, 1.7100, 1.8100, 1.8600, 1.7600, 1.5000, 0.8700, 0.6600,
        0.6700, 0.7300, 0.6200, 0.6500, 0.6800, 0.7900, 0.8700, 0.9300, 1.0800,
        1.2600, 1.6100, 1.6400, 1.6200, 1.5200, 1.3200, 1.2800, 1.3700, 1.5800,
        1.5600, 1.4700, 1.7600, 1.9300, 2.1300, 2.7500, 2.9000, 3.1400, 2.9000,
        2.9000, 3.5200, 3.9800, 3.8900, 3.6200])

---

---

 6、RNN的长期依赖问题

什么是长期依赖？

        当前系统的状态，可能依赖很长时间之前系统状态。

        

长期记忆失效的原因 —— 权重矩阵连乘

        假定循环链接非常简单，去掉激活函数。

        

        h0 的系数乘指数级增长，W^t ，若W特征值的幅值如果小于1，那么就是指数级的衰减。

        则会导致类似于蝴蝶效应的现象，初始条件的很小变化就会导致结果严重的变化。

        

激活函数的选择

        RNN中可以用ReLU函数，但不能解决梯度消失、爆炸问题。

        对矩阵W的初始值敏感，十分容易引发数值问题。

        梯度的消失和爆炸沿着时间轴的级联导致的。

为什么CNN不会出现这个问题？

        因为CNN中每一层卷积的权重是不相同的，并且初始化时是独立的同分布的，因此可以互相抵消，多层之后一般不会引发数值问题。

        而RNN是共用相同的权重矩阵W，只有当W取在单位矩阵附近的时候才会有好的效果。

*** 存疑

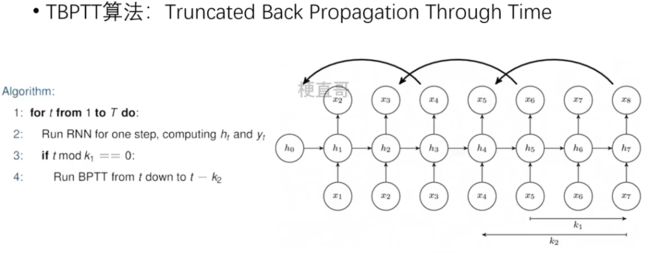
截断时间步 TBPTT算法

        每向前传播k1步，也向后传播k2步。

        

       

---

---

部分内容参考

【循环神经网络】5分钟搞懂RNN，3D动画深入浅出_哔哩哔哩_bilibili

一文弄懂关于循环神经网络(RNN)的Teacher Forcing训练机制_free-running mode-CSDN博客