代码随想录day18 二叉树开始各种方法尝试

513.找树左下角的值

题目

给定一个二叉树，在树的最后一行找到最左边的值。

示例 1:

思考

本题用层序遍历就很好解，最后一层的第一个数，就是最后一行最左边的值，这里需要用一个二维vector把每一层的数都存下来

代码

class Solution {

public:

    int findBottomLeftValue(TreeNode* root) {

        queue que;

        vector> res;

        que.push(root);

        while(!que.empty()) {

            int size = que.size();

            vector tmp;//把每一层都存起来，最后一层的第一个元素就是最底层最左边元素

            while(size--) {

                TreeNode* node = que.front();

                que.pop();

                tmp.push_back(node->val);

                if(node->left) que.push(node->left);

                if(node->right) que.push(node->right);

            }

            res.push_back(tmp);

        }

        return res[res.size()-1][0];

    }

};

112. 路径总和

题目

给定一个二叉树和一个目标和，判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和。

说明: 叶子节点是指没有子节点的节点。

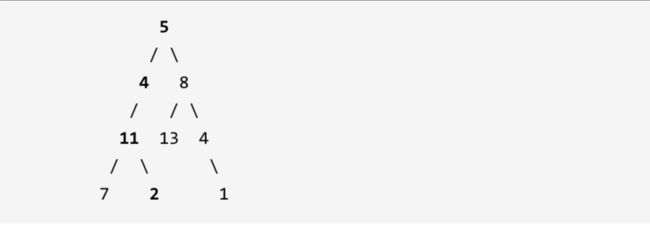
示例: 给定如下二叉树，以及目标和 sum = 22，

返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2。

思考

这题一看就是要用前序来做，但有个需要注意的点是需要用一个pair把结点和头结点到这个结点的和都存好，这样做的目的是在回溯中记录下每个结点的和，不然如果用int sum 的话在回溯过程中会出错，然后中左右的中是要判断该结点已经到底了并且和是否是targetSum。

代码

//  前序遍历

class Solution {

public:

    bool hasPathSum(TreeNode* root, int targetSum) {

        stack> stk;

        if(root == nullptr) return false;

        stk.push(pair(root,root->val));

        while(!stk.empty()) {

            pair node = stk.top();

            stk.pop();//这里是一个循环，压入一个回溯一个，要判断目前遍历的结点是否为叶子结点

            if(!node.first->left && !node.first->right && targetSum == node.second) return true;

            if(node.first->right) {

                stk.push(pair(node.first->right, node.second + node.first->right->val));

            }

            if(node.first->left) {

                stk.push(pair(node.first->left, node.second + node.first->left->val));

            }

        }

        return false;

    }

};

106.从中序与后序遍历序列构造二叉树

题目

根据一棵树的中序遍历与后序遍历构造二叉树。

注意: 你可以假设树中没有重复的元素。

例如，给出

• 中序遍历 inorder = [9,3,15,20,7]
• 后序遍历 postorder = [9,15,7,20,3] 返回如下的二叉树：

思考

初看有点蒙，感觉无从下手，看完卡哥视频才发现需要找到根结点，那么得从后序数组里找，最后一个数就是根结点，因为从左右中的顺序来说，中在最后，然后再中序数组中找到根结点，把其分为左右两个数组，同时根据中序数组的左右数组来确定后序数组的左右数组，因为左右数组的size都是相等的，这个技巧很关键，接着递归node->left、node->right就好，主要这里node->left、node->right是要等于递归的结果，而不是用if判断

代码

class Solution {

public:

    TreeNode* traversal(vector& inorder, vector& postorder) {

        if (postorder.size() == 0) return nullptr;// 第一步：如果数组大小为零的话，说明是空节点了。

        int root = postorder[postorder.size() - 1];// 第二步：如果不为空，那么取后序数组最后一个元素作为节点元素。

        TreeNode* node = new TreeNode(root);//新的treenode是这样创建

        int mid = 0;

        for(; mid < inorder.size(); mid++) {

            if(inorder[mid] == root) break;// 第三步：找到后序数组最后一个元素在中序数组的位置，作为切割点

        }

        vector leftInoroder(inorder.begin(), inorder.begin() + mid);

        vector rightInorder(inorder.begin() + mid + 1, inorder.end());// 第四步：切割中序数组，切成中序左数组和中序右数组 （顺序别搞反了，一定是先切中序数组，并且注意，这里要跳过mid，所以right数组是从mid+1开始）

        postorder.pop_back();

        vector leftPostorder(postorder.begin(), postorder.begin() + leftInoroder.size());

        vector rightPostorder(postorder.begin() + leftInoroder.size(), postorder.end());// 第五步：切割后序数组，切成后序左数组和后序右数组

        node->left = traversal(leftInoroder,leftPostorder);

        node->right = traversal(rightInorder, rightPostorder);// 第六步：递归处理左区间和右区间

        return node;

    }

    TreeNode* buildTree(vector& inorder, vector& postorder) {

        if(inorder.size() == 0 || postorder.size() == 0) return nullptr;

        return traversal(inorder, postorder);

    }

};