leetcode:105. 从前序与中序遍历序列构造二叉树
题目描述:
输入某二叉树的前序遍历和中序遍历的结果,请构建该二叉树并返回其根节点。
假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
示例 1:

Input: preorder = [3,9,20,15,7],
inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]
示例 2:
Input: preorder = [-1], inorder = [-1]
Output: [-1]
限制:
0 <= 节点个数 <= 5000
方法一:运用递归构造二叉树解题思路:
1.由前序遍历的结果知道,树的根节点为第一个元素,也是中序遍历中左子树与右子树的分界点。所以首先取出前序遍历的首节点,并作为构造二叉树的根节点。
2.在中序遍历中找到前序遍历首节点(即当前树的根节点)的位置,将中序遍历位于该节点左侧的节点划为左子树,位于该节点右侧的节点划为右子树,进行递归构造二叉树左子树与右子树的构造。
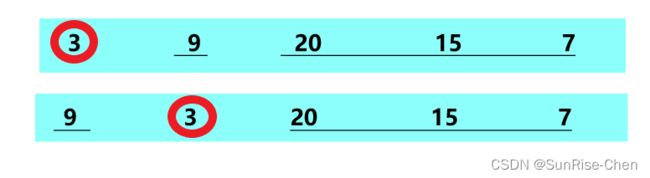
如图所例,根据前序遍历确定根节点,根据根节点在中序遍历中的位置确定左右子树的划分。之后递归,以划分的节点{9}为左子树,将9作为新的根节点进行构造,以节点{20,15,7}作为右子树构造右子树,以20作为右子树根节点,依此过程类推进行构造。
//该代码可在VS中进行测试,不是提交到leetcode代码
#include preorder;
//preorder.erase(preorder.begin()); 表示删除数组的首元素。
int root_t = preorder[0];
//preorder.erase(preorder.begin());
//把左子树的前序遍历和中序遍历从preorder和inorder中划分出来
//首先找到根节点在中序遍历中的位置
//ans为左子树元素个数
vector<int>::iterator iter;
iter = find(inorder.begin(), inorder.end(), root_t);
int ans = iter - inorder.begin();
//将左子树先序遍历的元素放入pre_l
//将左子树中序遍历的元素放入inorder_l;
//构建左子树
vector<int>pre_l;
vector<int>inorder_l;
pre_l.insert(pre_l.begin(), preorder.begin()+1, preorder.begin()+ans+1);
inorder_l.insert(inorder_l.begin(), inorder.begin(), iter);
tree->left = buildTree(pre_l, inorder_l);
//将右子树先序遍历的元素放入pre_r
//将右子树中序遍历的元素放入inorder_r;
//ans_r为右子树元素个数
//实际上Vector中的begin和end函数是左闭右开的区间,end为最后一个元素后移一位
int ans_r = inorder.end()-1-iter;
vector<int>pre_r;
vector<int>inorder_r;
pre_r.insert(pre_r.begin(), preorder.end()-ans_r, preorder.end());
inorder_r.insert(inorder_r.begin(),inorder.end()-ans_r, inorder.end());
tree->right = buildTree(pre_r, inorder_r);
return tree;
}
方法二:借助栈构造二叉树解题思路:
前序遍历中的任意两个连续节点 u 和 v,根据前序遍历,我们可以知道 u 和 v只有两种可能的关系:
(1)要么v 是 u 的左孩子。因为在遍历到 u 之后,下一个遍历的节点就是 u 的左孩子,即 v;
(2)u 没有左孩子,并且 v 是 u 或u的某个祖先节点的右孩子。如果 u没有左孩子,那么下一个遍历的节点就是 u 的右孩子(因为如果u有左孩子,则在前序遍历中v一定是其左孩子)。如果 u没有右孩子,我们就会向上回溯,直到遇到第一个有右孩子(且 u 不在它的右孩子的子树中)的节点 的右孩子,这也是前序遍历的顺序。
根据示例1解释这两种关系
Input: preorder = [3,9,20,15,7],
inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]
如上所示,依据preorder可以知道,对于连续的{3,9},9是3的左孩子,对于{9,20},20是9的祖先节点3的右孩子(9没有左孩子),对于{20,15},15是20的左子树,对于{15,7},15没有左子树,7是15的祖先节点的右子树。
1.我们用一个栈 stack 来维护前序遍历的节点,栈顶就是当前节点。同时,我们用一个指针 index 指向中序遍历的某个位置,初始值为 0。index 对应的节点是当前节点不断往左走达到的最终节点。
2.首先我们将根节点3 入栈,再初始化 index 所指向的节点为中序遍历首节点 9,随后对于前序遍历中的每个节点,若当前栈顶节点与当前index所指向的节点不相等,说明当前前序遍历节点为栈顶元素的左孩子,构建左孩子节点并将节点入栈。(试想,如果当前前序遍历节点即9不是栈顶节点3左孩子的话,那么按照前序遍历一定是节点3的右孩子,而若是右孩子的话,说明根节点没有左孩子,那么当前中序遍历index指向的元素一定是根节点本身3)。
3.当栈顶元素与当前index的值相等时,即9==9时,将栈顶元素9出栈,那么当前前序遍历的节点是9出栈后栈顶节点的右孩子或其祖先的右孩子,即20是元素3的右孩子,是当前出栈节点的祖先节点的右孩子(不一定是当前出栈节点的父节点,笼统的概括是祖先节点,因为当当前栈顶元素等于中序遍历时index指向的节点时,说明当前栈顶节点在前序遍历位置的左边节点已经构造完成,也说明当前栈顶节点无左孩子或它的左孩子无孩子,否则index指向的节点不会是当前栈顶节点,则当前前序遍历的节点是栈顶节点的右孩子或其祖先的右孩子)
4.当栈顶元素值=index值时,栈顶元素出栈后,index右移指向下一个位置元素,此时同样将更新后栈的栈顶元素与当前index指向的元素比较值,若相等则栈顶元素出栈,index指向中序遍历下一个元素,新的栈顶元素与index指向元素继续比较;若不相等则当前前序遍历到的节点为刚出栈的栈顶元素的右孩子,构建右孩子节点并将节点入栈。依此算法最终可以构造完成二叉树。
/*
用非递归方式构造给出前序遍历和后序遍历构造二叉树
*/
#include